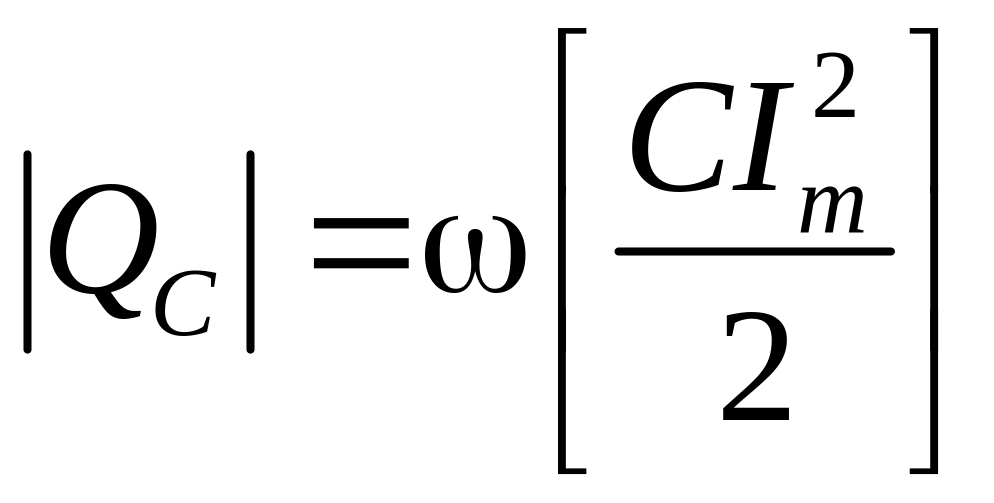1. Резистор

Ідеальний резистивный елемент не володіє ні індуктивністю, ні ємністю. Якщо до нього прикласти синусоїдальну напругу  (див. рис. 1), то струм i через нього дорівнює

.

(1)

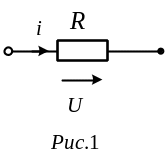
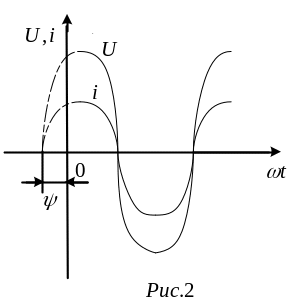
Співвідношення (1) показує, що струм має ту ж початкову фазу, що й напруга. Таким чином, якщо на вході двопроменевого осцилографа подати сигнали u й  i, то відповідні їм синусоїди на його екрані будуть проходити (див. рис. 2) через нуль одночасно, тобто на резисторі напруга й струм збігаються по фазі.

З (1) випливає:

, . 

 

    

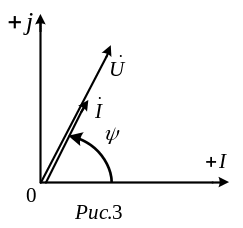
Переходячи від синусоїдальних функцій напруги й струму до відповідних їм комплексам:

;

,

– розділимо перший з виразыв на другий:

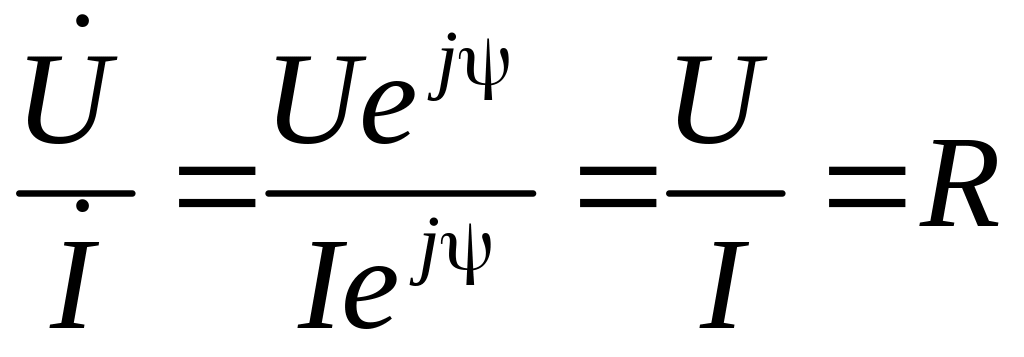
або

(2)

Отриманий результат показує, що відношення двох  комплексів є дійсна константа. Отже, відповідні їм вектори напруги й струму (див. рис. 3) збігаються за напрямком.

Миттєва потужність, яка надходить в ідальний резистивний елемент:

Тут напруга й струм (див. рис. 2) збігаються по фазі , тому потужність завжди позитивна, тобто резистор споживає активну потужність

2. Конденсатор

Ідеальний ємнісний елемент не має ні активного опіру (провідністю), ні індуктивністі. Якщо до нього прикласти синусоїдальну напругу  (див. рис. 4), то струм i  через нього буде дорівнює 

.

(3)

 

Отриманий результат показує, що напруга на конденсаторі відстає по фазі від струму на π/2. Таким чином, якщо на входи двопроменевого осцилографа подати сигнали u  й  i, то на його екрані буде мати місце картинка, що відповідає рис. 5.

З (3) випливає:

; . 

Введений параметр:

називають реактивним ємнісним опором конденсатора.

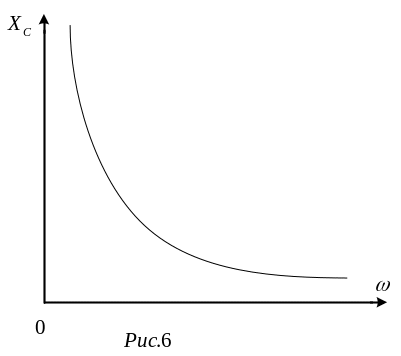
Як і резистивний опір, Х_С має розмірність Ом. Однак на відміну від R даний параметр є функцією частоти, що ілюструє рис. 6. З рис. 6 випливає, що при f=0 конденсатор представляє розрив для струму, а при .

Переходячи від синусоїдальних функцій напруги й струму до відповідним їм комплексам:

;

,

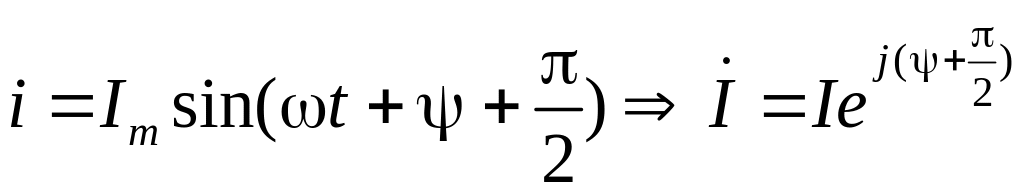– розділимо перший з виразів на другий:

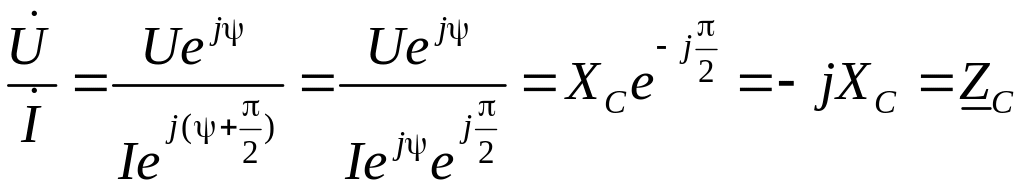
або

(4)

 

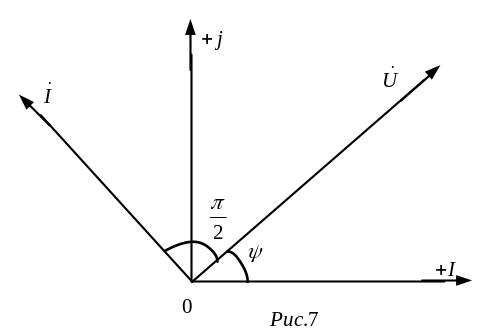
В останньому співвідношенні  – комплексний опір конденсатора. Множення на відповідає повороту вектора на кут π/2 по годинній стрілці. Отже, рівнянню (4) відповідає векторна діаграма, представлена на рис. 7.

Миттєва потужність, яка надходить в ідеальний конденсатор

Тут . Тому з (3) випливає, що . Таким чином, у конденсаторі (та котушці індуктивності) активна потужність не споживається (Р=0), тому що в них не відбувається необоротного перетворення енергії в інші види енергії. Тут відбувається тільки циркуляція енергії: електрична енергія запасається в магнітному полі котушки або електричному полі конденсатора протягом чверті періоду, а протягом наступної чверті періоду енергія знову повертається в мережу. У силу цього котушку індуктивності й конденсатор називають реактивними елементами, а їх опори і , на відміну від активного опору R резистора, – реактивними.

Интенсивність обміну енергії прийнято характеризувати найбільшим значенням швидкості надходження енергії в магнітне поле котушки або електричне поле конденсатора, що називається реактивною потужністю.

У загальному випадку вираз для реактивної потужності має вигляд:

 

Вона позитивна, якщо струм відстає (індуктивне навантаження – ) і негативне, якщо струм випереджає (ємнісне навантаження – ). Одиницю потужності в застосуванні до виміру реактивної потужності називають вольт-ампер реактивний (Вар).

З останнього видно, що реактивна потужність для ідеального конденсатора пропорційна частоті й максимальному запасу енергії в ній.