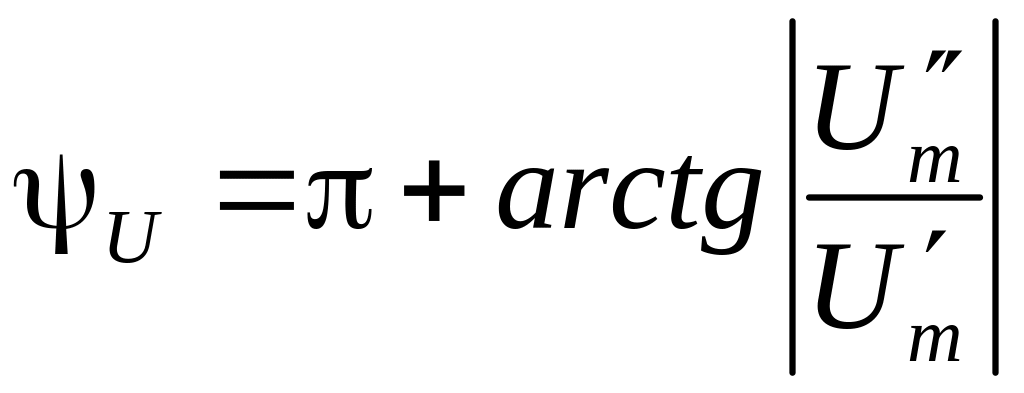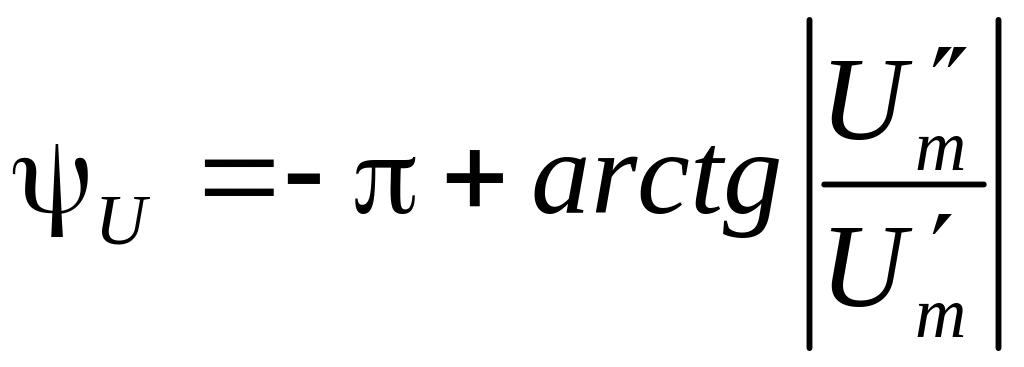- •Розділ 2 Лінійні електричні кола однофазного синусоїдного струму Вступ
- •Змінний струм. Зображення синусоїдних змінних
- •Синусоїдально змінний струм
- •Зображення синусоїдальних ерс, напруг і струмів на площині декартовых координат
- •Діюче значення змінного струму
- •Способи зображення синусоидально змінних величин
- •Векторне зображення синусоидально змінних величин
- •Подання синусоїдальних ерс, напруг і струмів комплексними числами
- •1. Резистор
- •2. Конденсатор
- •3. Котушка індуктивності
- •4. Послідовне сполучення резистивного й індуктивного елементів
- •5. Послідовна сполучення резистивного і ємнісного елементів
- •6. Паралельне сполучення резистивного і ємнісного елементів
- •7. Паралельне сполучення резистивного й індуктивного елементів
Подання синусоїдальних ерс, напруг і струмів комплексними числами
Геометричні операції з векторами можна замінити алгебраїчними операціями з комплексними числами, що істотно підвищує точність одержуваних результатів.
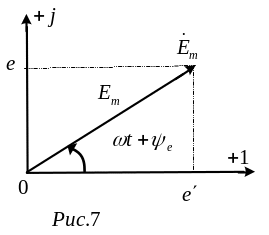
Коли
початок вектора сумістити з початком
координат комплексної площини(рис.7а),
то цей вектор можна записати комплексним
числом
![]() ,
де модуль комплексного числа дорівнює
довжині вектора, а аргумент вектора –
куту вектора з віссю дійсних значень.
,
де модуль комплексного числа дорівнює
довжині вектора, а аргумент вектора –
куту вектора з віссю дійсних значень.
Проекцією
вектора на вісь дійсних чисел наз.
дійсною частиною комплексного числа і
позначають
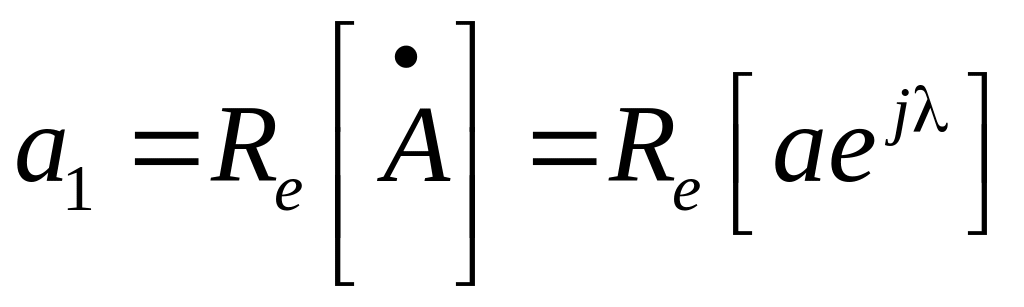 ,
проекцію на вісь умовних чисел – умовною
частиною і позначають
,
проекцію на вісь умовних чисел – умовною
частиною і позначають

Кожному вектору на комплексній площині відповідає певне комплексне число, що може бути записане в :
показниковій
![]()
тригонометричній ![]()
алгебраїчній ![]() –
формах.
–
формах.
Наприклад,
ЕРС
![]() ,
зображеної на рис. 7 обертовим вектором,
відповідає комплексне число
,
зображеної на рис. 7 обертовим вектором,
відповідає комплексне число
![]() .
.
Фазовий
кут![]() визначається
по проекціях вектора на осі “+1”
й “+j”
системи координат, як
визначається
по проекціях вектора на осі “+1”
й “+j”
системи координат, як
![]() .
.
Відповідно до тригонометричної форми запису уявна складова комплексного числа визначає миттєве значення синусоїдної змінної ЕРС:
|
(4) |
Комплексне
число![]() зручно
представити у вигляді добутку двох
комплексних чисел:
зручно
представити у вигляді добутку двох
комплексних чисел:
|
(5) |
Параметр![]() ,
що відповідає положенню вектора для
t=0
(або
на обертовій зі швидкістю
,
що відповідає положенню вектора для
t=0
(або
на обертовій зі швидкістю
![]() комплексної
площини), називають комплексною
амплітудою:
комплексної
площини), називають комплексною
амплітудою:![]() ,
а параметр
,
а параметр![]() комплексом
миттєвого значення.
комплексом
миттєвого значення.
Параметр
![]() є
оператором
повороту
вектора на кут
є
оператором
повороту
вектора на кут
![]() щодо
початкового положення вектора, при
розрахунках часто не враховується.
щодо
початкового положення вектора, при
розрахунках часто не враховується.
Загалом
кажучи, множення вектора на оператор
повороту![]() є
його поворот щодо первісного положення
на кут ±a.
є
його поворот щодо первісного положення
на кут ±a.
Отже, миттєве значення синусоїдальної величини дорівнює уявній частині без знака “j” добутку комплексу амплітуди й оператора повороту :
![]()
Перехід від однієї форми запису синусоїдальної величини до іншої здійснюється за допомогою формули Эйлера:
|
(6) |
Якщо, наприклад, комплексна амплітуда напруги задана у вигляді комплексного числа в алгебраїчній формі:
![]() ,
,
– то
для запису її в показовій формі, необхідно
знайти початкову фазу![]() ,
тобто кут, що утворить вектор
,
тобто кут, що утворить вектор![]() з
позитивною піввіссю +1:
з
позитивною піввіссю +1:
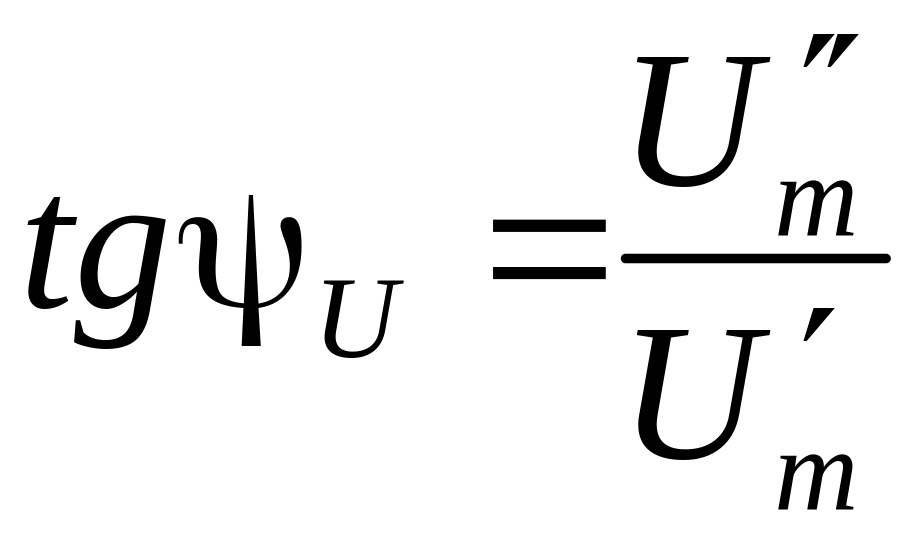
Тоді миттєве значення напруги:
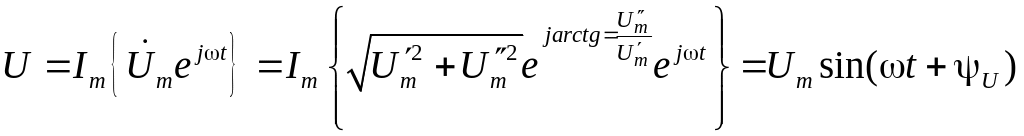
де
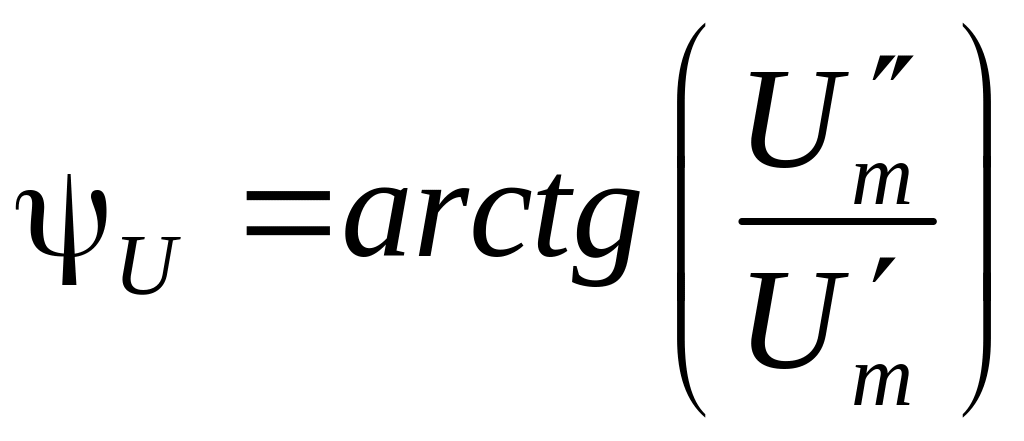
При
записі виразу для визначеності було
прийнято, що![]() ,
тобто що вектор зображення, перебуває
в першому або четвертому квадрантах.
Якщо
,
тобто що вектор зображення, перебуває
в першому або четвертому квадрантах.
Якщо![]() ,
то при
,
то при![]() (другий
квадрант)
(другий
квадрант)
|
(7) |
а
при
![]() (третій
квадрант)
(третій
квадрант)
|
(8) |
або
|
(9) |
Якщо
задано миттєве значення струму у вигляді
![]() ,
то комплексну амплітуду записують
спочатку в показовій формі, а потім (при
необхідності) по формулі Эйлера переходять
до алгебраїчної форми:
,
то комплексну амплітуду записують
спочатку в показовій формі, а потім (при
необхідності) по формулі Эйлера переходять
до алгебраїчної форми:
![]() .
.
Варто вказати, що при додаванні й вирахуванні комплексів варто користуватися алгебраїчною формою їхнього запису, а при множенні й розподілі зручна показова форма.
Отже, застосування комплексних чисел дозволяє перейти від геометричних операцій над векторами до алгебраїчного над комплексами. Так при визначенні комплексної амплітуди результуючого струму i3 по рис. 5 одержимо:
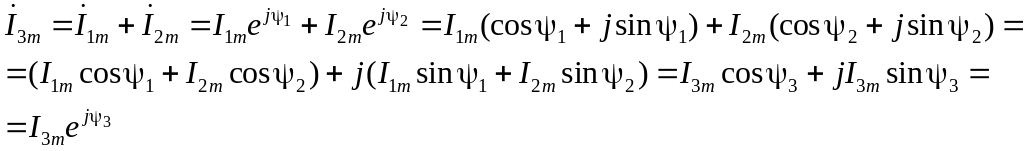 де
де![]() ;
;
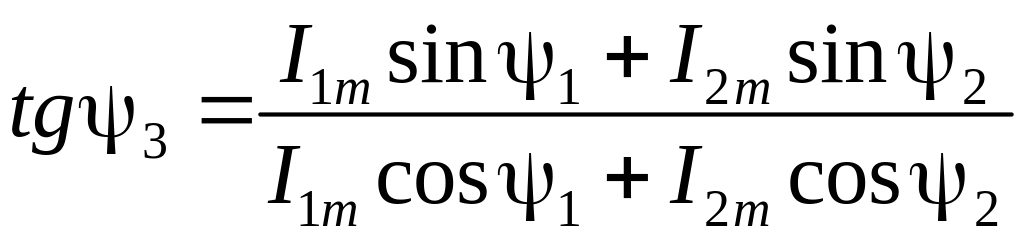 .
.
Лек №6
Елементи кола синусоїдного струму, векторні діаграми
та комплексні співвідношення для них

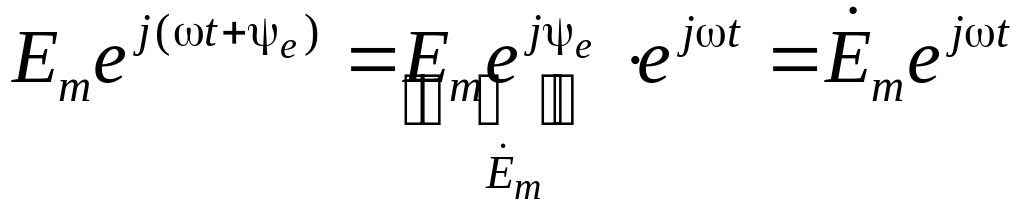
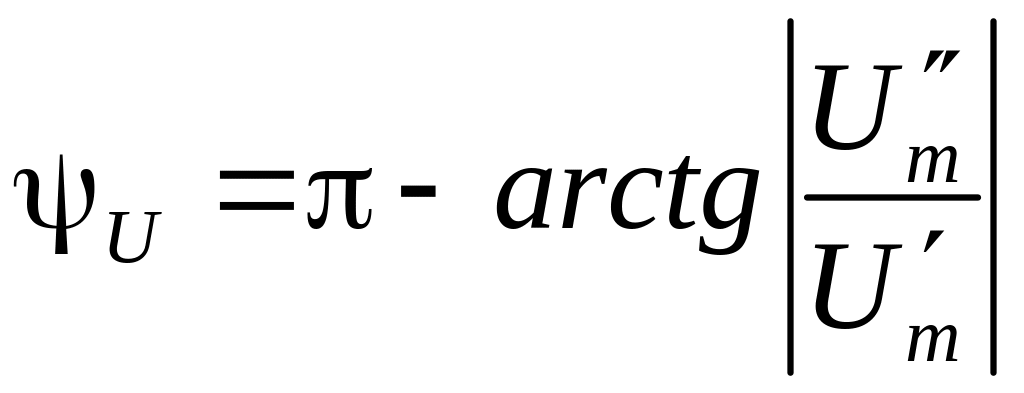 ,
,