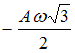- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
Решение:
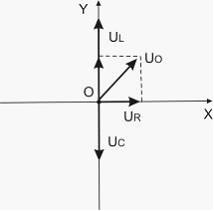 Используем
метод векторных диаграмм. Длина вектора
равна амплитудному значению напряжения,
а угол, который вектор составляет с осью
ОХ, равен фазе колебания напряжения
на соответствующем элементе. Сложив
три вектора, найдем амплитудное
значение полного напряжения:
Используем
метод векторных диаграмм. Длина вектора
равна амплитудному значению напряжения,
а угол, который вектор составляет с осью
ОХ, равен фазе колебания напряжения
на соответствующем элементе. Сложив
три вектора, найдем амплитудное
значение полного напряжения: ![]() .
Величина
.
Величина
![]() .
Полное сопротивление контура найдем
по закону Ома:
.
Полное сопротивление контура найдем
по закону Ома: 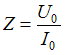 ,
где
,
где
![]() амплитудные
значения напряжения и силы тока.
Амплитудное значение силы тока указано
в законе изменения силы тока и равно
0,1 А.
амплитудные
значения напряжения и силы тока.
Амплитудное значение силы тока указано
в законе изменения силы тока и равно
0,1 А. 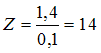 Ом.
Ом.
69.
Плоская
звуковая волна
![]() распространяется
в упругой среде. Скорость колебания
частиц среды, отстоящих от источника
на расстоянии
распространяется
в упругой среде. Скорость колебания
частиц среды, отстоящих от источника
на расстоянии
![]() ,
в момент времени
,
в момент времени
![]() равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Скорость
колебания частиц среды равна:
![]() ,
где
–
амплитуда волны;
,
где
–
амплитуда волны;
![]() –
циклическая частота волны;
–
период колебаний;
–
циклическая частота волны;
–
период колебаний;
![]() –
волновое число;
–
длина волны; (
–
волновое число;
–
длина волны; (![]() )
– фаза волны. Скорость частиц среды,
находящихся от источника на расстоянии
,
в момент времени
равна
)
– фаза волны. Скорость частиц среды,
находящихся от источника на расстоянии
,
в момент времени
равна
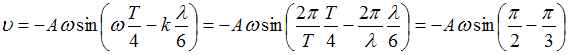 .
Следовательно,
.
Следовательно,
![]() .
.
70.
В упругой среде плотности распространяется плоская синусоидальная волна с частотой и амплитудой . Если частоту увеличить в 4 раза, а амплитуду уменьшить в 2 раза, объемная плотность энергии …
|
|
уменьшится в 2 раза |
|
|
увеличится в 64 раза |
|
|
увеличится в 4 раза |
|
|
увеличится в 2 раза |
Решение:
Среднее значение объемной плотности энергии равно . За счет увеличения частоты объемная плотность энергии увеличится в 16 раз, а за счет уменьшения амплитуды – уменьшится в 4 раза, следовательно, объемная плотность энергии увеличится в 4 раза.
71.
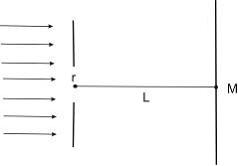
На
диафрагму с круглым отверстием радиусом
1 мм падает нормально параллельный
пучок света длиной волны 0,5 мкм. На пути
лучей, прошедших через отверстие, на
расстоянии 1 м помещают экран. В центре
экрана в точке М будет наблюдаться …
|
|
светлое пятно, так как в отверстии укладываются 3 зоны Френеля
|
|
|
светлое пятно, так как в отверстии укладываются 5 зон Френеля
|
|
|
темное пятно, так как в отверстии укладываются 4 зоны Френеля
|
|
|
темное пятно, так как в отверстии укладываются 2 зоны Френеля |
Решение:
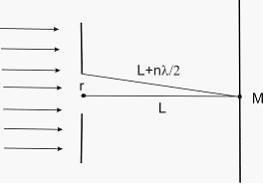 Определим,
сколько зон Френеля укладывается в
отверстие диафрагмы радиуса
Определим,
сколько зон Френеля укладывается в
отверстие диафрагмы радиуса
![]() .
Расстояния от соседних зон Френеля до
точки наблюдения М должны отличаться
на
.
Расстояния от соседних зон Френеля до
точки наблюдения М должны отличаться
на
![]() .
Следовательно, расстояние от точки М
до крайней точки отверстия будет равно
.
Следовательно, расстояние от точки М
до крайней точки отверстия будет равно
![]() ,
где
–
расстояние от диафрагмы до экрана,
–
число зон Френеля,
–
длина волны света. Воспользуемся теоремой
Пифагора:
,
где
–
расстояние от диафрагмы до экрана,
–
число зон Френеля,
–
длина волны света. Воспользуемся теоремой
Пифагора:
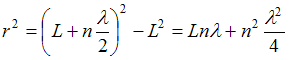 .
Учтем, что
.
Учтем, что
![]() –
величина второго порядка малости по
сравнению с
,
и пренебрежем слагаемым
–
величина второго порядка малости по
сравнению с
,
и пренебрежем слагаемым
![]() .
Тогда
.
Тогда
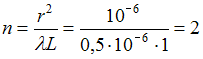 .
В отверстии диафрагмы укладываются 2
зоны Френеля, четное число; следовательно,
в центре экрана будет наблюдаться темное
пятно.
.
В отверстии диафрагмы укладываются 2
зоны Френеля, четное число; следовательно,
в центре экрана будет наблюдаться темное
пятно.
72.
На пути естественного света помещены две пластинки турмалина. После прохождения пластинки 1 свет полностью поляризован. Если и – интенсивности света, прошедшего пластинки 1 и 2 соответственно, и угол между направлениями оптических осей OO и O’O’ , то и связаны соотношением …
|
|
|
|
|
|
|
|
|
|
|
|