Решение:

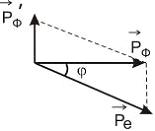
При рассеянии фотона на свободном электроне выполняются законы сохранения импульса и энергии. По закону сохранения импульса, = , где  – импульс фотона до рассеяния,  – импульс фотона после рассеяния,    – импульс электрона отдачи. Из рисунка видно, что 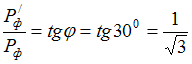. Следовательно, после рассеяния импульс фотона уменьшится в  раз.

54.

На рисунке изображена схема энергетических уровней атома водорода. Показаны состояния с различными значениями орбитального квантового числа. 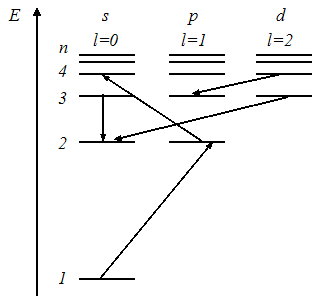Запрещенными правилом отбора для орбитального квантового числа являются переходы …

Решение:

Для орбитального квантового числа l имеется правило отбора . Это означает, что возможны только такие переходы, в которых l изменяется на единицу. Поэтому запрещены переходы: , где орбитальное квантовое число l не изменяется, и , где .

55.

Положение бусинки массы  1 г и положение электрона ( кг) определены с одинаковой погрешностью м. Если квантовомеханическая неопределенность x-компоненты  скорости бусинки составляет примерно , то для электрона неопределенность  равна …

		м/с
		м/с
		м/с
		м/с

Решение:

Из соотношения неопределенностей Гейзенберга для координаты и соответствующей компоненты импульса следует, что , где  – неопределенность координаты,  – неопределенность x-компоненты импульса,  – неопределенность x-компоненты скорости,  – масса частицы;  – постоянная Планка, деленная на . Неопределенность x-компоненты скорости можно найти из соотношения . Следовательно, для бусинки и электрона можно записать следующее выражение: 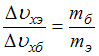, откуда .

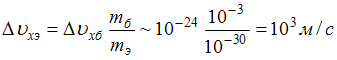56.

Стационарное уравнение Шредингера имеет вид 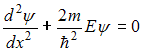. Это уравнение записано для …

		частицы в одномерном потенциальном ящике с бесконечно высокими стенками
		частицы в трехмерном потенциальном ящике с бесконечно высокими стенками
		линейного гармонического осциллятора
		электрона в атоме водорода

Решение

Стационарное уравнение Шредингера в общем случае имеет вид 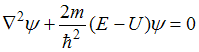, где U – потенциальная энергия микрочастицы. Для одномерного случая 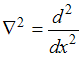. Кроме того, внутри потенциального ящика U = 0, а вне ящика частица находиться не может, т.к. его стенки бесконечно высоки. Поэтому данное уравнение Шредингера записано для частицы в одномерном ящике с бесконечно высокими стенками.

57.

Если -функция электрона в одномерном потенциальном ящике шириной L с бесконечно высокими стенками имеет вид, указанный на рисунке, то вероятность обнаружить электрон на участке  равна …