ТЕСТЫ

1.

Прямолинейное движение точки описывается уравнением       (в единицах СИ). Средняя скорость точки за время движения до остановки в  равна

Введите ответ:

Решение:

Найдем скорость: . При        . Следовательно, время движения до остановки равно . Средняя скорость за время движения до остановки   . Ответ:   .

2.

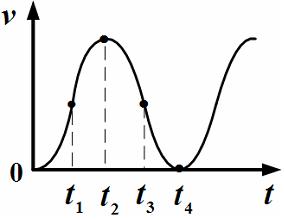
Модуль скорости автомобиля изменялся cо временем, как показано на графике зависимости   . В момент времени  автомобиль поднимался по участку дуги.  

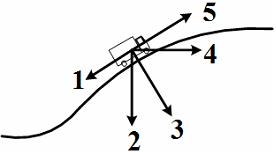
Направление результирующей всех сил, действующих на автомобиль в этот момент времени, правильно отображает вектор …

Решение В системе отсчета, связанной с Землей, ускорение автомобиля    и результирующая действующих на него сил  связаны вторым законом Ньютона: 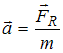 и . Полное ускорение ,  – тангенциальная составляющая ускорения,  – нормальная составляющая ускорения. Как следует из графика зависимости модуля скорости от времени, в момент  модуль скорость автомобиля достигает максимального значения  и . Поскольку автомобиль движется в этот момент по криволинейному участку траектории, то . Следовательно,  (см. рисунок) и ее направление совпадает с направлением вектора 3. Ответ: вектор 3.

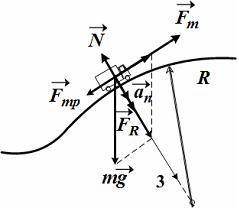
3.

На барабан радиусом  намотан шнур, к концу которого привязан груз массой  Груз опускается с ускорением   . Момент инерции барабана равен …

Введите ответ:

Решение:

Запишем уравнение движения груза    , где    сила натяжения шнура, под действием которой также происходит вращение барабана. Уравнение вращения барабана: . Ускорение поступательного движения груза совпадает с линейным ускорением точек на поверхности барабана, поэтому ускорение груза и угловое ускорение барабана  связаны соотношением . Из этих уравнений найдем . Подставляя числовые значения, получим .

4.

Тело движется вдоль оси под действием силы, зависимость которой от координаты  представлена на рисунке: 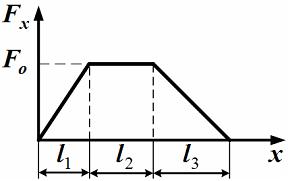Работа силы на пути  определяется выражением …

Решение:

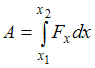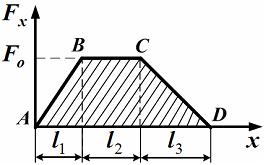
Работа переменной силы в случае одномерного движения  на участке  определяется как интеграл: .  На графике зависимости силы от координаты искомая работа представлена площадью, ограниченной кривой зависимости и осью координат (геометрический смысл интеграла). Следовательно, искомая работа численно равна площади трапеции ABCD, то есть произведению полусуммы оснований на высоту: .

5.

Шар и полая сфера, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Если начальные скорости этих тел одинаковы, то …

		выше поднимется шар
		оба тела поднимутся на одну и ту же высоту
		высоту подъема тел невозможно определить
		выше поднимется полая сфера

Решение:

Воспользуемся законом сохранения механической энергии. Полная энергия тел не изменяется, поэтому . Здесь 1 и 2 – состояния системы,  – потенциальная энергия тела, причем , и кинетическая энергия плоского движения твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения вокруг оси, проходящей через центр масс: . В последней формуле  – момент инерции тела относительно оси, проходящий через его центр масс;  – скорость его центра масс. Из условия отсутствия проскальзывания следует, что мгновенные скорости точек касания тела о горку равны нулю, то есть угловая скорость . В нашем случае, энергии тела в первом и во втором состояниях равны: . Из закона сохранения энергии 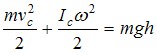 следует  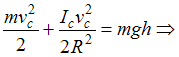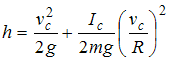 . Анализируя последнюю формулу, видим, что при равенстве масс, скоростей, радиусов однородного шара и полой сферы . Сравним моменты инерции тел, обозначив их у шара , у полой сферы – . Момент инерции I – величина, характеризующая распределение массы тела относительно оси вращения и являющаяся мерой инертности тела при вращательном движении. Вся масса полой сферы находится на расстоянии  от оси вращения, а у шара распределена равномерно вдоль радиуса сферы. Тогда < , следовательно, . Значит, полая сфера поднимется на горку выше, чем однородный шар.

6.

Если масса тела возросла на 1 г, полная энергия тела должна …

		уменьшиться на
		увеличиться на
		увеличиться на
		увеличиться на

Решение:

Связь между массой и энергией определяется формулой Эйнштейна , где – скорость света. Следовательно, энергия тела должна возрасти на .

7.

На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от  до  в расчете на единицу этого интервала. Для этой функции является верным утверждение, что …

		с уменьшением температуры величина максимума функции уменьшается
		с увеличением температуры величина максимума функции увеличивается
		при изменении температуры положение максимума не изменяется
		при изменении температуры площадь под кривой не изменяется

Решение:

Полная вероятность равна: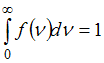 , т.е. площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры  не изменяется. Из формулы наиболее вероятной скорости 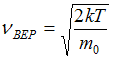, при которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо.

8.

Если количество теплоты, отдаваемое рабочим телом холодильнику, увеличится в два раза, то коэффициент полезного действия тепловой машины …

		уменьшится на
		увеличится на
		уменьшится на
		увеличится на