
- •1. Простые, сложные, непрерывные проценты
- •Задачи с решениями
- •Задачи для самостоятельного решения
- •2. Поток платежей
- •Задачи с решениями
- •Вопрос 1: построить поток платежей для указанных условий.
- •Вопрос 2: пользуясь пакетом ms Excel, рассчитать годовой irr полученного потока платежей.
- •Задачи для самостоятельного решения
- •Вопрос 1: Найти npv.
- •Вопрос 2: Необходимо рассчитать irr вложения в акции железнодорожной компании.
- •3. Дюрация потока платежей
- •Задачи с решениями
- •Задачи для самостоятельного решения
- •4. Теория портфеля. Задача г. Марковица
- •Задачи с решениями
- •Задачи для самостоятельного решения
- •5. Задача Дж. Тобина и теория идеального
- •Решение задачи Тобина. Линия рынка (смl)
- •Модель ценообразования на рынке капитала (Capital Asset Pricing Model – capm)
- •Диверсифицируемый (устранимый, не систематический) и не диверсифицируемый (систематический) риск
- •Задачи с решениями
- •Задачи для самостоятельного решения
- •6. Введение в теорию опционов
- •Задачи с решениями
- •Задачи для самостоятельного решения
- •Основная литература
- •Дополнительная литература
- •620002, Г. Екатеринбург, ул. Мира, 19
3. Дюрация потока платежей
Вычислим
производную приведенной стоимости
потока платежей
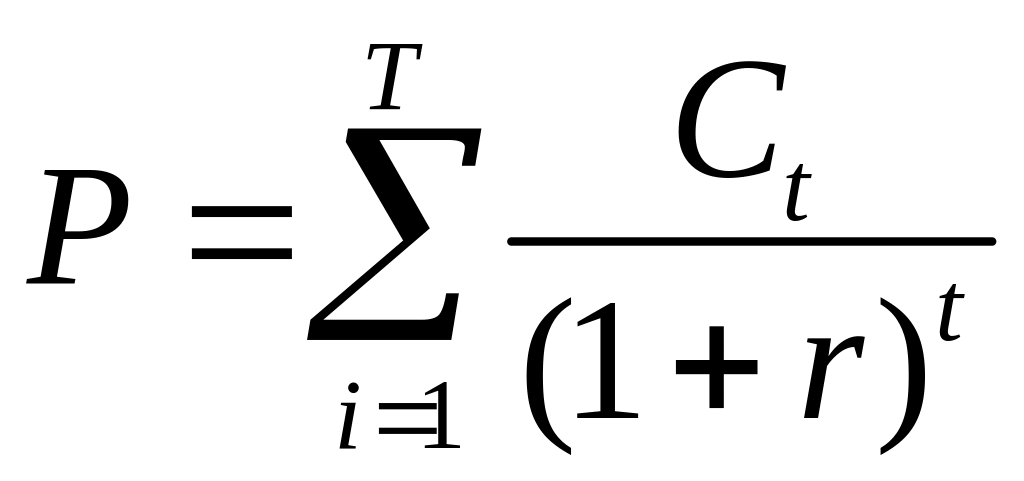 :
:
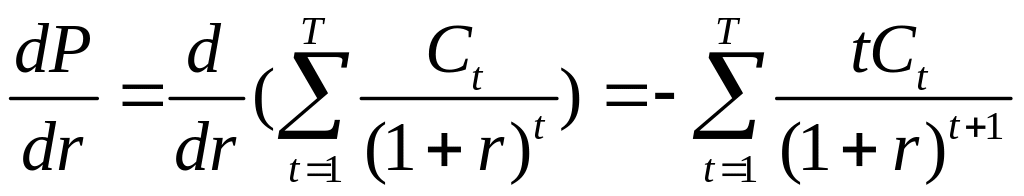 .
.
Разделим обе части
равенства на
![]() и умножим на
и умножим на
![]() :
:
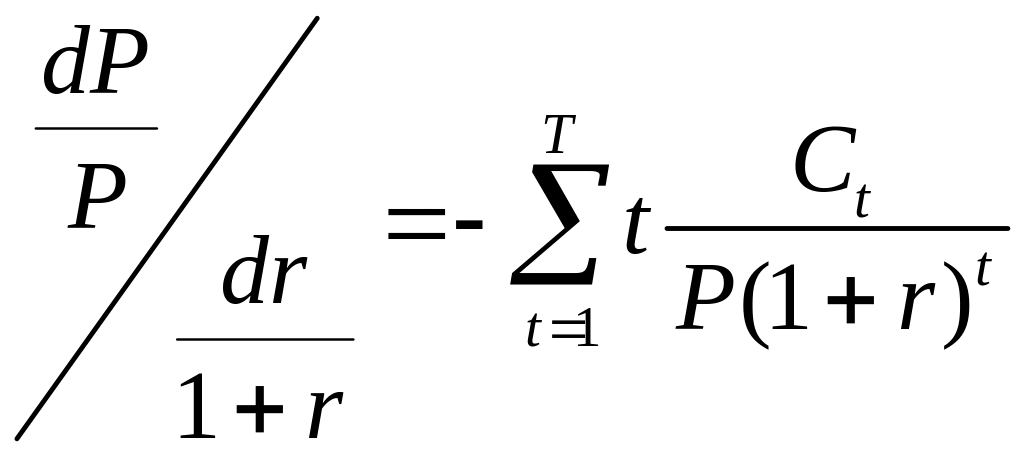 ,
или
,
или
 ,
,
где
 .
.
Дюрацией потока платежей называется величина
 .
.
Cмысл и свойства дюрации:
1. Дюрация – эластичность приведенной стоимости относительно изменения процентной ставки.
2. Дюрация – средняя продолжительность потока платежей.
![]() ,
,
![]()
Если поток состоит из единственного платежа, осуществляемого в момент t=t*
( Ct
= 0
при
![]() ),
то
),
то
![]() .
.
Задачи с решениями
Задача 3.1
Через 2 года необходимо покрыть долг в размере $1 000. На рынке имеются облигации со сроком погашения через 1 год (А) и через 3 года (Б). Облигации А погашаются по $7, Б – по $10. Процентная ставка r0 = 10%.
Вопрос: Рассчитать количество облигаций А и Б, необходимых для покрытия долга, а так же для хеджирования риска изменения процентной ставки.
Решение.
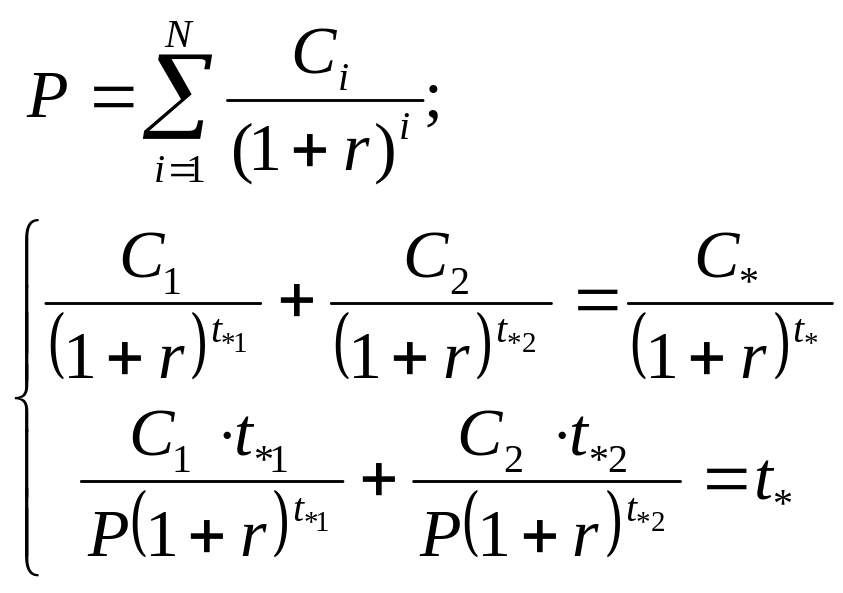 ,
где
,
где
C1 – количество облигаций типа А, С2 – количество облигаций типа Б, необходимых для хеджирования риска изменения процентной ставки; t*1 – момент погашения облигации А, t*2 – момент погашения облигации Б, С* - долг, t* - момент погашения долга.
Подставим значения:

С1 = 455, С2 = 550,
Стоимость облигаций А – 7$, следовательно их необходимо 65 штук, стоимость облигаций Б – 10$, следовательно их необходимо 55 штук.
Ответ: необходимо 65 облигаций А и 55 облигаций Б.
Задачи для самостоятельного решения
Задача 3.2
Пусть
![]() .
Инвестор имеет долг
.
Инвестор имеет долг
![]() .
Есть возможность купить облигации двух
видов:
.
Есть возможность купить облигации двух
видов:
а) с выплатой при
![]() и номиналом
и номиналом
![]() ;
;
б) с выплатой при
![]() и номиналом
и номиналом
![]() .
.
Безрисковая процентная
ставка
![]() .
.
Вопрос: сколько облигаций а) и б) нужно иметь, чтобы купировать долг и хеджировать риск изменения процентной ставки?
4. Теория портфеля. Задача г. Марковица
Предполагается, что
имеется N рисковых
активов (ценных бумаг, акций). Доходность
отдельного актива (ценной бумаги)
трактуется как случайная величина –
![]() .
.
Ожидаемая доходность
определяется как математическое ожидание
–
![]() ,
вектор доходностей –
,
вектор доходностей –
![]() .
.
Риск, связанный
с отдельной бумагой формализуется как
среднеквадратичное отклонение –
![]() .
.
Инвестиционный портфель:
![]() –
вектор долей капитала:
–
вектор долей капитала:
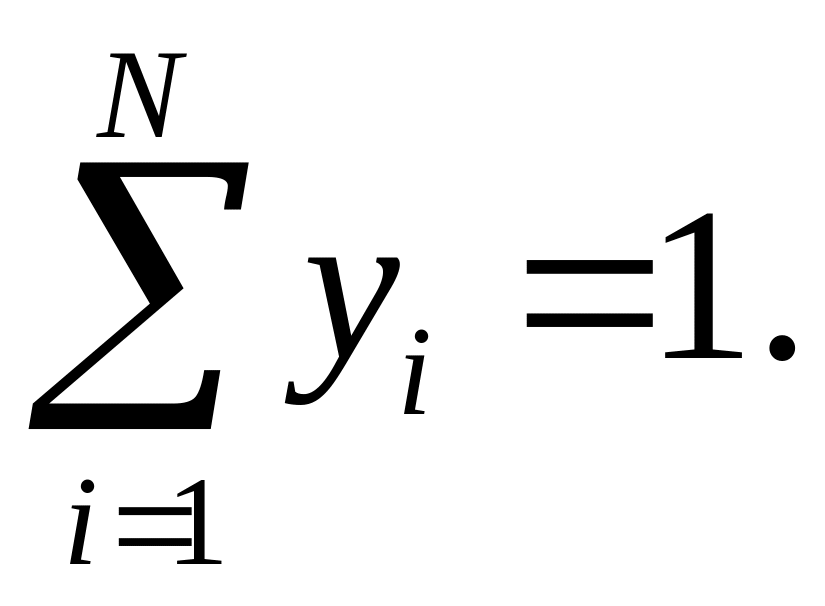
Случайная доходность портфеля определяется соотношением
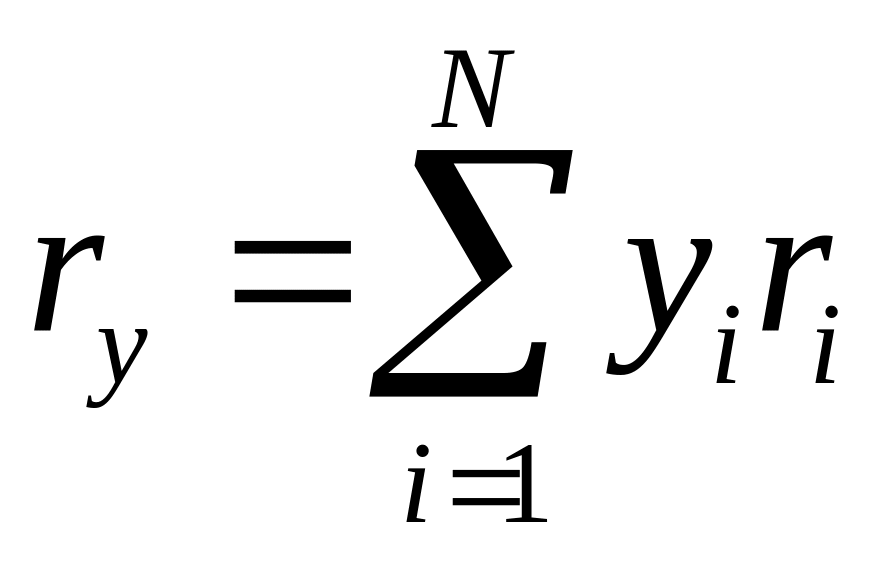
Риск портфеля:
 ,
,
![]()
Доходность портфеля:
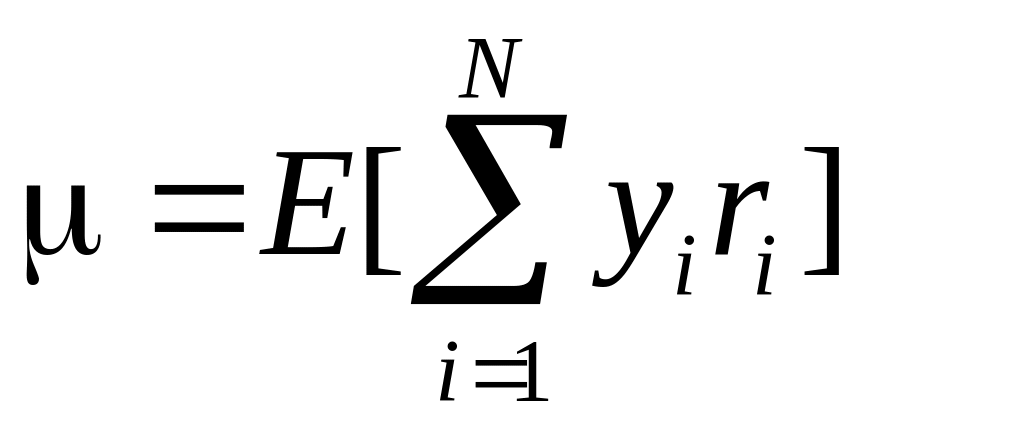 .
.
Задача
Марковица:
![]() (найти минимум)
при ограничениях:
(найти минимум)
при ограничениях:
![]()
![]()
Учитывая,
что
 задачу можно записать в виде:
задачу можно записать в виде:
![]()
![]() ,
,
![]() ,
,
где
![]()
Задачи с решениями
Задача 4.1
Решить задачу Марковица
для случая двух рисковых активов, при
заданных
![]() и
и
![]() - ожидаемых значениях доходностей,
дисперсиях
- ожидаемых значениях доходностей,
дисперсиях
![]() и
и
![]() и
и
![]() - коэффициенте корреляции случайных
доходностей активов.
- коэффициенте корреляции случайных
доходностей активов.
Решение.
Рассмотрим задачу Марковица
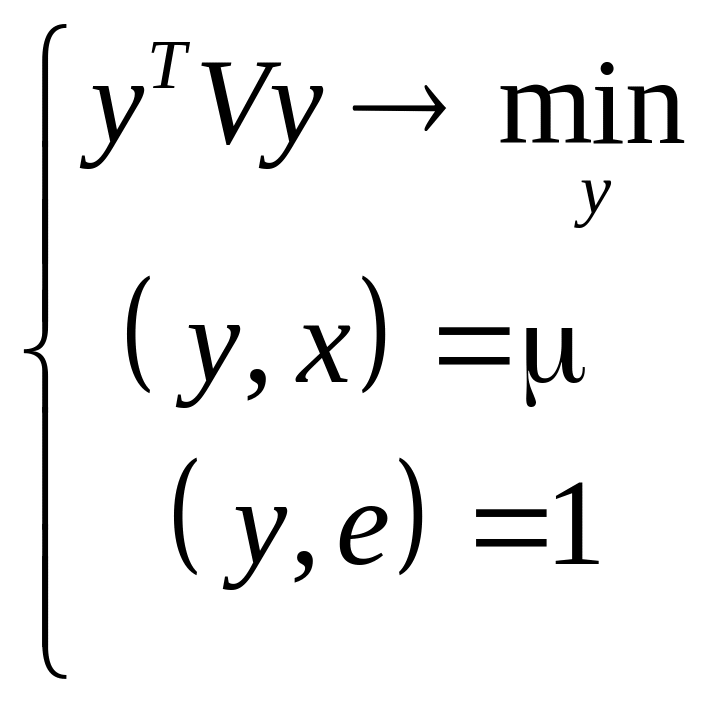
для
случая, когда вектор
![]() имеет
размерность, равную 2; матрица
имеет
размерность, равную 2; матрица
![]() -
-
![]() .
.
Для двух рисковых активов имеем:
 .
.
Расписывая первое соотношение задачи подробнее, получим:
![]() ,
,
где

С учетом приведенных соотношений задача записывается в виде
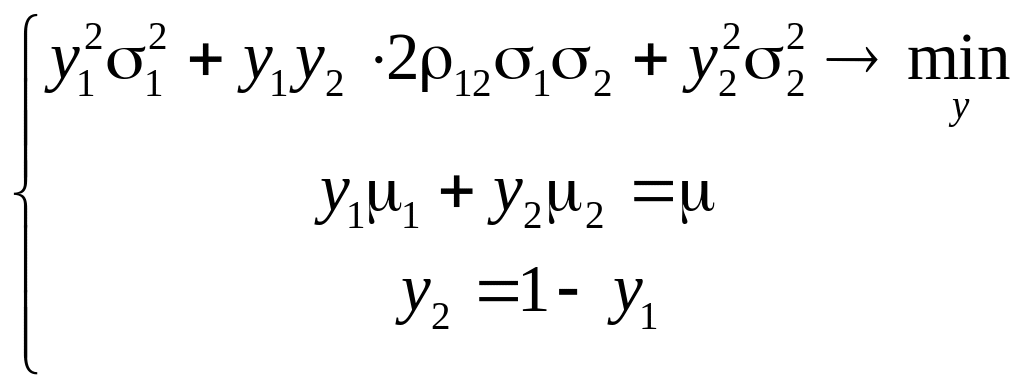
или
 (4.1)
(4.1)
Поскольку число
ограничений равно числу переменных,
задача на поиск минимума вырождается.
Предполагая, что
![]() ,
из второго равенства в (4.1) выражаем
,
из второго равенства в (4.1) выражаем
 и, подставляя в первое соотношение,
находим связь между параметрами
и, подставляя в первое соотношение,
находим связь между параметрами
![]() и
и
![]() для решений задачи Марковица в
рассматриваемом случае.
для решений задачи Марковица в
рассматриваемом случае.
 .
.
Функция, стоящая в
правой части равенства, может быть
приведена к виду
![]() ,
где
,
где
![]() ,
,
![]() .
Если последние неравенства – строгие,
то
.
Если последние неравенства – строгие,
то
![]() ,
и значения риска
,
и значения риска
![]() может быть определено для всех значениях
может быть определено для всех значениях
![]() .
.
Портфель y называется эффективным (не улучшаемым, Парето-оптимальным), если не существует такого портфеля y* , что μ(y*) ≥ μ(y) и σ(y*) ≤ σ(y), причем одно из неравенств – строгое.

Рис. 4.1 Эффективные портфели рисковых инвестиций
