4. Сферические треугольники в задачах судовождении

Решение параллактических треугольников

Сферический треугольник на небесной сфере, вершинами которого являются повышенный полюс мира — Р, зенит наблюдателя— Z и светило — С называется параллактическим треугольником (рис. 4.1).

Углы параллактического треугольника:

t — часовой угол при вершине Р ;

А - азимут при вершине Z;

q - параллактический угол при светиле С.

Стороны параллактического треугольника:

90°-φ-сторона между вершинами Р и Z;

φ-широта места;

90° -δ- сторона между вершинами Р и С;

δ- склонение светила;

90°-h- сторона между вершинами Z и С.

h - высота светил.

При решении параллактического треугольника будем считать заданными φ - широту места, δ и t - координаты светила в экваториальной системе. Определим h и А - координаты светила в горизонтной системе.

Наиболее универсальными и удобными для расчетов на микрокалькуляторе являются формулы:

sin h = sin φ sin δ + cos φ cos δ cos t (4.1)

tg A = sin t / (cos φ tg δ - sin φ cos t) (4.2)

Формулу (4.1) получили, применив теорему косинус стороны для элемента 90°-h параллактического треугольника, а формулу (4.2) -теорему котангенсов для четырех рядом лежащих элементов А, 90°-φ,t,90°-δ (рис.4.1).

Аргументы φ, δ, t имеют наименования, поэтому при решении им

приписываются знаки:

(φ u t - всегда знак "+";

δ - знак "+", если одноименно с φ ,

знак "-", если разноименно с φ.

Примечания.

1. Главное значение функции arctg находится в интервале от -90° до +90°. Поэтому, если полученное по формуле (4.2) значение А отрицательное, необходимо к результату прибавить 180°.

2. Азимут А получаем в полукруговом счете. Первая буква его наименования одноименна с φ, вторая - одноименна с t.

3. В ответе h записываем в градусах, минутах и десятых доля минуты, А переводим в круговой счет и записываем с точностью до 0,1°.

Пример 4.1 Заданы следующие значения (φ = 58°10,7'S;

δ = 21°40,5'S; t= 10°13,7'W. Решить параллактический треугольник, вычислить h, A.

Решение.

1. Исходные данные:

φ = 58°10,7'S = +58,178°;

δ= 21°40,5'S = +21,675°;

t= 10°13,7'W=+10,228°.

2. Подставляем значения аргументов в формулы (4.1) и (4.2) и рассчитываем значения h и А:

h = 52,753° = 52°45,2';

А = -15,8° т.к. А<0 → А = A+180°= 164,2°;

3. Даем азимуту наименование, переводим в круговой счет:

А = S 164,2° W = 344,2°.

Ответ: h = 52°45,2'; А = 344,2°.

В задачах №№ 271- 300 решить параллактический треугольник, найти h и А.

№	φ		δ		t
271	58° 48,6'	N	56°07,5'	N	105° 44,1' W
272	41 25.1	N	10 15.3	N	70 14.8 E
273	36 10.5	S	14 15.1	S	60 13.7 W
274	68 20.5	N	4 16.2	S	10 13.9 E
275	24 10.7	N	12 52.1	N	25 37.3 W
276	70 20.1	N	11 15.4	N	35 45.1 E
277	0 02.5	S	24 31.5	S	41 12.6 W
278	23 27.1	N	14 35.4	S	20 45.7 E
279	34 21.5	S	55 10.4	S	81 30.7 W
280	50 45.3	S	57 23.5	S	110 23.6 E
281	17 58.6	N	23 45.7	S	10 56.1 W
282	2 50.5	N	48 13.7	S	75 13.4 E
283	21 59.5	N	60 48.3	N	101 13.6 E
284	12 40.2	S	21 22.4	N	45 32.7 W
285	18 29.1	N	27 13.4	S	15 57.3 E
286	21 35.6	S	22 14.9	S	5 32.7 W
287	11 12.5	S	18 33.8	S	87 14.6 E
288	51 10.4	N	13 52.8	N	40 52.7 W
289	44 28.5	N	64 13.6	N	100 45.3 E
290	37 30.3	N	64 13.6	N	100 45.3 E
291	29 38.5	S	55 23.4	S	73 43.7 E
292	36 15.5	S	8 30.4	N	22 56.1 W
293	58 49.5	N	60 25.3	N	102 53.1 E
294	22 40.6	S	17 33.4	N	51 35.7 W
295	11 18.7	N	33 57.4	N	6125.7 E
296	68 23.6	N	56 21.7	N	124 50.8 W
297	47 46.7	S	55 13.4	S	12 54.1 E
298	12 15.5	N	25 46.8	S	22 36.4 W
299	56 15.2	N	55 45.7	N	110 32.7 E
300	26,35.4	S	18,45.1	N	55,23.6 W

Расчет плавания по локсодромии и ортодромии

Плавание между двумя точками 1 и 2 с координатами φ₁; λ₁ и φ₂; λ₂ можно совершить двумя путями: по локсодромии (постоянным курсом, но более длинным путем) и по ортодромии (кратчайшим путем, но переменными курсами). Разница в длине пути будет существенной при плавании на большие расстояния (трансокеанские переходы) и при близких значениях широт точек 1 и 2. Локсодромия и ортодромия совпадают при курсах, близких к 0° и 180°, а также на любых курсах вблизи экватора. Будем решать задачу на сфере (без учета сфероидичности Земли).

Задача расчета плавания по локсодромии состоит в определении локсодромического курса К._л и длины локсодромии S_Л.

Рис.4.2 выполнен на карте меркаторской проекции. Следовательно, треугольник 012 является плоским прямоугольным треугольником. Гипотенуза 12 - локсодромическое плавание в морских милях, катет 01 -разность долгот в экваториальных милях, катет 02 -разность широт в морских милях и разность меридиональных частей в экваториальных милях. Угол при вершине 2 равен К_л .При выполнении расчетов северная широта, разность широт, восточная долгота и разность долгот считаются положительными, а южная широта, разность широт, западная долгота и разность долгот -отрицательными. Алгоритм решения данной задачи включает следующие действия:

1. Вычисление разности широт РШ

PШ = φ₂-φ₁.

Полученное значение РШ переводим в угловые минуты (морские мили).

2.Определение разности долгот РД

РД=λ₂- λ₁.

Если | λ₂- λ₁ | > 180°, то при вычислении РД берется дополнение абсолютной величины до 360°, знак меняется на противоположный. Полученное значение РД переводим в угловые минуты (экваториальные мили).

3. Расчет разности меридиональных частей РМЧ в экваториальных милях

РМЧ = 3437,75 * ln[tg (45° + <φ₂/2) / tg (45 °+ φ₁/2)].

Примечание: Знаки РШ и РМЧ должны совпадать.

4. Определение локсодромического курса К_л

К_л' = arccos ( РМЧ/); при РД > 0 К_л = К_л'; (4.3)

при РД < О К_Л = 360° - К_л'.

5. Расчет локсодромического расстояния S_л (в морских милях)

при | cosК_л, | ≥ 0,01 S_л = РШ/ cosК_л; (4.4)

при | cosК_л | < 0,01 S_л= | РД| cos φ₁ . (4.5)

Курс судна задается рулевому и учитывается при прокладке на карте с точностью до 0,5°, но при вычислении локсодромического расстояния необходимо использовать значение К_л с точностью не ниже 0,001° (практически берем то значение К_л, которое появилось на индикаторе микрокалькулятора после вычисления по формуле (4.3).

При решении задачи плавания по ортодромии ограничимся расчетом D_o— длины ортодромии и К_н- начального курса плавания по ортодромии.

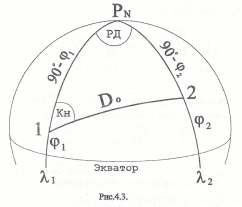
Треугольник с вершинами 1,2,P_N (рис.4.3) - сферический, Заданными элементами являются две стороны 90°-φ₁ , 90°-φ₂ и угол между ними РД. Сторону D₀ определим, использовав теорему косинус стороны. Угол Кн — начальный курс рассчитаем, применив теорему котангенсов для четырех рядом лежащих элементов - К_н, 90°- φ₁, РД, 90°-φ₂.

cos D₀ = cos(90°-φ₁) cos(90°-φ₂) + sin(90°- φ₁) sin(90°-φ₂) cos РД; (4.6)

ctg K_H sin РД = ctg(90°-φ₂) sin(90°- φ₁) - cos(90°- φ₁) cos РД. (4.7)

Пример 4.2 Даны координаты двух точек в Тихом океане:

п. Сан-Франсиско 1 (φ₁= 37°40'N, , λ₁ = 124°30'W)

о-в Хокайдо 2 (φ₂= 42°30'N, λ₂= 143°20'Е).

Рассчитать курс и плавание по локсодромии; длину пути и начальный курс плавания по ортодромии.

Решение:

1. Исходные данные:

φ₁=37°40'N = +37,67°; φ₂= 42°30' N = +42,50°;

λ₁ = 124°30' W = -124,50°; λ₂ =143°20' E = +143,33°.

2. Рассчитываем РШ, РД, РМЧ:

φ2	+42,50°	λ2	+143,33°
φ1	+37,67°	λ1	-124,50°
РШ	+4,83°	РД	+267,83°
РШ	+289,8'	РД	-92,17°
		РД	-5530,2'

РМЧ = 3437,75 ln[tg(45°+42,50°/2) / tg(45°+37,67°/2)] = +379,0'.

3. Определяем значение локсодромического курса К_л:

К_л' = arccos (379,0 / = 86,0794°;

так как РД < 0, то К_л = 360° - К_л'= 273,9206°.

4. Рассчитываем S_л:

Поскольку | cos К_л | > 0,01, то S_л рассчитываем по формуле (4.4)

S_л = 289,8' / cos 273,9206° = 4238 морских миль

5. Определяем длину ортодромии D₀:

для этого приведем формулу (4.6) к рабочему виду

Cos D₀ = sin φ₁sin φ₂+ cos φ₁cos φ₂ cos РД

Подставляем заданные значения аргументов в градусах с учетом их знаков. Полученное значение D₀ переводим в минуты - морские мили.

D₀ = 67,00° = 4020' = 4020 морских миль.

6. Вычислим начальный курса плавания по ортодромии К_н:

приводим формулу (4.7) к рабочему виду

tg К_н' = sin | РД|/ (tg φ₂ cos φ₁ - sin φ₁ cos РД); приРД>0 К_н = К_н';

приРД<0 К_Н = 360°-К_Н'; К_н'=53,2°; К_н= 360° - К_н'= 306,8°

Ответ: К_л = 274°; S_л = 4238 мор. миль; Д₀ = 4020 мор. миль; К_н = 307°.

В задачах № 301 - 330 по заданным координатам точки отхода 1 ( φ₁; λ₁) и точки прихода 2 ( φ₂; λ₂) решить задачу плавания по локсодромии - рассчитать К_л и S_л. Определить длину ортодромии D₀ и начальный курс плавания по ортодромии К_н.

№	φ1		λ1		φ2		λ2
301	52°10'	N	6°35'	W	41°24'	N	73°48'	W
302	37 40	N	76 08	W	48 32	N	4 16	W
303	39 10	N	9 15	W	130	S	49 44	W
304	38 29	N	74 12	W	34 16	S	18 32	E
305	23 30	S	43 18	W	35 08	E	26 34	E
306	58 15	N	149 52	W	44 36	N	142 08	E
307	34 10	N	118 48	W	37 50	N	14120	E
308	12 35	N	87 18	W	3124	N	132 05	E
309	8 43	N	83 36	W	2 15	S	142 17	E
310	15 05	N	94 14	W	45 43	N	144 43	E
311	19 34	N	108 38	W	4 18	N	130 52	E
312	23 25	N	105 23	W	34 06	N	140 38	E
313	33 56	N	119 10	W	15 00	N	120 30	E
314	47 15	N	134 23	W	6 45	N	127 09	E
315	37 42	S	73 10	W	33 17	N	133 45	E
316	34 38	S	72 18	W	5 43	N	126 58	E
317	23 30	S	71 12	W	21 18	S	149 12	E
318	12 35	S	77 39	W	39 30	S	150 00	E
319	32 16	S	114 27	E	911	S	50 05	E
320	28 03	S	113 19	E	20 36	S	57 17	E
321	20 00	S	116 33	E	29 43	S	33 14	E
322	12 34	S	120 00	E	35 12	S	46 03	E
323	33 48	N	10 00	W	19 20	N	65 48	W
324	21 16	N	18 10	W	45 06	S	67 15	W
325	5 26	N	4 32	E	35 43	S	56 16	W
326	8 19	S	12 44	E	30 00	S	51 12	W
327	23 26	S	14 40	E	24 00	S	46 17	W
328	26 27	S	15 15	E	23 00	S	43 14	W
329	32 41	S	18 48	E	13 37	S	37 16	W
330	33 28	S	19 10	E	411	S	37 41	W