- •Практикум (лабораторный) Лабораторная работа №1.Использование простых типов данных.
- •Требования к содержанию, оформлению и порядку выполнения
- •Теоретическая часть
- •Общая постановка задачи
- •Список индивидуальных данных
- •Пример выполнения работы
- •Контрольные вопросы к защите
- •Способ оценки результатов
- •Пример выполнения работы
- •Пример выполнения работы
- •Пример выполнения работы
- •Контрольные вопросы к защите
- •Способ оценки результатов
Пример выполнения работы
Задания:
1. Вычислить
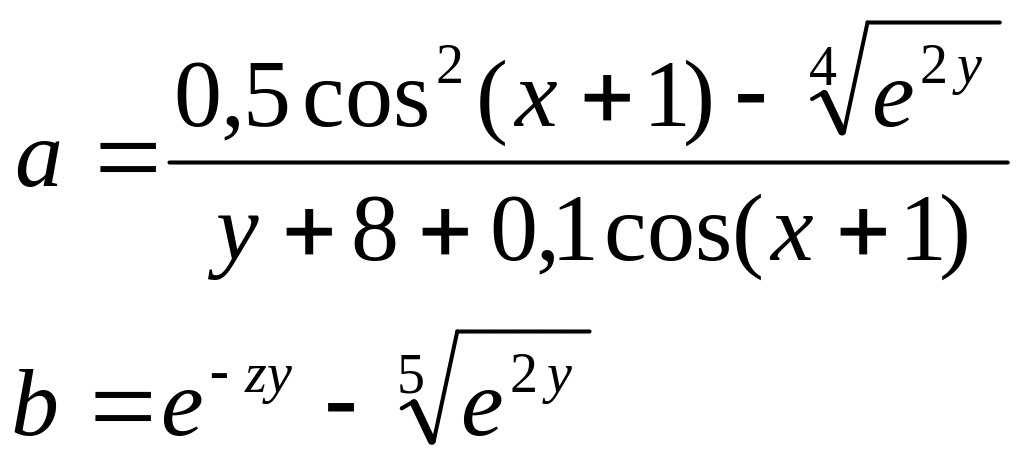
2. Верно ли, что каждое из чисел x, y, z больше нуля?
3. Вычислить:
![]() ,
,
Выполнение задания 1.
Для написания программы вычисляющей значения a и b по заданным формулам воспользуемся стандартными математическими функциями языка Си. Все заголовки математических функций перечислены в файле math.h. Базовые функции сведены в табл.Л1.2.
Все эти функции принимают double, если не определено иначе. Для работы с типами float и long double используются функции с постфиксами f и l соответственно. Все функции, принимающие или возвращающие угол, работают с радианами.
Таблица Л1.2
Имя |
Описание |
acos |
арккосинус |
asin |
арксинус |
atan |
арктангенс |
atan2 |
арктангенс с двумя параметрами |
ceil |
округление до ближайшего большего целого числа |
cos |
косинус |
cosh |
гиперболический косинус |
exp |
вычисление экспоненты |
fabs |
абсолютная величина (числа с плавающей точкой) |
floor |
округление до ближайшего меньшего целого числа |
fmod |
вычисление остатка от деления нацело для чисел с плавающей точкой |
frexp |
разбивает число с плавающей точкой на мантиссу и показатель степени. |
ldexp |
умножение числа с плавающей точкой на целую степень двух |
log |
натуральный логарифм |
log10 |
логарифм по основанию 10 |
modf(x,p) |
извлекает целую и дробную части (с учетом знака) из числа с плавающей точкой |
pow(x,y) |
результат возведения x в степень y, xy |
sin |
синус |
sinh |
гиперболический синус |
sqrt |
квадратный корень |
tan |
тангенс |
tanh |
гиперболический тангенс |
Многие из функций можно выразить через другие. При этом следует использовать следующие формулы:
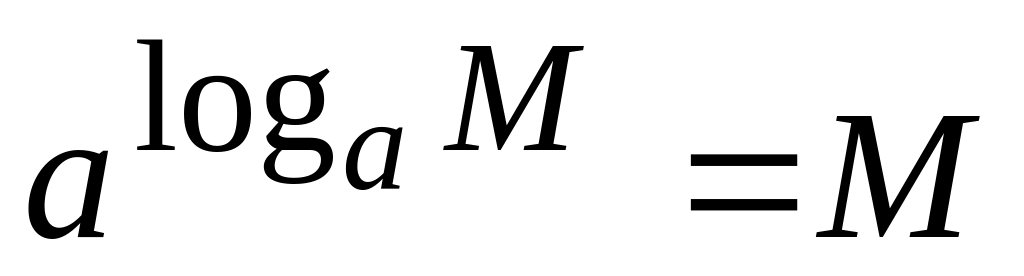 ,
пусть
,
пусть
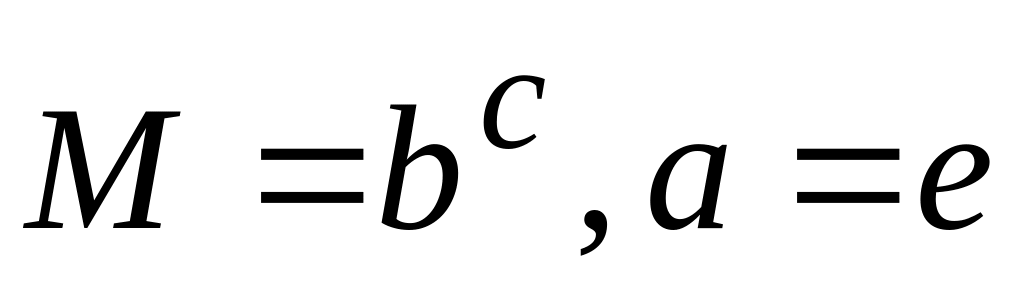 ,
тогда
,
тогда
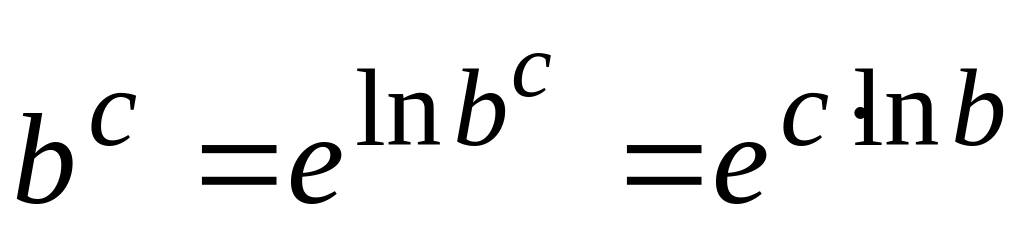
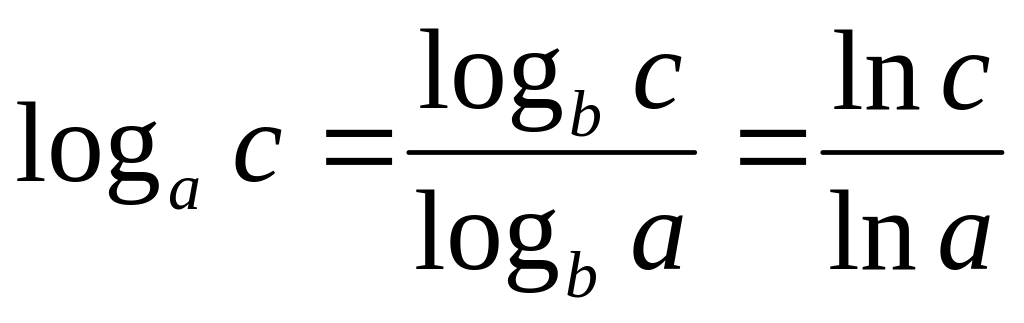
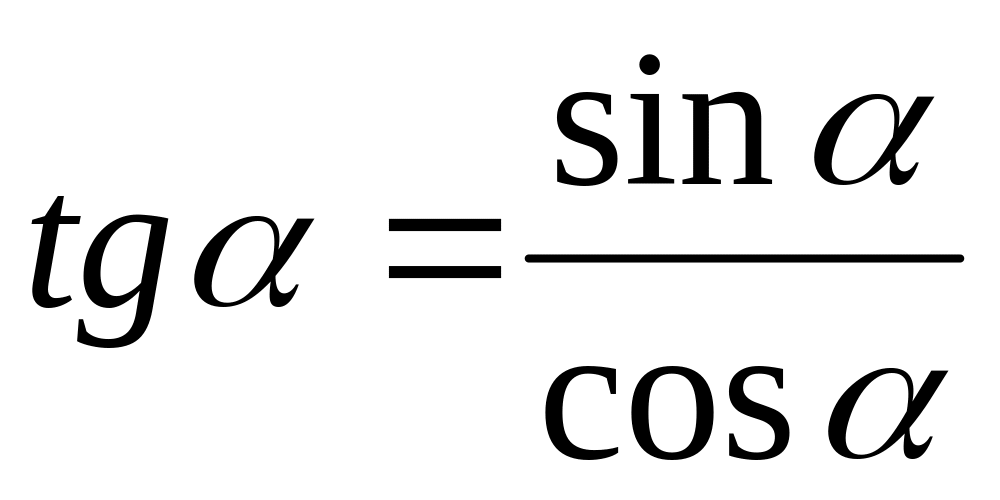
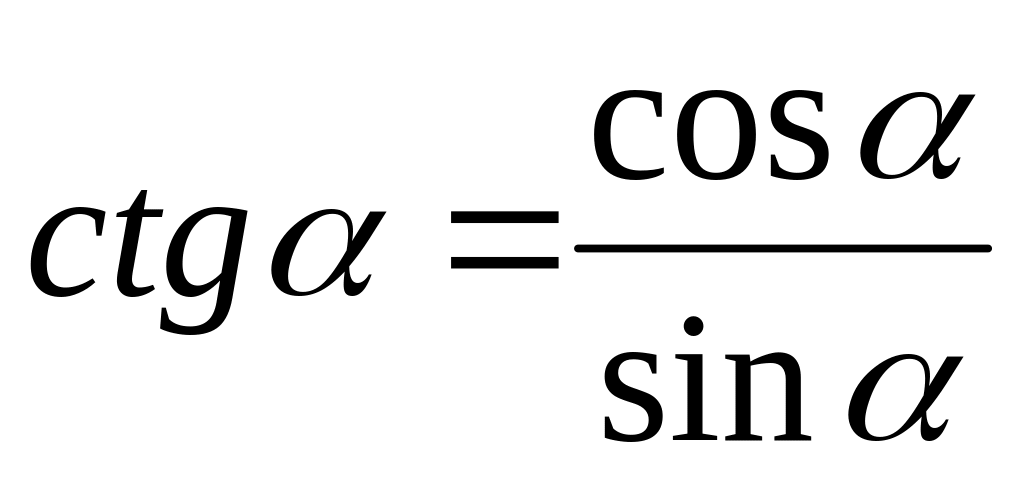
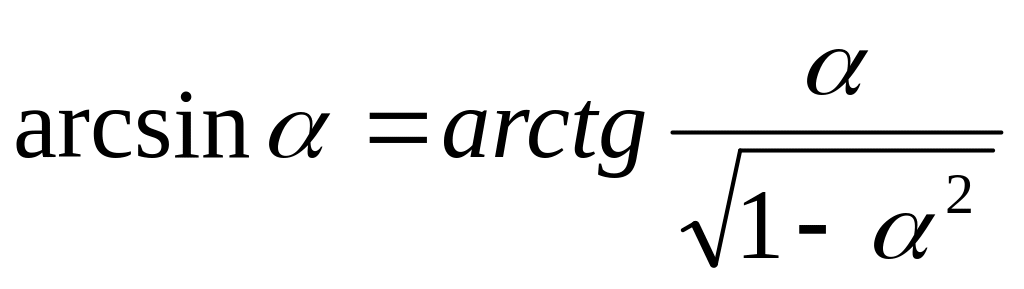
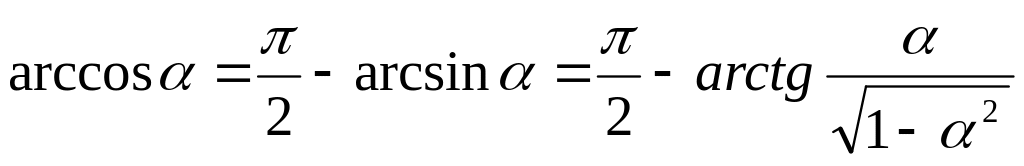
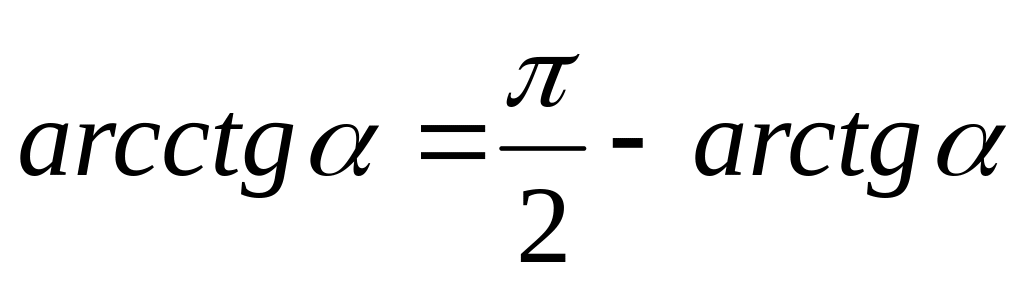 и др.
и др.
Программа для вычисления значения a и b по заданным формулам будет следующей:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
double a,b;
float x,y,z;
int main(void) {
setbuf(stdout, NULL);
printf("ЛАБОРАТОРНАЯ РАБОТА №1\n");
printf("x(рад.)="); scanf("%f",&x);
printf("y="); scanf("%f",&y);
printf("z="); scanf("%f",&z);
a=(0.5*cos(x+1)*cos(x+1)-sqrt(sqrt(exp(2*y))))/(y+8+0.1*cos(x+1));
printf("a=%f\n",a);
b=exp(-z*y)-pow(exp(2*y),1.0/5.0);
printf("b=%f\n",b);
printf("Работа программы завершена.\n");
return EXIT_SUCCESS;
}
Создадим проект "Лаб.раб.1" (см.рис.Л1.3, Л1.10).
Ведем текст программы. Обратите внимание на команду setbuf(stdout, NULL). Данная команда нужна для перевода консоли в общепринятый режим работы.
Выполним компиляцию (рис.Л1.8) и запустим программу на выполнение. Результат представлен на рис. Л1.11.
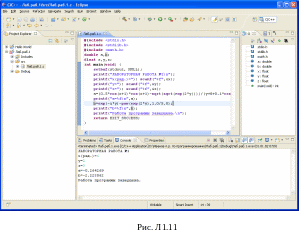
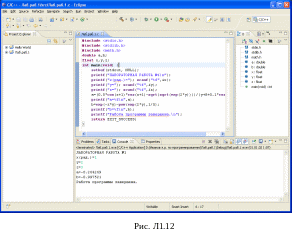
Обратите внимание на запись pow(exp(2*y),1.0/5.0) в тексте программы. Здесь для извлечения корня пятой степени (возведение в степень 1/5) используется запись 1.0/5.0. Если использовать запись 1/5, то результат будет неверным (Рис.Л1.12). Это связано с тем, что запись 1/5 определяет целочисленное деление 1 на 5.
Подбор тестовых данных выполните самостоятельно.
Выполнение задания 2.
Для определения факта, что каждое из заданных чисел x, y, z больше нуля можно предложить несколько алгоритмов. Три из таких алгоритмов представлены блок-схемами на рис.Л1.13-Л1.15.
Алгоритм 1 (рис.Л1.13) в условных блоках содержать только одну операцию отношения. Алгоритм 2 (рис.Л1.14) имеет один условный блок, в котором записано логическое выражение, состоящее из операций отношения и логических операций. Алгоритмы 1 и 2 не используются рабочие переменные. В алгоритме 3 (рис.Л1.15) используется целочисленная рабочая переменная в качестве счётчика.
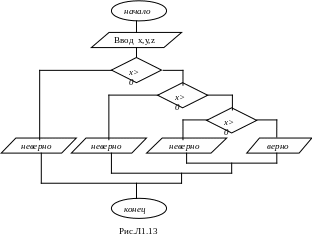
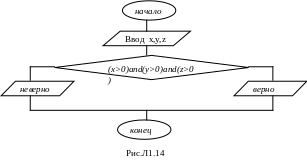
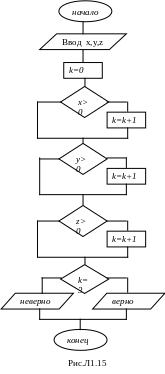
Достаточно реализовать один из вариантов алгоритма. Программа, реализующая второй вариант алгоритма (рис.Л1.14) будет следующей:
#include <stdio.h>
#include <stdlib.h>
float x,y,z;
int main(void) {
setbuf(stdout, NULL);
printf("ЛАБОРАТОРНАЯ РАБОТА №1 (задание 2)\n");
printf("x="); scanf("%f",&x);
printf("y="); scanf("%f",&y);
printf("z="); scanf("%f",&z);
if((x>0)&&(y>0)&&(z>0)) printf("Верно\n");
else printf("Неверно\n");
printf("Работа программы завершена.\n");
return EXIT_SUCCESS;
}
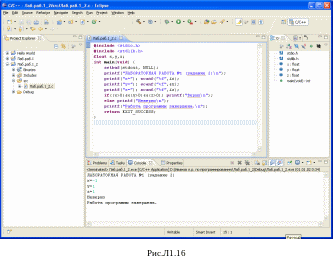
Тестовые данные представлены в табл.Л1.3. Результат работы программы представлен на рис.Л1.16.
Таблица Л1.3
Номер набора |
Исходные данные |
Результат |
||
x |
y |
z |
||
1 |
-1 |
-1 |
-1 |
неверно |
2 |
-1 |
-1 |
1 |
неверно |
3 |
-1 |
1 |
-1 |
неверно |
4 |
-1 |
1 |
1 |
неверно |
5 |
1 |
-1 |
-1 |
неверно |
6 |
1 |
-1 |
1 |
неверно |
7 |
1 |
1 |
-1 |
неверно |
8 |
1 |
1 |
1 |
верно |
Выполнение задания 3.
Даны числа x и E (E>0). Вычислить приближенное значение суммы
,
где
![]() .
Нужное приближение получено, если
очередное слагаемое меньше E.
.
Нужное приближение получено, если
очередное слагаемое меньше E.
Алгоритм нахождения требуемой суммы представлен блок-схемой на рис. Л.1.4.
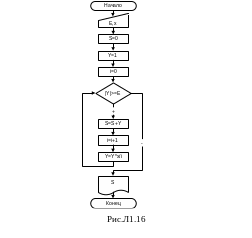
Рассмотрим один
из тестов. Пусть x=2 и E=0.5,
тогда будет получен следующий результат
![]() ,
т.к.
,
т.к.![]() ,
а
,
а
![]() .
Результат работы данной программе на
рассмотренных тестовых данных представлен
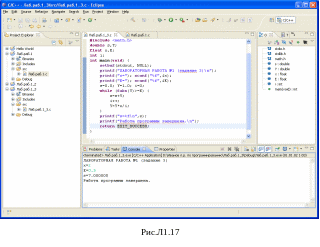
на рис.Л1.17.
.
Результат работы данной программе на
рассмотренных тестовых данных представлен
на рис.Л1.17.