Оценка погрешностей измерений при выполнении лабораторных работ по физике

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой полученных результатов. Поскольку не существует абсолютно точных приборов и других средств измерения, следовательно, не бывает и абсолютно точных результатов измерения. Погрешности возникают при любых измерениях, и только правильная оценка погрешностей проведенных измерений и расчетов позволяет выяснить степень достоверности полученных результатов.

Абсолютная погрешность измерения

Рисунок 1

Предположим, что диаметр стержня, измеренный штангенциркулем, оказался равным 14 мм. Можно ли быть уверенным, что он пройдет в “идеальное” отверстие того же диаметра? Если бы этот вопрос был поставлен чисто ”теоретически“, то ответ был бы утвердительным, но на практике может получиться иначе. Диаметр стержня был определен с помощью реального измерительного прибора, следовательно, с некоторой погрешностью. Значит 14 мм - это приближенное значение диаметра – X_пр. Определить его истинное значение невозможно, можно только указать некоторые границы достоверности полученного приближенного результата, внутри которых находится истинное значение диаметра нашего стержня. Эта граница называется границей абсолютной погрешности и обозначается ΔX (её часто называют просто абсолютной погрешностью). Поэтому наш стержень может пройти в отверстие, а так же может и не пройти в него: все зависит от того, в каком месте интервала [X_{пр -} ΔX, X_{пр +} ΔX] находится истинное значение диаметра нашего стержня. На рисунке 1 показан случай, когда стержень в отверстие не пройдет.

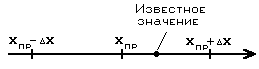
Итак, абсолютная погрешность показывает, насколько неизвестное экспериментатору истинное значение измеряемой величины может отличаться от измеренного значения.

Результат измерения с учетом абсолютной погрешности записывают так:

Относительная погрешность измерения

Значение абсолютной погрешности все же не позволяет в полной мере оценить качество наших измерений. Если, например, в результате измерений установлено, что длина стола с учетом абсолютной погрешности равна (100± 1) см, а толщина его крышки равна (2 ± 1) см, то качество измерений в первом случае выше (хотя граница абсолютной погрешности измерений в обоих случаях одинакова). Качество измерений характеризуется относительной погрешностью ε, равной отношению абсолютной погрешности ΔX к значению величины X_пр, получаемой в результате измерения:

.

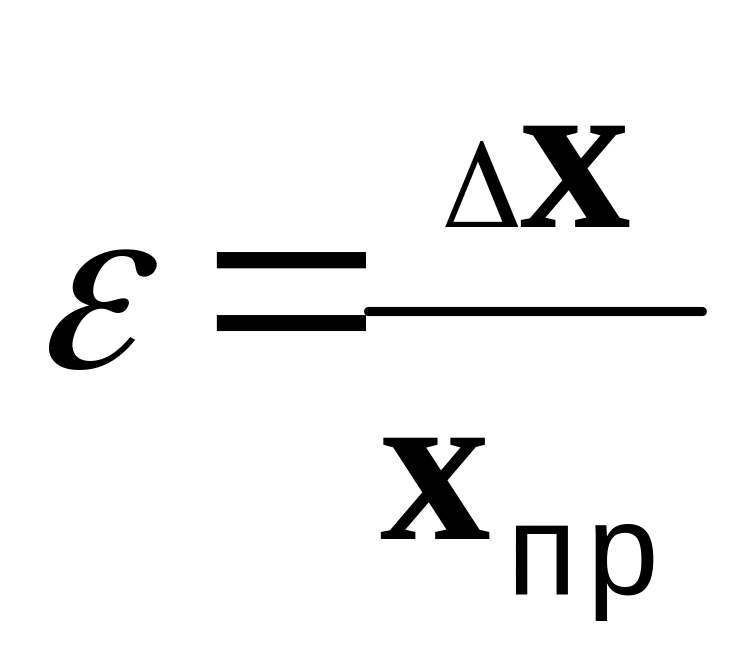При выполнении лабораторных работ выделяют следующие виды погрешностей: погрешности прямых измерений; погрешности косвенных измерений; случайные погрешности и систематические погрешности.

Погрешности прямых измерений

Прямое измерение - это такое измерение, при котором его результат определяется непосредственно в процессе считывания со шкалы прибора. В нашем первом примере с определением диаметра стержня речь шла как раз о таком измерении. Погрешность прямого измерения обозначается значком Δ. Если вы умеете правильно пользоваться измерительным прибором, то погрешность прямого измерения зависит только от его качества и равна сумме инструментальной погрешности прибора (Δ _и) и погрешности отсчета (Δ ₉). Таким образом: Δ = Δ _и + Δ _о

Инструментальная погрешность измерительного прибора (Δ_и) определяется на заводе-изготовителе. Абсолютные инструментальные погрешности измерительных приборов, чаще всего используемых для проведения лабораторных работ, приведены в таблице 1.

Таблица 1

Средства измерения	Предел измерения	Цена деления	Инструментальная погрешность
Линейка ученическая	До 30 см	1 мм	1 мм
Линейка чертежная	До 50 см	1 мм	0,2 мм
Линейка инструментальная (стальная)	До 30 см	1 мм	0,1 мм
Линейка демонстрационная	100 см	1 см	0,5 см
Лента измерительная	150 см	0,5 см	0,25 см
Измерительный цилиндр	до 250 мл	1 мл	1 мл
Штангенциркуль	150 мм	0,1 мм	0,05 мм
Микрометр	25 мм	0,01 мм	0,005 мм
Динамометр учебный	4 Н	0,1 Н	0,05 Н
Секундомер электронный	100 с	0,01 с	0,01 с
Барометр-анероид	720-780 мм.рт.ст	1 мм.рт.ст.	3 мм.рт.ст.
Термометр спиртовой	0-100оС	1оС	1оС
Термометр ртутный	До 250оС	1оС	0,5оС
Амперметр школьный	2 А	0,1 А	0,05 А
Вольтметр школьный	6 В	0,2 В	0,15 В

Погрешность отсчета измерительного прибора (Δ _о) связана с тем, что указатель прибора не всегда точно совпадает с делениями шкалы. В этом случае погрешность отсчета не превосходит половины цены деления шкалы.

Поэтому абсолютную погрешность прямого измерения находят по формуле ., где с - цена деления шкалы измерительного прибора.

Учитывать погрешность отсчета надо только в тех случаях, когда указатель прибора при измерении находится между нанесенными на шкалу прибора делениями. Не имеет смысла учитывать, погрешности отсчета у цифровых измерительных приборов.

Одновременно учитывать обе составляющие погрешности прямого измерения следует лишь в том случае, если их значения близки друг к другу. Любым из этих слагаемых можно пренебречь, если оно не превосходит одной трети или одной четверти второго. В этом состоит так называемое правило "ничтожных погрешностей".