17.4 Метод получения топологических уравнений

Эквивалентная схема технической системы может быть представлена в виде графа, ребра которого изображают двухполюсники, замещающие элементы (компоненты) системы. Пусть задан граф (рис. 11) некоторой технической системы. Топологические уравнения равновесия (типа уравнений первого закона Кирхгофа) могут быть записаны для каждого сечения, которое может включать один или несколько узлов. Для узлов, отмеченных на рис. 11, можем записать (принимая знак минус при направлении ребер к рассматриваемому узлу) следующие уравнения:

сечение 1 ;

сечение 1-5 ;

сечение 2 (11)

сечение 4 .

Топологические уравнения неразрывности (аналоги второго закона Кирхгофа) будут иметь вид:

(12)

Процедура получения уравнений (11), (12) может быть формализована. Для этой цели вводят матрицу контуров и сечений – М-матрицу. Такую матрицу строят с помощью ориентированного графа эквивалентной схемы и выбранного для этого графа дерева. Количество столбцов матрицы соответствует числу ветвей дерева, а количество строк – числу хорд.

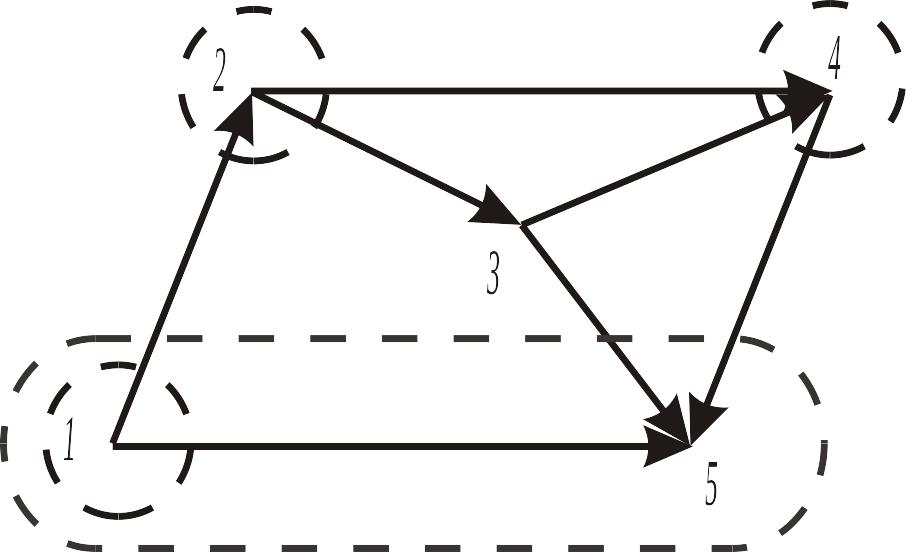
Рис.11. Граф эквивалентной схемы

При формировании М-матрицы хорды поочередно включают в дерево с образованием замкнутого контура. При обходе этого контура в направлении включенной хорды формируют строку матрицы. В столбцах матрицы, соответствующих ветвям дерева, ставят +1 при совпадении направления ветви с направлением обхода и -1, если направления противоположны.

Рассмотрим построение М-матрицы (табл. 1) для графа, показанного на рис. 11. Принимая пятый узел за базовый, построим дерево графа (рис. 12). При подключении хорды 1-2 образуется контур 1-2, 2-3, 3-5, 1-5,поэтому в первой строке матрицы будем иметь ‒ 1 (для ветви 1-5), + 1 (для ветвей 2-3, 3-5) и 0 (для ветви 3-4). Аналогично заполняют остальные строки.

Таблица 10.2

Хорды	Ветви дерева
	1 – 5	3 – 5	2 – 3	3 – 4
1 – 2 2 – 4 4 – 5	-1 0 0	1 0 -1	1 -1 0	0 -1 1

Топологические уравнения с использованием М-матрицы имеют вид:

(13)

где – векторы переменных типа разности потенциалов на ветвях дерева и хордах;

– векторы переменных типа потока для ветвей дерева и хорд.

Записывая первое уравнение (13) в развернутом виде

вы можете убедиться, что оно совпадает с системой уравнений (12). Аналогично, второе уравнение (13) совпадает с (11). Таким образом, использование М-матрицы позволяет формализовать процедуру получения математической модели. При этом сечения дерева специально выбирать не надо. Выше такие сечения приведены для наглядности.

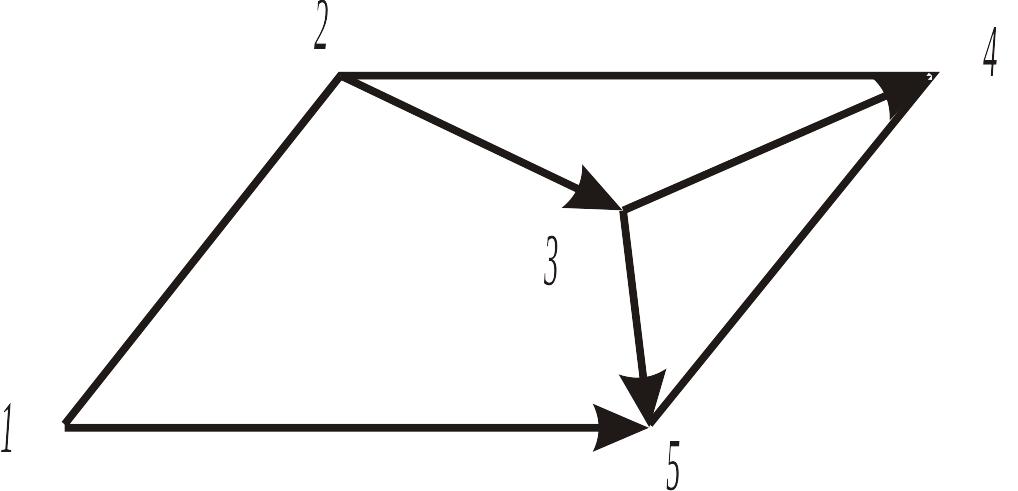
Рис.12. К построению М-матрицы

Возможна иная формализация процедуры построения математической модели с использованием матрицы инциденций. Будем рассматривать исходный граф (см. рис, 11) как хорды некоторого фиктивного дерева (рис. 13), ветви которого на рисунке изображены пунктирными линиями.

Составим М-матрицу, поочередно включая в фиктивное дерево хорды исходного графа. Так, контур 1-5 состоит из хорды 1-5 и ветви 1-5, направление которой противоположно хорде, поэтому в М-матрице этой ветви будет отвечать значение – 1. В контуре 2-3-5 направление ветви 3-5 совпадает с направлением хорды, а для ветви 2-5 – не совпадает, поэтому будем соответственно иметь +1 и -1. Включая последовательно все хорды, получим М-матрицу (рис. 13), приведенную в табл. 2, или, выделяя содержательную часть М-матрицы.

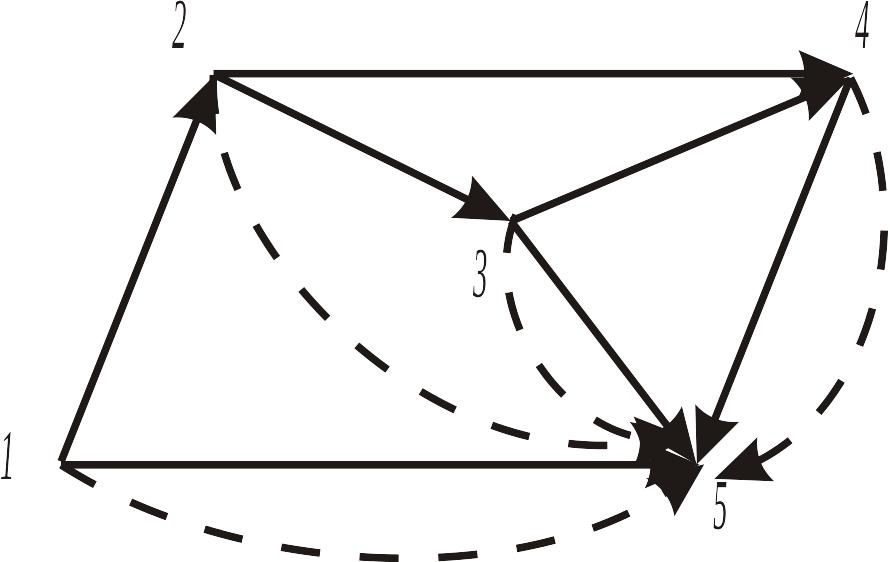
Рис.13. Граф с фиктивным деревом

(14)

Таблица 10.3

Хорды	Ветви дерева
	1 – 5	2 – 5	3 – 5	4 – 5
1 – 5 3 – 5 4 – 5 3 – 4 1 – 2 2 – 4 2 – 3	-1 0 0 0 -1 0 0	0 0 0 0 1 -1 -1	0 -1 0 -1 0 0 1	0 0 -1 1 0 1 0

Рассмотрим второе уравнение системы (13), которое будет справедливо для М-матрицы (14), но с некоторым отличием. Это отличие связано с тем, что было построено фиктивное дерево, поэтому в ветвях его не будет токов и, следовательно, исходное уравнение примет вид . Индекс «х» у вектора J мы опустили, поскольку хордами являются все ребра исходного графа. Обратите внимание, что транспонированная М-матрица представляет собой не что иное, как матрицу инциденций исходного графа (см. рис.), записанную с обратными знаками:

(15)

Все это позволяет записать второе уравнение системы (13) в ином виде: .

Первое уравнение системы (13) изменится следующим образом. Разность потенциалов ветвей дерева Uvd есть разность потенциалов i-й и базовой точек, т. е. потенциал i-й точки . М-матрица будет равна , поэтому первое уравнение системы (13) примет вид .

Все сказанное дает возможность записать систему уравнений (13) в следующей форме:

(16)

Таким образом, возможны два способа формализации процедур построения математической модели для описания эквивалентной схемы технического объекта, в одном из которых используют систему уравнений (13) и М-матрицу, в другом – систему уравнений (16) и матрицу инциденций ориентированного графа.

В качестве примера рассмотрим механическую систему (рис. 14, а), эквивалентная схема (б) и граф (в) которой изображены на рисунке. Матрица инциденций приведена в табл. 3.

Таблица 3

Узлы графа	Дуги графа
	F	R1	L1	L2	R2	R3	m1	m2	m3
1 2 3	-1	1	1 -1	1 -1	1	1	1	1	1

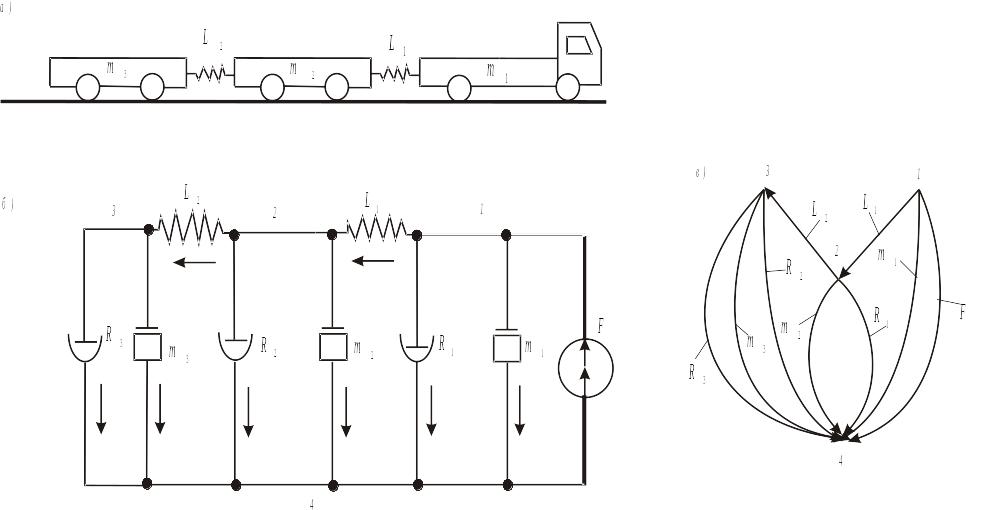
Рис. 14. К примеру механической системы

Первое уравнение (16) в развернутой форме имеет вид:

где потоковые переменные JR, JL, Jm=Jc типов R, L, С можно записать в форме приведенных выше зависимостей между фазовыми переменными. В результате будет получена система дифференциальных уравнений. Транспонируя матрицу инциденций и используя второе уравнение системы (16), аналогично можно получить систему дифференциальных уравнений для переменных типа потенциала.

Литература:

1. Ильина Н.В. Системный анализ и моделирование процессов в техносфере: Учеб. пособие / Н.В. Ильина, Д.Д. Лапшин, В.И. Федянин. – Ч. 1. Воронеж: ГОУВПО «Воронежский государственный технический университет, 2008. – 206 с.

Лекция 18. Многокритериальная оптимизация