
- •Системный анализ и моделирование процессов в техносфере
- •1.1. Понятие системы. Базовые категории систем
- •1.2. Классификация систем
- •1.3. Общее представление о системном анализе
- •1.4. Принципы системного анализа
- •2.1. Этапы анализа и синтеза
- •2.2. Понятие о структурном анализе
- •2.3. Методы декомпозиции
- •2.4. Требования, предъявляемые к декомпозиции
- •2.5. Алгоритм декомпозиции
- •2.5. Программно-целевой подход к решению системных задач
- •1. Область применения и этапы программно-целевого подхода
- •2. Дерево целей
- •3.1. Агрегирование системы и эмерджентность
- •3.2. Виды связей в системе
- •Связи взаимодействия (координации):
- •Связи преобразования:
- •3.3. Виды агрегирования
- •4.1. Общие свойства процесса принятия решений
- •4.2. Участники процесса принятия решения
- •4.3. Схема ппр
- •4.4. Формулирование проблемы
- •4.5. Определение целей
- •4.6. Генерирование альтернатив
- •4.7. Формирование критериев
- •4.8. Физиология принятия решений
- •4.9. Виды и особенности задач принятия решений
- •4.10. Формализация принятия решений
- •Лекция 5. Информационное обеспечение ппр
- •5.1. Понятие информации
- •5.2. Информационная структура процесса принятия решений
- •6.1. Особенности группового выбора
- •6.2. Экспертные методы выбора
- •6.3. Методы типа мозговой атаки или коллективной генерации идей
- •6.4. Методы типа сценариев
- •6.5. Методы типа «Делфи»
- •6.6. Методы типа дерева целей
- •6.7. Морфологические методы
- •7.1 Основные положения теории управления
- •7.2 Аксиомы теории управления
- •7.3 Модели основных функций организационно-технического управления
- •7.4 Описание функций управления
- •Лекция 8. Понятие и классификация моделей
- •8.1 Понятие модели, моделирования
- •8.2 Познавательные и прагматические модели
- •8.3 Статические и динамические модели
- •8.4 Классификация моделей по способу воплощения
- •8.5 Место математического моделирования в системных исследованиях
- •8.6 Типы и виды математических моделей
- •8.7 Процесс построения математической модели
- •8.8 Структура моделирования происшествий в техносфере
- •9.1 Конфликт ‒ предмет рассмотрения теории игр
- •9.2 Понятие игры. Классификация игр. Формальное представление игр
- •9.3 Определение бескоалиционной игры
- •9.4 Приемлемые ситуации и ситуации равновесия
- •9.5 Примеры игровых задач
- •10.1 Граф и его виды
- •10.2 Задача о кратчайшем пути
- •10.3 Задача о максимальном потоке
- •11.1 Поверхность отклика
- •11.2 Этапы планирования эксперимента
- •11.3 Обработка и анализ результатов моделирования
- •12.1 Полный факторный эксперимент
- •12.2 Дробный факторный эксперимент
- •12.3 Метод наименьших квадратов
- •13.1 Основная цель кластерного анализа
- •13.2 Объединение (древовидная кластеризация)
- •13.3 Двувходовое объединение
- •13.4 Метод k средних
- •13.5 Алгоритм нечеткой кластеризации
- •14.1 Понятие когнитивного моделирования
- •14.2 Подсистема представления субъективной информации
- •14.3 Подсистема извлечения предпочтений эксперта
- •14.4 Подсистема обработки
- •14.5 Подсистема представления результатов моделирования
- •14.6 Подсистема поддержки аналитической деятельности эксперта
- •14.7 Моделирование бизнес процессов на основе bpmn-диаграмм
- •14.8 Метод анализа иерархий (маи): введение
- •14.9 Основные принципы маи
- •1. Принцип идентичности и декомпозиции
- •2. Принцип дискриминации и сравнительных суждений
- •3. Принцип синтеза
- •14.10 Общая оценка маи как метода принятия решений
- •15.1 Общий ход решения задачи на основе метода конечных элементов
- •15.2 Сети одномерных конечных элементов
- •15.3 Виды конечных элементов
- •16.1 Основные понятия
- •16.2 Приближенное решение оду при заданных начальных условиях
- •16.3 Метод Эйлера и его модификации
- •16.4 Метод Рунге-Кутта
- •16.5 Приближенное решение ду n-го порядка при заданных начальных условиях
- •16.6 Приближенное решение ду при заданных граничных условиях (краевых задач)
- •16.6.1 Метод начальных параметров
- •16.6.2 Редукция к задаче Коши для линейного ду второго порядка
- •17.1 Основные понятия
- •17.2 Типы элементов
- •17.3 Источники энергии и преобразователи. Аналоги топологических уравнений
- •17.4 Метод получения топологических уравнений
- •18.1 Свойства задач принятия решения со многими критериями
- •18.2. Формирование множества критериев
- •18.3 Методология решения многокритериальных задач
- •18.4 Технологии отыскания эффективных решений
- •18.5 Методы принятия решения при нескольких критериях
15.3 Виды конечных элементов
Выше
были рассмотрены системы, включающие
одномерные симплекс-элементы, при этом
функции формы элемента (4) оставались
одинаковыми для задач из разных предметных
областей. Физическая сущность задачи
отображается матрицей жесткости. В
электрических системах эта матрица
зависит от сопротивлении R,
емкостей С,
индуктивностей L
элементов,
составляющих систему. В системах,
характеризующих работу строительных
конструкций, матрица жесткости
непосредственно связана с погонными
жесткостями
для растянутых (сжатых) элементов,
![]() – для изгибаемых элементов и т.д. Для
нелинейных систем, например, для схемы
«в» (рис. 2), где связь между напором V
и расходом
J
имеет вид
– для изгибаемых элементов и т.д. Для
нелинейных систем, например, для схемы
«в» (рис. 2), где связь между напором V
и расходом
J
имеет вид
![]() ,
матрица
жесткости будет представлять уже не
массивы констант, а некоторые функции
от напора жидкости.
,
матрица
жесткости будет представлять уже не
массивы констант, а некоторые функции
от напора жидкости.
В случае функции двух переменных х, у используют плоские конечные элементы в виде многоугольников, обычно треугольника и прямоугольника.
Рассмотрим двумерный симплекс-элемент, представляющий собой плоский треугольник (рис. 4).
Интерполяционный полином, аппроксимирующий непрерывную функцию v(x, у) внутри симплекс-элемента, имеет вид
![]() (16)
(16)
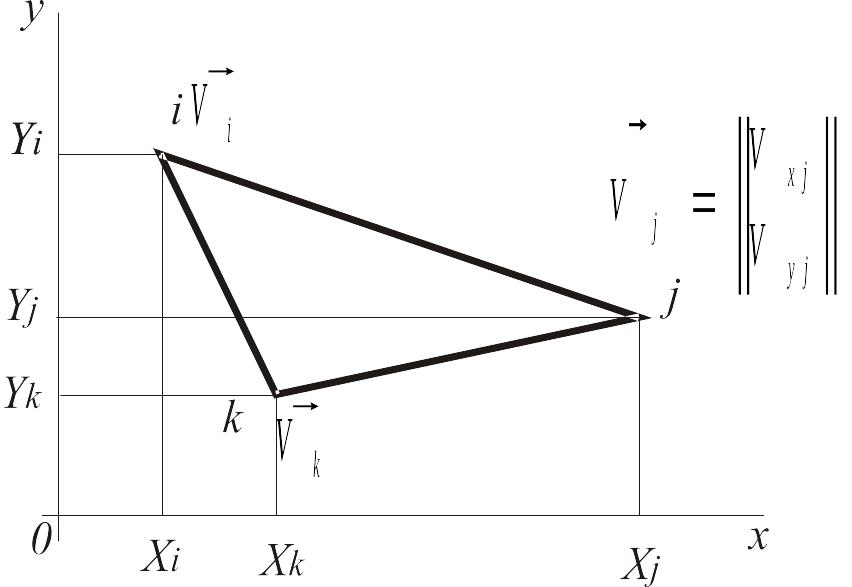
Рис. 4. Двумерный симплекс-элемент
Для придания этому выражению вида, удобного для применения в методе конечных элементов, будем поступать так же, как это делали на втором этапе п.п. 15.1 [см. формулы (1)...(6)]. Граничные условия будут иметь вид:
при
![]() функция v(x,
у) примет
значение
функция v(x,
у) примет
значение![]() ;
;
при
![]() функция
v(x,
у) примет
значение
функция
v(x,
у) примет
значение![]() .
.
Используя
формулу (16), получим систему трех уравнений
для определения коэффициентов
![]() Подставляя эти коэффициенты в полином
(16) и проделав необходимые преобразования,
аналогичные рассмотренным в п. 15.1,
запишем аналогичную (5) формулу
Подставляя эти коэффициенты в полином
(16) и проделав необходимые преобразования,
аналогичные рассмотренным в п. 15.1,
запишем аналогичную (5) формулу
![]() (17)
(17)
где функции формы элемента имеют вид:
 (18)
(18)
Здесь ∆ – площадь треугольника конечного элемента;
![]() – коэффициенты,
определяемые путем круговой перестановки
индексов выражений:
– коэффициенты,
определяемые путем круговой перестановки
индексов выражений:
![]() . (19)
. (19)
Формулы
(16)...(19) будут одинаковыми для всех задач,
где используют треугольные симплекс-элементы.
Матрицы жесткостей будут зависеть от
физической сущности задачи. Рассмотрим
это на примере плоской задачи теории
упругости. Заметим, что в этом случае
каждый узел имеет две степени свободы,
поэтому вектор
имеет
две компоненты vx
и
![]() каждую
из которых определяют по формуле (17).
каждую
из которых определяют по формуле (17).
Деформации внутри конечного элемента можно выразить через перемещения с помощью зависимостей Коши:
![]()
Выполняя дифференцирование равенства (17) с учетом обозначений (18), запишем зависимости Коши в матричной форме:
 (20)
(20)
или
![]() . (20
а)
. (20
а)
Для перехода от деформаций тела к напряжениям используем закон Гука при плоском напряженном состоянии:
 (21)
(21)
или
![]() . (21
а)
. (21
а)
Матрицы
D
и В
содержат всю информацию о конечном
элементе: матрица D
определяет его упругие характеристики
а матрица В
– геометрические. Остается определить
еще одну матрицу (матрицу жесткости К),
которая связывает усилия, действующие
в узлах конечного элемента, с перемещениями
этих узлов. Для записи этой матрицы
воспользуемся принципом возможных
перемещений, согласно которому при
равновесии тела работа внешних сил Р
на возможных
перемещениях узлов
![]() т.
е.
т.
е.
![]() равна
по величине работе внутренних сил на
тех же перемещениях:
равна
по величине работе внутренних сил на
тех же перемещениях:
![]() ,
где
,
где
![]() –
деформация, отвечающая возможным
перемещениям;
–
деформация, отвечающая возможным
перемещениям;
![]() – объем конечного элемента. В результате
преобразований получим искомую связь
между усилиями в узлах конечного элемента
и перемещениями этих узлов:
– объем конечного элемента. В результате
преобразований получим искомую связь
между усилиями в узлах конечного элемента
и перемещениями этих узлов:
![]() , (22)
, (22)
где матрица жесткости К будет равна
![]() (23)
(23)
Матрица жесткости (23) конечного элемента не зависит от действующих на элемент нагрузок и поэтому остается неизменной для всех нагружений. Элементы этой матрицы представляют собой коэффициенты канонических уравнений метода перемещений для расчета одного конечного элемента.
Рассмотрим объединение конечных элементов в ансамбль на примере простейшей сети из трех конечных элементов (рис. 5).
Для
каждого конечного элемента мы можем
записать формулу (17), заменяя узлы
![]() конкретными номерами. Так, для первого
элемента
конкретными номерами. Так, для первого
элемента
![]() .
.
Поступая аналогично с остальными узлами, получим:
 (24)
(24)
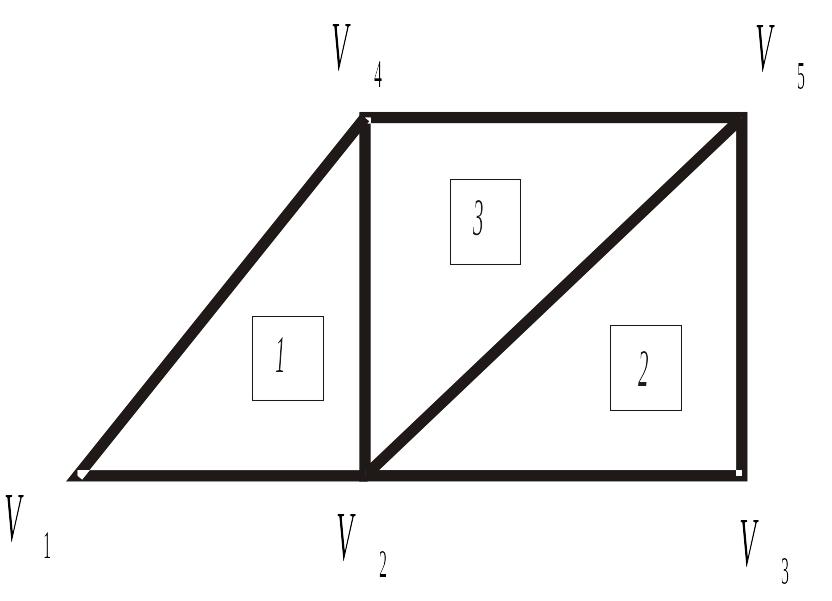
Рис.5. Ансамбль трех конечных элементов
Напомним, что узловые значения искомой функции
![]()
пока еще не известны и подлежат определению. С этой целью нужно использовать какой-нибудь принцип, выражающий физическую сущность задачи. В задачах строительной механики таким принципом могут быть уравнения равновесия с учетом совместности перемещений. Когда мы все это проделаем, задача будет решенной, поскольку формулы (20), (21), (24) с учетом обозначений (18), (19) позволяют определить в любой точке области нормальные и касательные напряжения, найти угловые и линейные деформации, вычислить перемещения данной точки в направлении осей х и у. Совокупность указанных формул, полностью определяющих поведение исследуемой системы, составляет ее математическую модель.
Перейдем к объединению конечных элементов в ансамбль.
Пусть в узлах системы конечных элементов действуют внешние силы, определяемые вектором
![]() (25)
(25)
К
каждому i-му
узлу сети примыкает в общем случае
![]() конечных элементов, каждый из которых
вносит свой вклад в матрицу жесткости.
Поэтому для каждого i-го
узла суммарная матрица жесткости будет
представлять собой сумму элементов
матриц жесткости всех примыкающих к
узлу элементов, т.е.
конечных элементов, каждый из которых
вносит свой вклад в матрицу жесткости.
Поэтому для каждого i-го
узла суммарная матрица жесткости будет
представлять собой сумму элементов
матриц жесткости всех примыкающих к
узлу элементов, т.е.
![]() , (26)
, (26)
в
то время, как узловые перемещения для
всех этих элементов будут общими в силу
совместности перемещений всех элементов,
соединенных в i-м
узле. Поскольку узлы имеют две степени
свободы, вектор перемещения i-го
узла будет содержать две компоненты
перемещений
![]() точно
так же, как внешняя сила [см. формулу
(25)] имеет две компоненты Pxi,
Pyi.
Совокупность
перемещений всех m
неопорных
узлов сети конечных элементов определится
m-мерным
вектором перемещений:
точно
так же, как внешняя сила [см. формулу
(25)] имеет две компоненты Pxi,
Pyi.
Совокупность
перемещений всех m
неопорных
узлов сети конечных элементов определится
m-мерным
вектором перемещений:
![]() (27)
(27)
Общую матрицу жесткости для всей конструкции можно выразить в виде
![]() . (28)
. (28)
Окончательная зависимость между вектором сил (25) и вектором перемещений (27) будет иметь вид
. (29)
Таким образом, вектор узловых значений искомой функции будет равен
![]() . (30)
. (30)
Литература:
1. Ильина Н.В. Системный анализ и моделирование процессов в техносфере: Учеб. пособие / Н.В. Ильина, Д.Д. Лапшин, В.И. Федянин. – Ч. 1. Воронеж: ГОУВПО «Воронежский государственный технический университет, 2008. – 206 с.
Лекция 16. Аналитические модели сложных систем
