
- •Системный анализ и моделирование процессов в техносфере
- •1.1. Понятие системы. Базовые категории систем
- •1.2. Классификация систем
- •1.3. Общее представление о системном анализе
- •1.4. Принципы системного анализа
- •2.1. Этапы анализа и синтеза
- •2.2. Понятие о структурном анализе
- •2.3. Методы декомпозиции
- •2.4. Требования, предъявляемые к декомпозиции
- •2.5. Алгоритм декомпозиции
- •2.5. Программно-целевой подход к решению системных задач
- •1. Область применения и этапы программно-целевого подхода
- •2. Дерево целей
- •3.1. Агрегирование системы и эмерджентность
- •3.2. Виды связей в системе
- •Связи взаимодействия (координации):
- •Связи преобразования:
- •3.3. Виды агрегирования
- •4.1. Общие свойства процесса принятия решений
- •4.2. Участники процесса принятия решения
- •4.3. Схема ппр
- •4.4. Формулирование проблемы
- •4.5. Определение целей
- •4.6. Генерирование альтернатив
- •4.7. Формирование критериев
- •4.8. Физиология принятия решений
- •4.9. Виды и особенности задач принятия решений
- •4.10. Формализация принятия решений
- •Лекция 5. Информационное обеспечение ппр
- •5.1. Понятие информации
- •5.2. Информационная структура процесса принятия решений
- •6.1. Особенности группового выбора
- •6.2. Экспертные методы выбора
- •6.3. Методы типа мозговой атаки или коллективной генерации идей
- •6.4. Методы типа сценариев
- •6.5. Методы типа «Делфи»
- •6.6. Методы типа дерева целей
- •6.7. Морфологические методы
- •7.1 Основные положения теории управления
- •7.2 Аксиомы теории управления
- •7.3 Модели основных функций организационно-технического управления
- •7.4 Описание функций управления
- •Лекция 8. Понятие и классификация моделей
- •8.1 Понятие модели, моделирования
- •8.2 Познавательные и прагматические модели
- •8.3 Статические и динамические модели
- •8.4 Классификация моделей по способу воплощения
- •8.5 Место математического моделирования в системных исследованиях
- •8.6 Типы и виды математических моделей
- •8.7 Процесс построения математической модели
- •8.8 Структура моделирования происшествий в техносфере
- •9.1 Конфликт ‒ предмет рассмотрения теории игр
- •9.2 Понятие игры. Классификация игр. Формальное представление игр
- •9.3 Определение бескоалиционной игры
- •9.4 Приемлемые ситуации и ситуации равновесия
- •9.5 Примеры игровых задач
- •10.1 Граф и его виды
- •10.2 Задача о кратчайшем пути
- •10.3 Задача о максимальном потоке
- •11.1 Поверхность отклика
- •11.2 Этапы планирования эксперимента
- •11.3 Обработка и анализ результатов моделирования
- •12.1 Полный факторный эксперимент
- •12.2 Дробный факторный эксперимент
- •12.3 Метод наименьших квадратов
- •13.1 Основная цель кластерного анализа
- •13.2 Объединение (древовидная кластеризация)
- •13.3 Двувходовое объединение
- •13.4 Метод k средних
- •13.5 Алгоритм нечеткой кластеризации
- •14.1 Понятие когнитивного моделирования
- •14.2 Подсистема представления субъективной информации
- •14.3 Подсистема извлечения предпочтений эксперта
- •14.4 Подсистема обработки
- •14.5 Подсистема представления результатов моделирования
- •14.6 Подсистема поддержки аналитической деятельности эксперта
- •14.7 Моделирование бизнес процессов на основе bpmn-диаграмм
- •14.8 Метод анализа иерархий (маи): введение
- •14.9 Основные принципы маи
- •1. Принцип идентичности и декомпозиции
- •2. Принцип дискриминации и сравнительных суждений
- •3. Принцип синтеза
- •14.10 Общая оценка маи как метода принятия решений
- •15.1 Общий ход решения задачи на основе метода конечных элементов
- •15.2 Сети одномерных конечных элементов
- •15.3 Виды конечных элементов
- •16.1 Основные понятия
- •16.2 Приближенное решение оду при заданных начальных условиях
- •16.3 Метод Эйлера и его модификации
- •16.4 Метод Рунге-Кутта
- •16.5 Приближенное решение ду n-го порядка при заданных начальных условиях
- •16.6 Приближенное решение ду при заданных граничных условиях (краевых задач)
- •16.6.1 Метод начальных параметров
- •16.6.2 Редукция к задаче Коши для линейного ду второго порядка
- •17.1 Основные понятия
- •17.2 Типы элементов
- •17.3 Источники энергии и преобразователи. Аналоги топологических уравнений
- •17.4 Метод получения топологических уравнений
- •18.1 Свойства задач принятия решения со многими критериями
- •18.2. Формирование множества критериев
- •18.3 Методология решения многокритериальных задач
- •18.4 Технологии отыскания эффективных решений
- •18.5 Методы принятия решения при нескольких критериях
3. Принцип синтеза
Реализация принципа синтеза составляет содержание третьего этапа. Искомые веса объектов определяются последовательно, начиная со второго уровня иерархии в соответствии с решающим правилом
![]() (9)
(9)
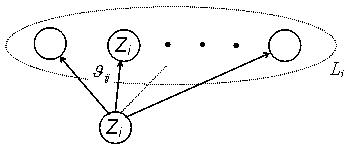
Рис. 17. Фрагмент иерархии
Веса объектов, принадлежащих уровню альтернатив, можно считать как результат измерения их в шкале отношений в диапазоне [0,1].
Согласованность всей иерархии С определяется по следующему выражению:
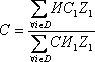 (10)
(10)
где D = I / Vm; ИСi, СИi, ‒ соответственно индекс согласованности и случайный индекс таблицы парных сравнений, рассмотренной относительно i-го объекта. Если i V1 и i > 1, то для i V1 ИСi = ИС1 и СИi = СИ1; ИС1 и СИ1 ‒ соответствующие параметры таблицы парных сравнений, которая была сформирована для определения весов объектов первого уровня.
Приемлемым является значение С меньше или равное 10%. В противном случае качество суждений следует улучшить. Возможно, следует пересмотреть формулировку вопросов при проведении парных сравнений. Если это не поможет улучшить согласованность, то, вероятно, задачу следует более точно структурировать.
14.10 Общая оценка маи как метода принятия решений
Принятие решений складывается в многодисциплинарную область исследований, в которой работают психологи, математики, программисты, экономисты, инженеры. Отметим, что эта многодисциплинарность является как бы переходным этапом к появлению новой дисциплины, в рамках которой специалисты будут обладать необходимыми научными знаниями из приведенных выше дисциплин, а также новыми знаниями по проблемам, ранее не изучавшимся.
Рассмотрим, насколько удовлетворяет МАИ ряду требований к научному обоснованию методов принятия решений:
1. В МАИ способы получения информации от ЛПР/эксперта соответствуют данным когнитивной психологии о возможностях человека перерабатывать информацию. Действительно, гомогенность и принцип иерархической декомпозиции приводят в соответствие проблему получения оценок с психометрическими возможностями человека.
2. В МАИ имеется возможность проверки информации, полученной от ЛПР/эксперта на непротиворечивость, посредством индекса и отношения согласованности как для отдельных матриц, так и для всей иерархии.
3. Любые соотношения между вариантами решений в МАИ объяснимы на основе информации, полученной от ЛПР/экспертов. Так, анализ весов объектов по нисходящим уровням иерархии позволяет понять, как получено то или иное значение веса.
4. Математическая правомочность решающего правила в МАИ прозрачна и базируется на методе собственных значений и принципе иерархической композиции, имеющих четкое математическое обоснование.
Таким образом, МАИ удовлетворяет четырем основным критериям обеспечивающим всестороннюю научную обоснованность метода принятия решений.
Решающим преимуществом МАИ над большинством существующих методов оценивания альтернатив является вклад в анализ структуры проблемы и отчетливое выражение суждений.
Сложность, как было уже отмечено, характеризуется большим числом взаимодействий между многими субъективными и объективными факторами различного типа и степени важности, а также группами людей с различными целями и противоречивыми интересами. Эти факторы определяют вероятность или невозможность выбора одной из альтернатив, которая приемлема для всех с определенной степенью компромисса.
Чтобы разобраться с этой сложностью, нужна систематическая процедура для представления групп, их целей, критериев и поведения, обусловленных этими целями, альтернативных исходов и ресурсов, распределяемых по этим альтернативам. В МАИ эта процедура сводится к построению иерархии проблемы.
Общая цель (фокус) проблемы (например, выбор наилучшего автомобиля, построение наилучшей системы, распределение ресурса в соответствии с важностью) является обычно высшим уровнем иерархии. За фокусом следует уровень наиболее важных критериев (таких, как стоимость, стиль, комфортабельность и размеры автомобиля, или же в планировании ‒ прибыльность инвестиции, конкуренция и т.д.). Каждый из критериев может разделяться на субкритерии. За субкритериями следует уровень альтернатив, число которых может быть очень большим.
Как будет показано, в некоторые иерархии может быть включен уровень действующих сил (акторов), который расположен ниже уровня общих критериев. Уровень определяет, какой из акторов наибольшим образом воздействует на исход. За этим уровнем для каждого актора следует уровень целей акторов, за которым следует уровень политик акторов, и далее уровень альтернативных исходов.
В общем, декомпозиция проблемы в иерархию зависит от хода мыслей ЛПР (его концепции решения проблемы), интуиции и опыта.
С целью иллюстрации этапов МАИ рассмотрим задачу о выборе работы.
Пример 1
Со студентом, только что получившим диплом, беседовали о трех возможных местах работы (А, Б и В). Он решил использовать МАИ для осуществления выбора. В результате первого этапа применения МАИ была получена следующая иерархия.
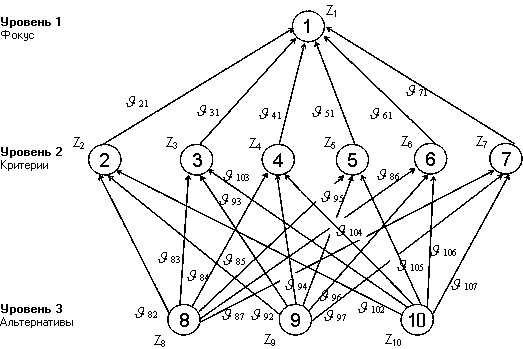
Рис. 17. Иерархия проблемы выбора работы
Уровень цели:
1. Удовлетворение работой.
Уровень критериев:
2. Исследовательская работа;
3. Рост;
4. Доходы;
5. Коллеги;
6. Местонахождение;
7. Репутация.
Уровень альтернатив:
8. А;
9. Б;
10. В.
Выполнение второго этапа связано с заполнением нижеприведенных таблиц по методу парных сравнений с применением шкалы относительной важности. В результате обработки таблиц получаем собственные вектора, которые определяют веса соответствующих дуг.
max = 6,35; ИС = 0,07; ОС = 0,06
В таблице пары критериев сравниваются с точки зрения их относительного вклада в общее понятие "удовлетворение работой". Задавался вопрос: который из заданной пары критериев представляется вносящим больший вклад в понятие "удовлетворение работой" и насколько? Например, число 5 в третьей строке и четвертом столбце показывает, что "доходы" намного важнее, чем "общество коллег".
В следующей таблице представлены результаты парных сравнений относительно соответствующих критериев.
Результатом
третьего этапа (синтеза) является
определение весов
![]() согласно
соотношению (9). Так как уровень 1 имеет
одну цель, то Z1 = 1. Отсюда:
согласно
соотношению (9). Так как уровень 1 имеет
одну цель, то Z1 = 1. Отсюда:
Z2 = 21Z1 = 0,16;
Z3 = 31Z1 = 0,19;
Z4 = 41Z1 = 0,19;
Z5 = 51Z1 = 0,05;
Z6 = 61Z1 = 0,12;
Z7 = 71Z1 = 0,30;
Вычислив веса критериев, переходим к вычислению весов альтернатив (т.е. объектов третьего уровня):
Z8 = 82Z2 + 83Z3 + 84Z4 + 85Z5 + 86Z6 + 87Z7 = 0,160,16 + 0,330,19 + 0,450,19 + 0,770,05 + 0,250,12 + 0,690,3 = 0,45
Z9 = 92Z2 + 93Z3 + 94Z4 + 95Z5 + 96Z6 + 97Z7 = 0,590,16 + 0,330,19 + 0,090,19 + 0,050,05 + 0,050,12 + 0,090,3 = 0,25
Таким образом, в конечном счете альтернатива А имеет вес 0,45, Б ‒ 0,25 и В ‒ 0,3.
Пример 2
Задача определения приоритетов отраслей промышленности. Она возникает при распределении энергии для нескольких крупных потребителей в соответствии с их общим вкладом в реализацию различных целей общества. Иерархия решения этой задачи имеет следующий вид:
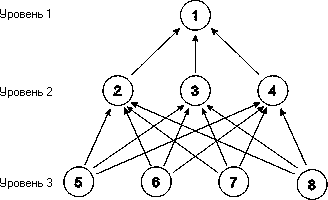
Рис. 18. Иерархия задачи определения приоритетов отраслей промышленности
Первый уровень иерархии имеет одну цель: общее благосостояние страны (1).
Второй уровень иерархии имеет три цели: сильная экономика (2), здравоохранение (3) и национальная оборона (4). Приоритеты этих целей получаются из таблицы парных сравнений относительно цели первого уровня.
Объектами третьего уровня являются отрасли промышленности (5,6,7,8). Задача заключается в определении влияния отраслей промышленности на общее благосостояние страны через промежуточный второй уровень.
Пример 3
Применение МАИ для сравнительного анализа различных технических систем. Например, необходимо осуществить оценку четырех современных систем аккумулирования энергии на основе шести критериев. Соответствующая иерархия имеет следующий вид:
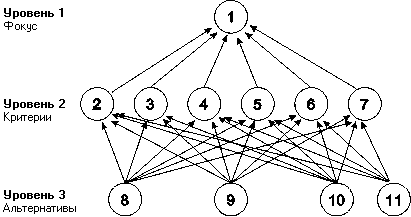
Рис. 19. Иерархия сравнительного анализа технических систем
В таблице представлены результаты парных сравнений относительно соответствующих критериев.
В качестве критериев принимались следующие:
2. Экологический.
3. Экономический.
4. Социальный.
5. Выбор места.
6. Время, требуемое для постройки.
7. Совместимость с энергосистемой.
Множество систем аккумулирования энергии включало:
8. Накопление сжатого воздуха.
9. Подземная гидроаккумуляция.
10. Электрические батареи.
11. Накопление энергии водорода.
Матрица парных сравнений к примеру 3
-
2
3
4
5
6
7
Собственный вектор
2
1
1/5
2
1/3
1/2
2
0,09
3
5
1
7
2
3
7
0,42
4
1/2
1/7
1
1/5
1/2
1
0,05
5
3
1/2
5
1
2
5
0,25
6
2
1/3
2
1/2
1
3
0,14
7
1/2
1/7
1
1/5
1/3
1
0,05
max = 6,05; ИС = 0,01; ОС = 0,01.
После проведения этапа синтеза получено следующее ранжирование аккумулирующих систем:
электрические батареи ‒ 0,36;
накопление сжатого воздуха ‒ 0,26;
накопление энергии водорода ‒ 0,24;
подземная гидроаккумуляция ‒ 0,14.
Литература
1. Ильина Н.В. Системный анализ и моделирование процессов в техносфере: Учеб. пособие / Н.В. Ильина, Д.Д. Лапшин, В.И. Федянин. – Ч. 1. Воронеж: ГОУВПО «Воронежский государственный технический университет, 2008. – 206 с.
Лекция 15. Метод конечных элементов
