3.Типовое задание «Определение параметров нелинейности усилителя аппаратуры вч связи по лэп на основе аппроксимации его коэффициента усиления и выбор оптимального режима» Задание на курсовую работу

1. Аппроксимировать полиномом седьмой степени экспериментальную зави-симость коэффициента усиления Кэ = f ( Uсм ) заданного усилительного кас-када на полевом транзисторе (ПТ) типа 2П902А (рис. 1) .

2. На основе вычисленных коэффициентов аппроксимации и гармонического анализа с использованием метода МКП по формулам (4- 5 и 9-11 ) опреде-лить параметры нелинейности третьего порядка и выбрать оптимальный режим работы каскада.

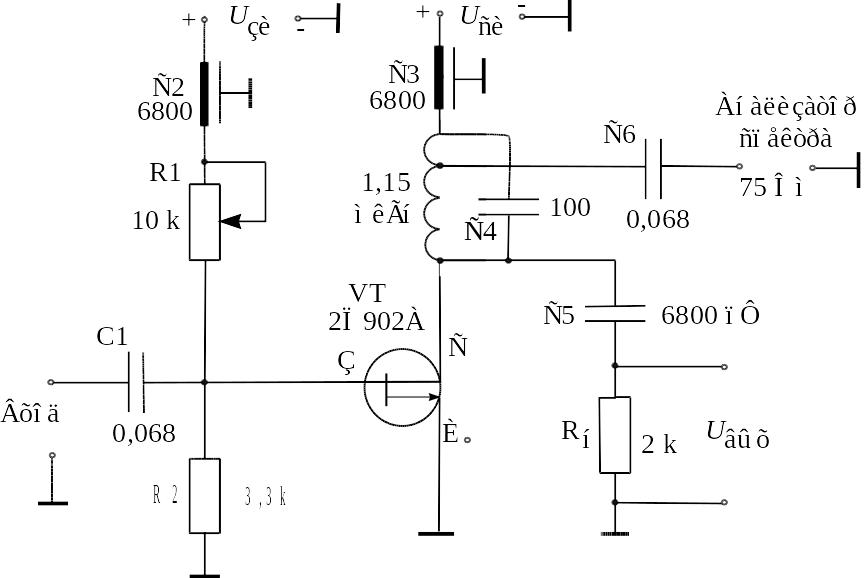
Рис. 1 . Исследуемый усилительный каскад на ПТ 2П902А

Аппроксимация [ Вариант № 2- пт 2п902а (к)]

Аппроксимацию проводим в следующей последовательности.

1. Задаем 11 экспериментальных значений коэффициента усиления в равноотстоящих точках напряжения смещения «затвор-исток» в интервале В. Эти данные, а также вспомогательные значения нечетных 2К_н и четных 2К_ч компонент коэффициента усиления в симметричных точках смещения U_зи сводим в табл. 2. ( Варианты заданий смотрите ниже – в заключительной части выполняемого задания).

Таблица 2

х	-1,0	-0,8	-0,6	-0,4	-0,2	0	0,2	0,4	0,6	0,8	1,0
Uзи	0	0,4	0,8	1,2	1,6	2,0	2,4	2,8	3,2	3,6	4,0
Кэ	0	1,6	6,6	10,9	13,9	16	17,65	18,9	19,6	20,05	20,3
2Кн	-	-	-	-	-	0	3,75	8,0	13	18,45	20,3
2Кч	-	-	-	-	-	16	31,55	29,8	26,2	21,65	20,3
В0	0,000574	1,5964132	6,605958	10,901099	13,88494	16,013656	17,65900	18,873555	19,6215	20,0416	20,3008

2. Находим коэффициенты разложения ортогональных полиномов по формулам (21) преобразовав их при N=11 в выражения (22)

,

,

.

(22)

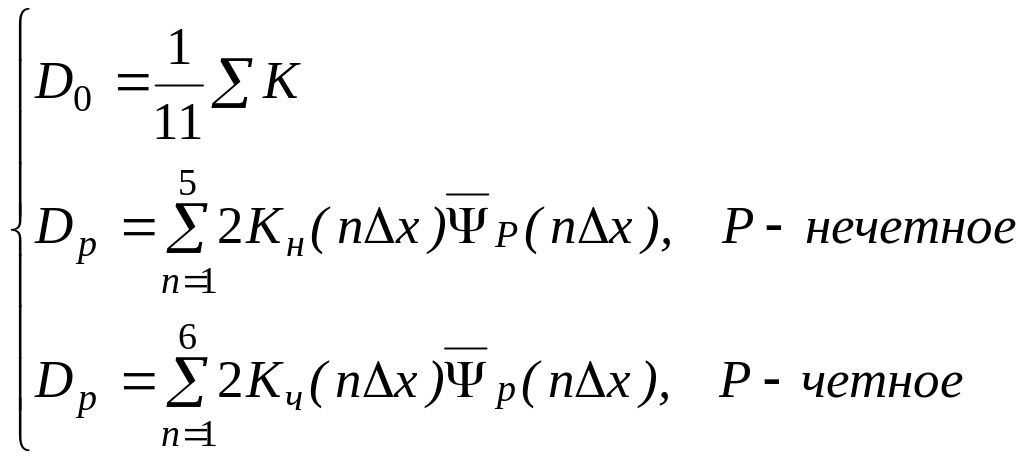
Заметим, что при определении коэффициента D₀ используется вторая формула (21), а из табл. 1 следует, что при N=11 нулевой полином для любого х имеет величину , поэтому в соответствии с формулой (18) можно найти сумму всех значений табл. 2, и поделить на 11, т. е.

.

Для определения используем первую формулу (22). Входящие в нее нечетные компоненты берем из табл. 2 (это разностные значения в симметричных точках), а значения полинома – из табл. 1

Для определения используем вторую формулу (22), в которой четные компоненты являются суммарными значениями в симметричных точках аргумента х, кроме точки х=0, в которой значение .

Аналогично находим остальные коэффициенты:

; ; ;

; ; ;

; .

Полином по степеням х находится по формуле (15), с преобразованием ее в (23), в которой аппроксимирующий полином в отличие от аппроксимируемой функции обозначен как :

, (23)

где – ортогональные полиномы.

Группируя коэффициенты по степеням х и собирая подобные члены, приходим к удобным выражениям для вычисления членов А₀, А₁х, А₂х², А₃х³ и т.д. этого полинома:

;

;

;

;

;

;

;

.

В итоге полином по степеням х:

; (24)

.

Для перевода этого полинома в истинный полином по степеням необходимо уточнить, удовлетворяют ли значения условиям трех нижеследующих формул:

- при совпадении значений и х

= 0 и х = 0 ; (25)

- при несовпадении значений и х

при = 0 … , (26)

при (27)

Примечание. Чтобы не усложнять расчет при заданном интервале сме-щений U_см = ( – U₁…– U_n ) [ формула (27)], рекомендуется перевести этот интервал смещений в интервал, заданный в формуле (26) и дальнейший расчет производить на основе полученного «нормированного» полинома относительно значений U_см = U_зи.н . = U_зи + U₁. Полученный интервал будет соответствовать формуле (26),т.е. U_зи.н = 0 … U_n. Удобно также переводить «отрицательные» («левые») интервалы U_ЗИ в симметричные нормированные интервалы с нулевыми значениями «х» и U_ЗИ. Ниже будет приведена таблица, облегчающая перевод заданных отрицательных интервалов смещений в их нормированные значения.

Рассматриваемый полином удовлетворяет требованиям формулы (26). Подставляем в (24) значение

,

получаем истинный теоретический полином В_о по степеням :

(28)

По найденному уравнению вычисляем и заносим в нижнюю графу табл. 2 значения В₀ в контрольных точках напряжения смещения .

Из сопоставления экспериментальных значений и теоретических В₀ рис. 2 видим, что совпадение очень хорошее. Абсолютная ошибка находится в пределах сотых долей, что характеризует пригодность результатов аппроксимации для дальнейшего гармонического анализа различных нелинейных явлений. В заключение отметим, что с помощью простых современных микрокалькуляторов без привлечения компьютерных программ такую аппроксимацию можно выполнить в пределах 30 минут.

Таблица нормирования некоторых реальных интервалов смещений U_ЗИ [28

Реальный интервал смещений UЗИ	Нормированный интервал UЗИ Н =	Формула нормировки
-12…….-8,5……-5,0; ∆UЗИ =0,7	UЗИ +12 = 0……3.5…….7,0	х = 2/7 UЗИ - 1.
-12…….-8,5…….-5,0; ∆UЗИ =0,7	UЗИ +8,5 = -3,5…..0……3.5	х = 2/7 UЗИ .
-5,6……-3.6……-1.6; ∆UЗИ =0,4	UЗИ +5,6 = 0…..2,0……4.0	х = 0,5 UЗИ -1
-5,6……-3.6……-1.6; ∆UЗИ =0,4	UЗИ +3,6 = -2…..0……+2,0	х = 0,5 U ЗИ.
-7.4……-5.4……-3.4; ∆UЗИ =0,4	UЗИ +7.4 = 0…..2,0……4.0	х = 0,5 UЗИ -1
-7.4……-5.4……-3.4; ∆UЗИ =0,4	UЗИ +5,4 = -2…..0……+2,0	х = 0,5 U ЗИ.