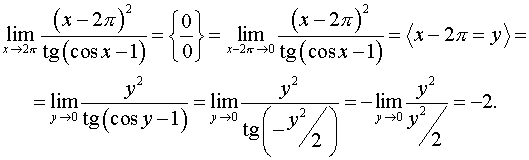Вычисление пределов вида
Постановка задачи. Вычислить предел
,
где и – бесконечно малые функции в точке .
План решения.
Способ 1. Непосредственное вычисление пределов.
В зависимости от примера необходимо воспользоваться приемом домножения числителя и знаменателя на сопряженное выражение (если в дроби присутствуют радикалы) либо одной из следующих формул, приведя предварительно выражение к соответствующему виду:
,
(первый замечательный предел),
(второй замечательный предел),
,
,
.
Во всех приведенных выше формулах при .
Способ 2. Замена на эквивалентные бесконечно малые.
1. Нужно заменить и на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки . Поэтому сначала сделаем замену переменной и будем искать предел при (если , то замену делать не надо).
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяем в произведении и частном бесконечно малые функции эквивалентными.
Таблица эквивалентных бесконечно малых:
Функция |
Эквивалентная бесконечно малая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 11. Вычислить пределы функций.
Способ 1.
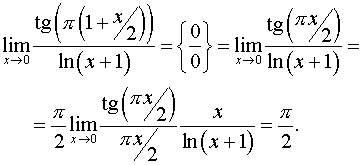
Способ 2.
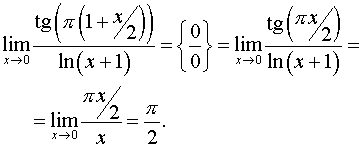
Вычисление пределов вида
Постановка задачи. Вычислить предел
,
где и – бесконечно малые функции в точке .
План решения.
Способ 1. Непосредственное вычисление пределов.
В зависимости от примера необходимо воспользоваться приемом домножения числителя и знаменателя на сопряженное выражение (если в дроби присутствуют радикалы) либо одной из следующих формул, приведя предварительно выражение к соответствующему виду:
,
(первый замечательный предел),
(второй замечательный предел),
,
,
.
Во всех приведенных выше формулах при .
Способ 2. Замена на эквивалентные бесконечно малые.
1. Нужно заменить и на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки . Поэтому сначала сделаем замену переменной и будем искать предел при (если , то замену делать не надо).
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяем в произведении и частном бесконечно малые функции эквивалентными.
Таблица эквивалентных бесконечно малых:
Функция |
Эквивалентная бесконечно малая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 12. Вычислить пределы функций.
Способ 1.
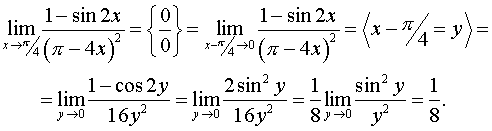
Способ 2.
Вычисление пределов вида
Постановка задачи. Вычислить предел
,
где и – бесконечно малые функции в точке .
План решения.
Способ 1. Непосредственное вычисление пределов.
В зависимости от примера необходимо воспользоваться приемом домножения числителя и знаменателя на сопряженное выражение (если в дроби присутствуют радикалы) либо одной из следующих формул, приведя предварительно выражение к соответствующему виду:
,
(первый замечательный предел),
(второй замечательный предел),
,
,
.
Во всех приведенных выше формулах при .
Способ 2. Замена на эквивалентные бесконечно малые.
1. Нужно заменить и на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки . Поэтому сначала сделаем замену переменной и будем искать предел при (если , то замену делать не надо).
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяем в произведении и частном бесконечно малые функции эквивалентными.
Таблица эквивалентных бесконечно малых:
Функция |
Эквивалентная бесконечно малая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 13. Вычислить пределы функций.
Способ 1.
Способ 2.
