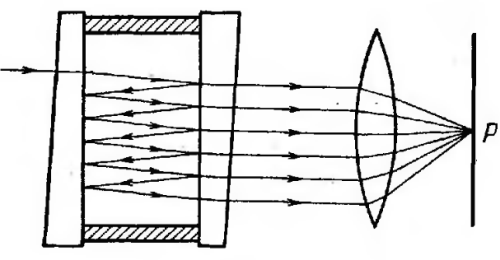
Главные плоскости и точки.
Рассмотрим две сопряжённые плоскости,
перпендикулярные к оптической оси
системы. Отрезок прямой
![]() ,
лежащий в одной из этих плоскостей,
будет иметь своим изображением отрезок
прямой
,
лежащий в одной из этих плоскостей,
будет иметь своим изображением отрезок
прямой
![]() .
Из осевой симметрии системы вытекает,
что отрезки
и
должны лежать в одной проходящей через
оптическую ось плоскости (в плоскости
рисунка). При этом изображение
может быть обращено либо в ту же сторону,
что и предмет (Рис. 6.9а), либо в противоположную
сторону (Рис. 6.9б). В первом случае
изображение называется прямым, во втором
– обратным. От
.
Из осевой симметрии системы вытекает,
что отрезки
и
должны лежать в одной проходящей через
оптическую ось плоскости (в плоскости
рисунка). При этом изображение
может быть обращено либо в ту же сторону,
что и предмет (Рис. 6.9а), либо в противоположную
сторону (Рис. 6.9б). В первом случае
изображение называется прямым, во втором
– обратным. От
|
Рис. 6.9. Отрезки и , лежащие в сопряжённых плоскостях. |
Отношение линейных размеров изображения и предмета называется линейным или поперечным увеличением:
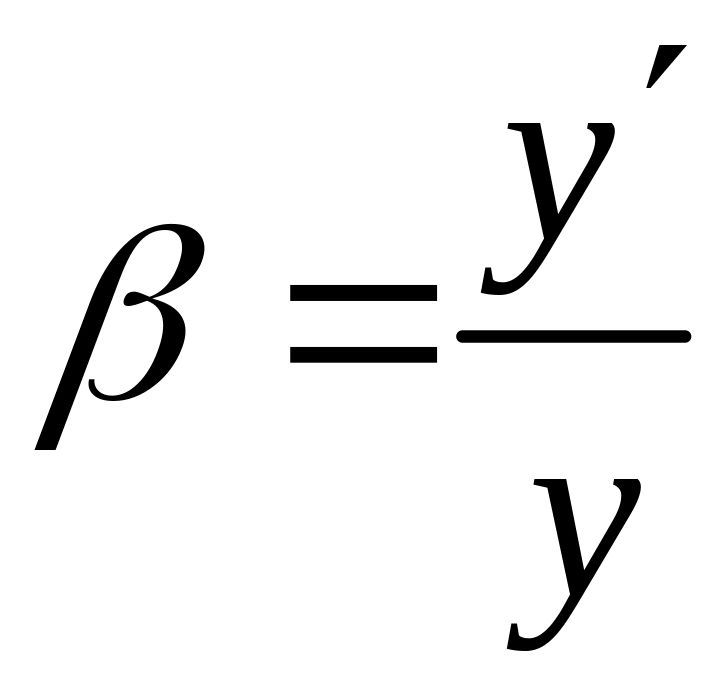 .
.
Линейное увеличение является алгебраической величиной. Оно положительно, если изображение прямое, и отрицательно, если изображение обратное.
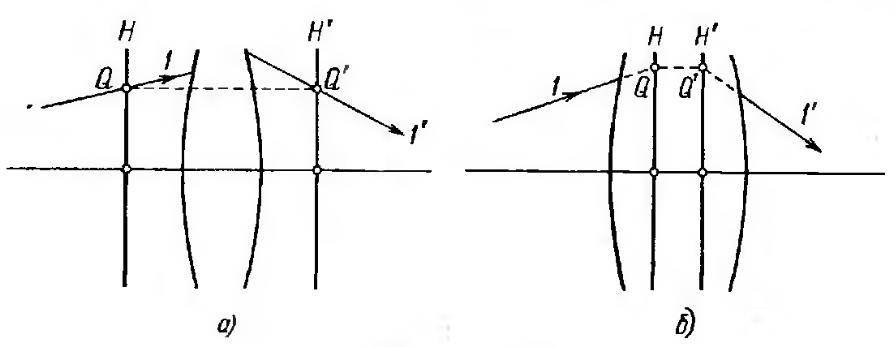
|
Рис. 6.10. Возможное расположение главных плоскостей оптической системы. |
Фокусные расстояния и оптическая сила
системы. Расстояние от передней
главной точки
до переднего фокуса
называется передним фокусным расстоянием
![]() .
Расстояние от
до
называется задним фокусным расстоянием
.
Расстояние от
до
называется задним фокусным расстоянием
![]() .
Фокусные расстояния – алгебраические
величины. Они положительны, если
соответствующий фокус лежит справа от
своей главной точки, и наоборот. Для
фокусных расстояний центрированной
оптической системы, образованной двумя
сферическими преломляющими поверхностями,
имеется соотношение:
.
Фокусные расстояния – алгебраические
величины. Они положительны, если
соответствующий фокус лежит справа от
своей главной точки, и наоборот. Для
фокусных расстояний центрированной
оптической системы, образованной двумя
сферическими преломляющими поверхностями,
имеется соотношение:
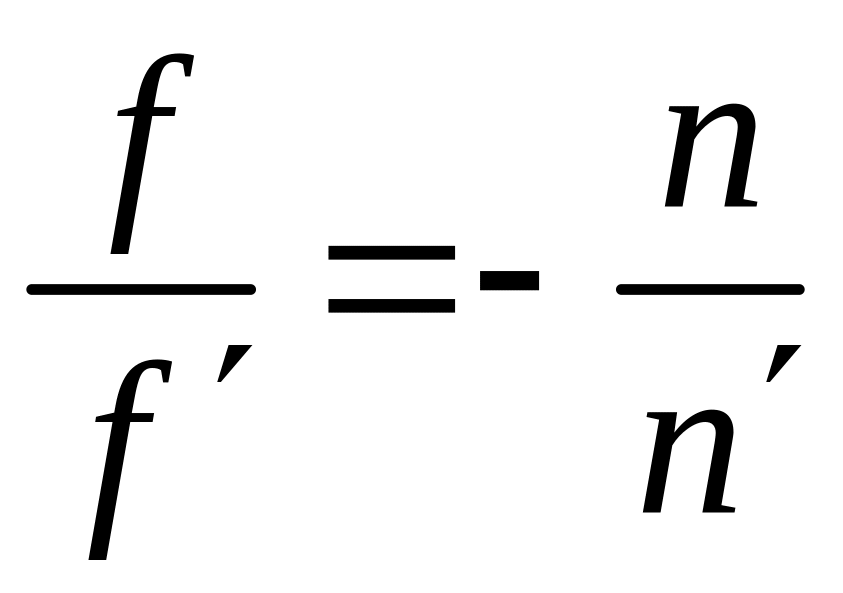 ,
,
где
- показатель преломления среды, находящейся
перед оптической системой, а
![]() - преломления среды, находящейся за
системой. При равенстве показателей
преломления слева и справа модули
фокусных расстояний равны. Величина
- преломления среды, находящейся за
системой. При равенстве показателей
преломления слева и справа модули
фокусных расстояний равны. Величина
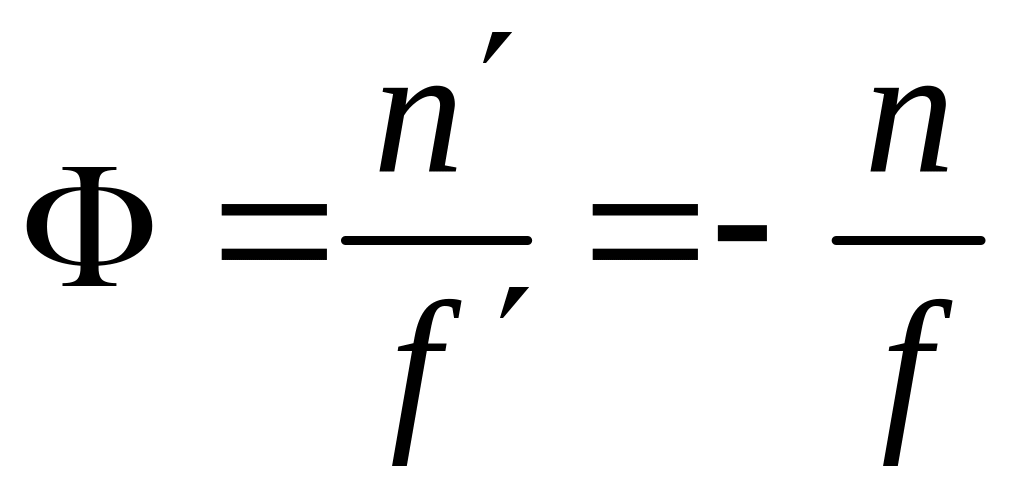
называется оптической силой системы. Чем больше , тем сильнее система преломляет лучи. Действительно, тем меньше будет фокусное расстояние, и тем меньше будет расстояние от главной плоскости до точки сбора параллельных лучей, падающих на линзу. Измеряется оптическая сила в диоптриях – 1/м.
Формула оптической системы. Задание
кардинальных плоскостей или точек
полностью определяет свойства оптической
системы. В частности, зная их расположение,
можно построить изображение предмета,
даваемое системой. Возьмём в пространстве
предметов отрезок
![]() ,
перпендикулярный к оптической оси (Рис.
6.11). Положение этого отрезка можно задать
либо расстоянием
,
перпендикулярный к оптической оси (Рис.
6.11). Положение этого отрезка можно задать
либо расстоянием
![]() от точки
от точки
![]() до точки
,
либо расстоянием
до точки
,
либо расстоянием
![]() от
до
.
Величины
от
до
.
Величины
![]() являются алгебраическими (на рисунках
указаны их модули).
являются алгебраическими (на рисунках
указаны их модули).
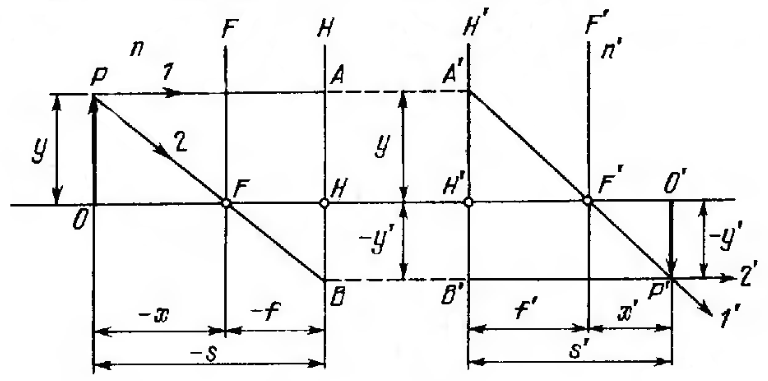
|
Рис. 6.11. Кардинальные плоскости и точки системы позволяют построить изображение предмета ОР, создаваемое ей. |
Проведём из точки
луч 1, параллельный оптической оси. Он
пересечёт плоскость
в точке
.
В соответствии со свойствами главных
плоскостей сопряжённый лучу 1 луч
![]() должен проходить через сопряжённую с
точкой
точку
должен проходить через сопряжённую с
точкой
точку
![]() .
Так как луч 1 параллелен оптической оси,
из точки
он пойдёт в точку
.
Теперь проведём из точки
луч 2, проходящий через передний фокус.
Он пересечёт плоскость
в точке
.
Так как луч 1 параллелен оптической оси,
из точки
он пойдёт в точку
.
Теперь проведём из точки
луч 2, проходящий через передний фокус.
Он пересечёт плоскость
в точке
![]() .
Сопряжённый с ним луч
.
Сопряжённый с ним луч
![]() пройдёт точку
пройдёт точку
![]() и пойдёт далее параллельно оптической
оси. Изображение точки
будет находиться на месте пересечения
лучей
и пойдёт далее параллельно оптической
оси. Изображение точки
будет находиться на месте пересечения
лучей
![]() и обозначаться
.
Изображение
и обозначаться
.
Изображение
![]() также перпендикулярно оптической оси
системы.
также перпендикулярно оптической оси
системы.
Между расстояниями
![]() имеется соотношение, называемое формулой
Ньютона:
имеется соотношение, называемое формулой
Ньютона:
![]() .
.
Из формулы легко получить соотношение
между
![]() :
:
![]() .
.
Принцип Гюйгенса-Френеля.
|
Рис.6.12. |
Интерференция света.
Пусть две ЭМВ с одинаковой частотой находятся в одной области пространства и возбуждают колебания в одной плоскости:
![]() .
.
При сложении данных волн амплитуда результирующего колебания будет подчиняться следующему выражению:
![]() ,
,
где
![]() - разность фаз. Если
- разность фаз. Если
![]() остаётся постоянной во времени, то волны
называются когерентными. В случае
некогерентных волн член, содержащий
косинус, в среднем равен нулю, и амплитуда
колебаний
будет определяться как
остаётся постоянной во времени, то волны
называются когерентными. В случае
некогерентных волн член, содержащий
косинус, в среднем равен нулю, и амплитуда
колебаний
будет определяться как
![]() .
С учётом того, что интенсивность
,
в некоторой точке пространства будет
наблюдаться простое сложение
интенсивностей. Иная картина происходит
в случае сложения когерентных волн.
Например, при
.
С учётом того, что интенсивность
,
в некоторой точке пространства будет
наблюдаться простое сложение
интенсивностей. Иная картина происходит
в случае сложения когерентных волн.
Например, при
![]() и равных амплитудах можно наблюдать
увеличение амплитуды в одних точках
пространства в два раза, а в других –
полное отсутствие поле. То есть, в
пространстве будут чередоваться
стационарные мини
и равных амплитудах можно наблюдать
увеличение амплитуды в одних точках
пространства в два раза, а в других –
полное отсутствие поле. То есть, в
пространстве будут чередоваться
стационарные мини
а) |
|
Рис. 6.13. Интерференция а) плоской волны с волной, несущей оптический вихрь; б) двух соосных пучков. |
|
|
Рис. 6.14. Интерферометр Фабри-Перо. |

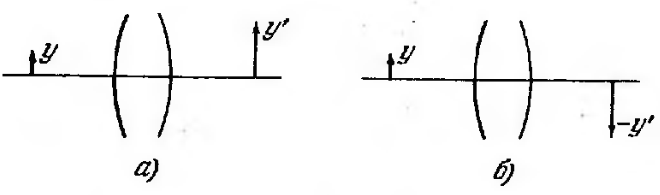


 б)
б)