Геометрическая оптика

Длины воспринимаемых глазом световых волн очень малы, поэтому распространение видимого света можно в первом приближении рассматривать, отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых линий, называемых лучами. В предельном случае, когда , законы оптики можно сформулировать на языке геометрии. Раздел оптики, в котором пренебрегают конечностью волн, называется лучевой или геометрической оптикой.

Основу лучевой оптики образуют 4-ре закона: закон прямолинейного распространения света, закон независимости световых лучей, закон отражения света, закон преломления света.

Закон прямолинейного распространения света гласит, что в однородной среде свет распространяется прямолинейно. Закон нарушается при прохождении света через препятствия, сравнимые с длиной волны.

Закон независимости световых лучей гласит, что лучи при пересечении не возмущают друг друга и распространяются независимо друг от друга. Данный закон может нарушаться при больших интенсивностях излучения в веществе, в фотонных кристаллах, где лучи могут вести себя подобно упругим телам. Законы отражения и преломления были сформулированы выше.

В основу геометрической оптики был положен принцип, установленный французским математиком Ферма в середине 17 века. Данный принцип гласит: свет распространяется по такому пути, для прохождения которого ему требуется минимальное время. Величина

называется оптической длиной пути. Принцип Ферма можно перефразировать: свет распространяется вдоль пути с минимальной оптической длиной. Из этого следует закон обратимости световых лучей – ход луча при переходе из точки А в точку Б будет точно таким же, как из точки Б в точку А.

Центрированная оптическая система

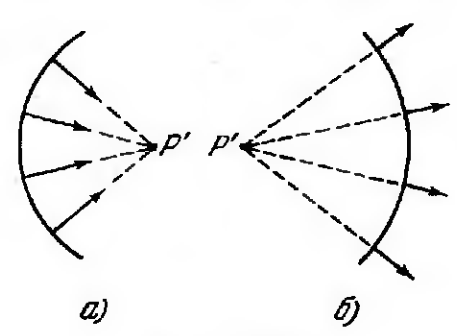
Рис. 6.6. Гомоцентрический пучок: а) сходящийся; б) расходящийся.

Совокупность лучей образует пучок. Если лучи в своём продолжении пересекаются в одной точке, пучок называется гомоцентрическим. Гомоцентрическому пучку лучей соответствует сферическая волновая поверхность (Рис. 6.6а,б). Частным случаем гомоцентрического пучка является пучок параллельных лучей, которому соответствует плоская волна. Всякая оптическая система осуществляет преобразование световых пучков. Если система не нарушает гомоцентричности пучков, то лучи, вышедшие из точки , пересекутся в точке , которая называется изображением точки . Если любая точка предмета изображается в виде точки, то изображение называется точечным, или стигматическим. Изображение называется действительным, если световые лучи в точке действительно пересекаются, и мнимым, если пересекаются их продолжения, проведённые в направлении, обратном к распространению лучей. В следствие обратимости световых лучей источник света и могут поменяться местами. Изображение источника, помещённого в , будет находиться в точке .

Оптическая система, которая даёт стигматическое изображение, геометрически подобное отображаемому предмету, называется идеальной. С помощью такой системы пространственная непрерывность точек отображается в пространственную непрерывность . Первая непрерывность точек называется пространством предметов, а вторая – пространством изображений.

Оптическая система, представляет собой совокупность отражающих и преломляющих поверхностей, отделяющих друг от друга оптически однородные среды. Обычно эти поверхности бывают сферическими или плоскими, однако возможно применение и более сложных поверхностей – эллипсоиды, гиперболоиды, параболоиды вращения. Если центры всех поверхностей лежат на одной прямой, то система называется центрированной, а данная прямая – оптической осью системы.

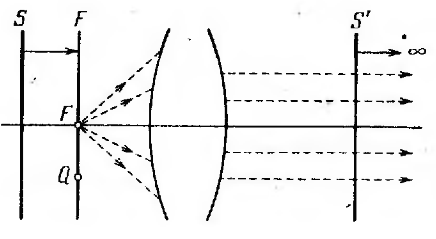
Рис. 6.7. Задняя фокальная плоскость и задний фокус.

Каждой точке или плоскости из пространства предметов соответствует точка или плоскости из пространства изображений. Среди бесконечного множества сопряжённых точек и плоскостей существуют точки и плоскости, обладающие особыми свойствами. Называются они кардинальными – фокальные, главные, узловые точки и плоскости. Задание кардинальных точек определяет свойства идеальной центрированной оптической системы.

Фокальные плоскости и фокусы оптической системы. На Рис. 6.7. показаны внешние преломляющие поверхности и оптическая ось некоторой идеальной системы. Возьмём в пространстве предметов этой системы плоскость , перпендикулярную оптической оси. Из соображений симметрии очевидно, что сопряжённая ей плоскость будет также перпендикулярна оптической оси. Перемещение плоскости на бесконечность в левую сторону вызовет смещение плоскости в положение . Плоскость называется задней фокальной плоскостью, а точка её пересечения с оптической осью – задним фокусом системы. Задний фокус системы сопряжён с точкой , лежащей на оси системы. Лучи, вышедшие из этой точки образуют параллельный пучок и собираются в заднем фокусе системы. Упавший на систему параллельный пучок может выйти из системы в виде расходящегося пучка, тогда в точке будут пересекаться не сами лучи, а их продолжения. В этом случая задний фокус окажется перед системой. Если из бесконечно удалённой точки , несовпадающей с точкой , выходит параллельный пучок, направленный под углом к оси, то они сойдутся в точке (Рис. 6.7).

Рис. 6.8. Задняя фокальная плоскость и задний фокус.

Аналогично, если удалить на бесконечность плоскость , то сопряжённая ей плоскость перейдёт в положение (Рис.6.8). Точка пересечения с оптической осью системы называется передним фокусом системы.