
- •5.4. Основные элементарные функции
- •1. Степенная функция
- •2. Показательная функция
- •3. Логарифмическая Функция
- •4. Тригонометрические функции
- •5. Обратные тригонометрические функции
- •5.5. Элементарные функции. Классификация функций. Преобразование графиков
- •5.6. Применение функций в экономике. Интерполирование функций
- •5.7. Решение задач
5.6. Применение функций в экономике. Интерполирование функций
Остановимся еще на одном важном аспекте использования функций в экономике – применении таблиц функций, которые позволяют сделать возможными различные расчеты, исключить или упростить громоздкие вычисления.
При вычислениях с помощью таблиц мы часто сталкиваемся с ситуацией, когда аргумент функции задан с большей точностью, чем позволяет таблица. В этом случае мы должны прибегнуть к интерполированию (интерполяции) – приближенному нахождению неизвестных значений функций по известным ее значениям в заданных точках.
Наиболее простым
является линейное
интерполирование,
при котором допускается, что приращение
функции пропорционально приращению
аргумента. Если заданное значение х
лежит между
приведенными в таблице значениями x0
и x1
= x0
+ h,
которым соответствуют значения
функции
![]() считают, что (рис. 5.26)
считают, что (рис. 5.26)
![]()
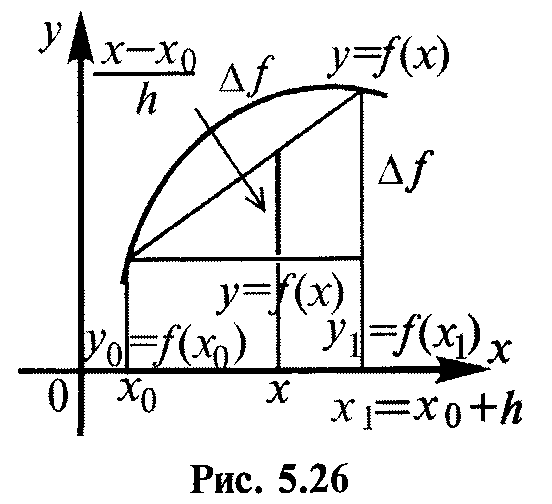
Величины
![]() называются
интерполяционными поправками.
Эти величины вычисляются с помощью
таблицы или приводятся в дополнении
к таблице.
называются
интерполяционными поправками.
Эти величины вычисляются с помощью
таблицы или приводятся в дополнении
к таблице.
Если по заданным значениям функции необходимо найти приближенное значение аргумента, то необходимо произвести обратное интерполирование.
Пример 5.4. Функция у =f(х) задана таблицей:
х |
2 |
2,04 |
2,08 |
у |
2,42 |
2,88 |
3,38 |
а) Используя линейное интерполирование, найти f(2,008).
б) Чему равен х, если f(x) =3,1?
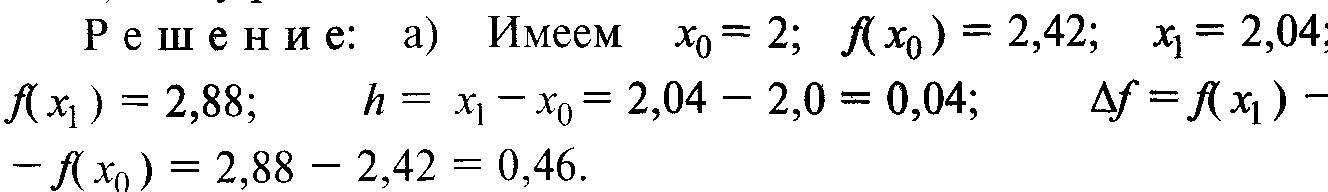
Теперь по интерполяционной формуле (5.1) получим
![]()
б) Обратное интерполирование можно провести по той же формуле, в которой поменять местами переменные х и у.
![]()
где х = (у) – неизвестное значение обратной функции.
![]()
Теперь по интерполяционной формуле (5.2) получим
![]()
В ряде случаев точность нахождения неизвестных значений с помощью линейного интерполирования оказывается недостаточной и используются другие методы интерполирования, например квадратичное интерполирование.
5.7. Решение задач
Пример 5.5. Найти область определения функций
![]()
Р е ш е н и е.
а) Область определения функции -Y найдем из системы неравенств
![]()
б) Имеем систему
![]()
Решая первое неравенство, получим 2n < х < п+2п; решая второе, найдем х2 < 4, откуда |x| 2 и –2 х 2.С помощью числовой оси (рис. 5.27) находим решение системы неравенств: 0 < х 2, т.е. область определения функции Х= (0; 2].

