Тема 6. Корреляционный анализ §1. Понятие о корреляционной связи.

В психологической практике часто возникают задачи, связанные с изучением взаимосвязей между двумя и более величинами.

Если каждому значению ставится в соответствие условная средняя, вычисленная при , то есть , то такая зависимость называется корреляционной (или корреляцией). Термин «корреляция» был введен в науку в 1886 году английским ученым Френсисом Гальтоном.

Виды корреляционной связи могут быть различны: корреляционная связь может быть линейной и нелинейной, положительной и отрицательной.

Корреляционная связь будет:

• линейной, если экспериментальные точки располагаются вдоль некоторой прямой;

• нелинейной, если экспериментальные точки располагаются вдоль какой-либо кривой, например, вдоль параболы;

• положительной, если с увеличением переменной 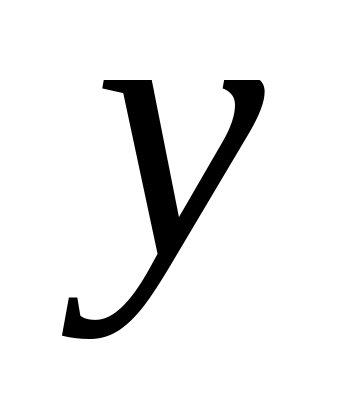переменная в среднем имеет тенденцию к увеличению;

• отрицательной, если с увеличением переменной переменная в среднем имеет тенденцию к уменьшению.

Не следует путать понятия «корреляционная связь» и «корреляционная зависимость». Зависимость – это изменение одной величины под действием другой, а корреляционная связь означает любые согласованные изменения двух величин (при этом они вполне могут не зависеть друг от друга, а зависеть от какой-то третьей величины).

Для оценки корреляционной зависимости могут использоваться различные коэффициенты: коэффициент линейной корреляции Пирсона (используется, если обе изучаемые величины распределены нормально), коэффициент ранговой корреляции Спирмена, коэффициент ранговой корреляции Кендала и другие.

§2. Коэффициент линейной корреляции Пирсона. Уравнение регрессии.

Коэффициент корреляции Пирсона используется в том случае, когда обе исследуемые величины являются количественными и распределены по нормальному закону. Данный коэффициент характеризует только наличие линейной связи. Причем, если связь между признаками имеет линейный характер, то коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому его часто называют коэффициентом линейной корреляции. Обозначается , коэффициент, вычисленный по выборке - .

Значение , вычисленное по выборке, не превышает по абсолютному значению 1 (|r_в|≤1). Чем ближе |r_в| к единице, тем теснее линейная связь. Если r_в>0, то корреляционная связь положительная. Если r_в<0, то корреляционная связь отрицательная.

Проверяется гипотеза при конкурирующей гипотезе . Наблюдаемым значением является выборочное значение коэффициента корреляции, взятое по модулю: .

Критическое значение находим по таблице критических значений коэффициента линейной корреляции: . Осуществляем выбор гипотезы, учитывая, что критерий двусторонний (но при рассматривается, как правосторонний).

Если между величинами доказана линейная корреляционная связь, то ее можно описать с помощью уравнения регрессии.

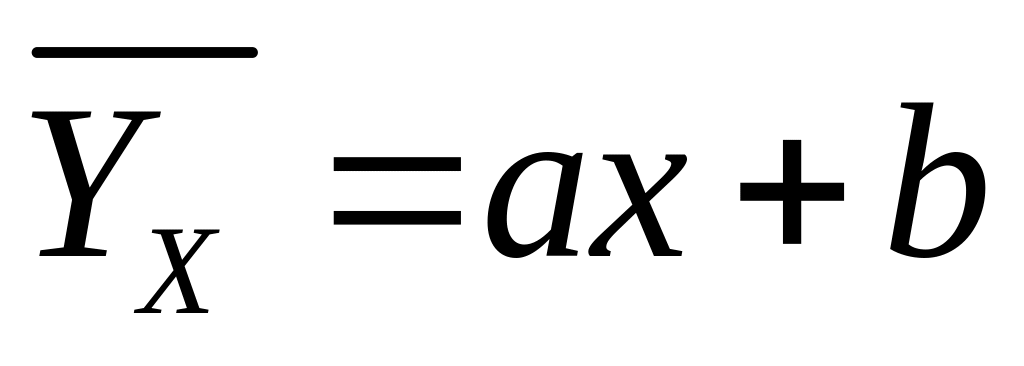• - уравнение линейной регрессии Y на Х.

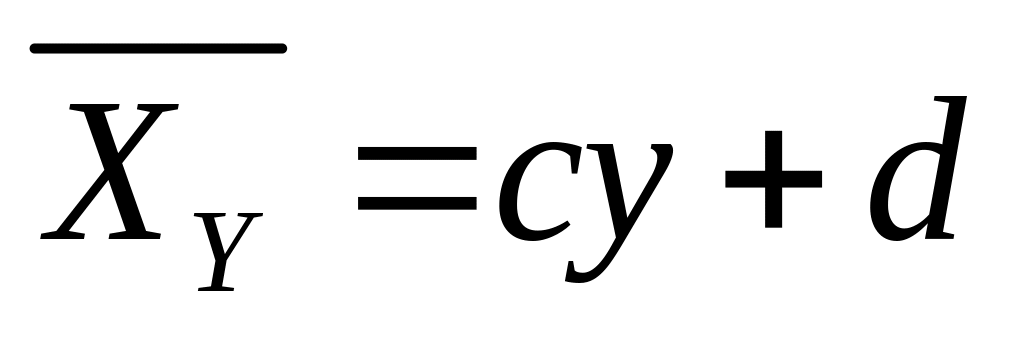• - уравнение линейной регрессии Х на Y.

Уравнение регрессии Y на Х может быть найдено по формуле: , где - коэффициент регрессии Y на Х, описывает силу линейной корреляционной связи.

Уравнение регрессии Х на Y может быть найдено по формуле:

, где - коэффициент регрессии Х на Y, описывает силу линейной корреляционной связи.

Уравнение регрессии позволяет по значению одной переменной оценить значение другой переменной.

Используется для предсказания значений, которые трудно вычислить.