Федеральное агентство по образованию

Санкт-Петербургский государственный

электротехнический университет «ЛЭТИ»

А.Д. Григорьев, В.Б. Янкевич

Электродинамика

Лабораторный практикум

Санкт-Петербург

Издательство СПбГЭТУ «ЛЭТИ»

2007

Григорьев А.Д., Янкевич В.Б.

Э61 Электродинамика: Лабораторный практикум. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2007. 80 с.

ISBN 5-230-0784-8

Изложены теоретические основы электродинамики и методика измерений основных характеристик элементов микроволновых цепей: волноводов, замедляющих систем и резонаторов. Представлена методика измерений электрофизических характеристик диэлектриков и магнетиков в микроволновом диапазоне. Основное внимание уделяется изучению электромагнитного поля в рассматриваемых устройствах и изучению таких специфических для микроволнового диапазона эффектов, как гиротропия.

Предназначено для студентов дневной и вечерней форм обучения, обучающихся по специальности 200105 (200300) – Электронные приборы и устройства направления подготовки 200100 (654100) – Электроника и микроэлектроника.

УДК 621.372.8

ББК 3.21

Рецензенты: кафедра физической электроники Санкт-Петербургского государственного политехнического университета; канд. техн. наук Г. С. Петров (ЗАО «Светлана-Электронприбор»)

Утверждено

редакционно-издательским советом университета

в качестве учебного пособия

ISBN 5-230-0784-8 СПбГЭТУ «ЛЭТИ», 2007

1. Исследование электрофизических свойств материалов в микроволновом диапазоне

Цель работы: Исследование электрофизических свойств диэлектриков и магнетиков в микроволновом диапазоне, изучение методов измерения диэлектрической и магнитной проницаемости диэлектриков и магнетиков.

1.1. Основные теоретические положения

1.1.1. Электрофизические свойства диэлектриков

При помещении диэлектрика в электрическое поле происходит его поляризация, в результате которой каждый элемент объема вещества приобретает электрический момент , где – электрические заряды частиц вещества, – их радиус-векторы, проведенные из некоторой точки отсчета, – число частиц в объеме . Большинство сред электрически нейтральны, т. е. для них , если объем много больше размера частиц. В этом случае дипольный момент не зависит от положения точки наблюдения.

Предел отношения при есть вектор электрической поляризации вещества P. Этот вектор связан с напряженностью электрического поля в веществе соотношением

где Ф/м – электрическая постоянная, – электрическая восприимчивость вещества. Изотропные среды характеризуются скалярной электрической восприимчивостью, анизотропные – тензором второго ранга

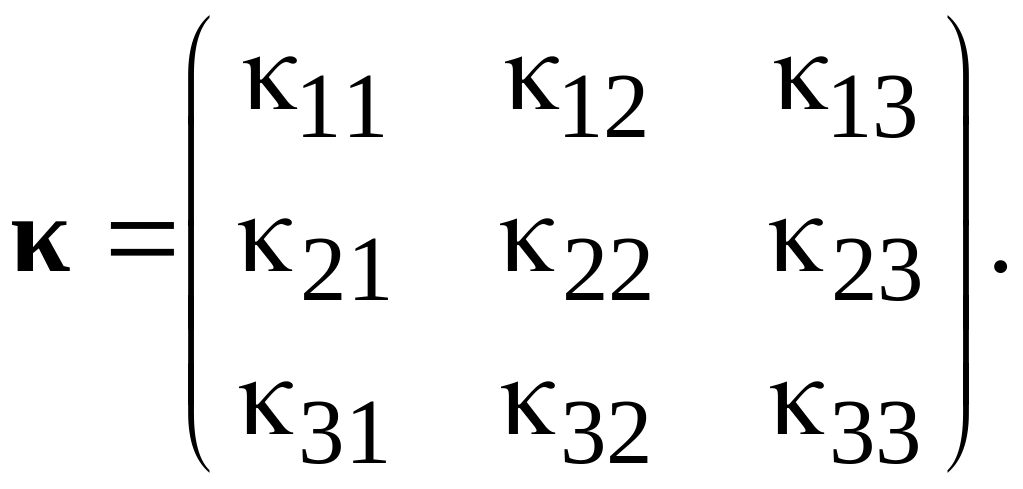
Скалярная электрическая восприимчивость (или компоненты тензора восприимчивости), вообще говоря, зависит от модуля напряженности электрического поля , радиус-вектора и ряда других физических величин. Диэлектрик называют линейным, если его электрическая восприимчивость не зависит от в рассматриваемом диапазоне значений напряженности поля, и однородным, если его электрическая восприимчивость не зависит от радиус-вектора

Вектор электрической индукции в простейшем случае определяется соотношением

Подставив в это выражение значение из формулы , найдем

где – единичный тензор (или единица для изотропной среды); – относительная диэлектрическая проницаемость; – абсолютная диэлектрическая проницаемость. В дальнейшем изложении слово «абсолютная» опускается. Диэлектрическая проницаемость – один из основных электрофизических параметров вещества.

Из формулы следует, что значение вектора в данной точке и в данный момент времени зависит от значения вектора в той же точке и в тот же момент времени, т. е. эта формула устанавливает локальную мгновенную связь между указанными векторами. В действительности на поляризацию среды требуется некоторое время, а в ряде сред вектор электрической индукции зависит от напряженности электрического поля не только в данной, но и в соседних точках. Эти явления называют временной и пространственной дисперсией среды.

С учетом дисперсии связь между векторами и определяется формулой

где – объем диэлектрического тела. Из формулы (1.4) получается (1.1), если функция имеет вид

где – дельта-функция Дирака. У большинства диэлектриков пространственная дисперсия незначительна, и ею можно пренебречь. Функция быстро убывает с ростом аргумента. В этом случае принимает вид

где – время убывания функции в раз. В соответствии с этой формулой значение вектора в данный момент времени определяется значением вектора в более ранний момент времени . Время запаздывания (постоянная диэлектрической релаксации) варьируется для различных материалов от до с.

Отметим, что в выражения – входит напряженность электрического поля внутри диэлектрика (внутреннее поле) , отличающаяся от «внешнего» поля , в которое был помещен диэлектрик. Внутреннее поле зависит от формы диэлектрического тела и его ориентации относительно внешнего поля. В общем случае внутреннее поле неоднородно даже при помещении тела в однородное внешнее поле, и его расчет достаточно сложен. Однако в некоторых телах правильной формы, помещенных в однородное поле, внутреннее поле также однородно. Так, для шара

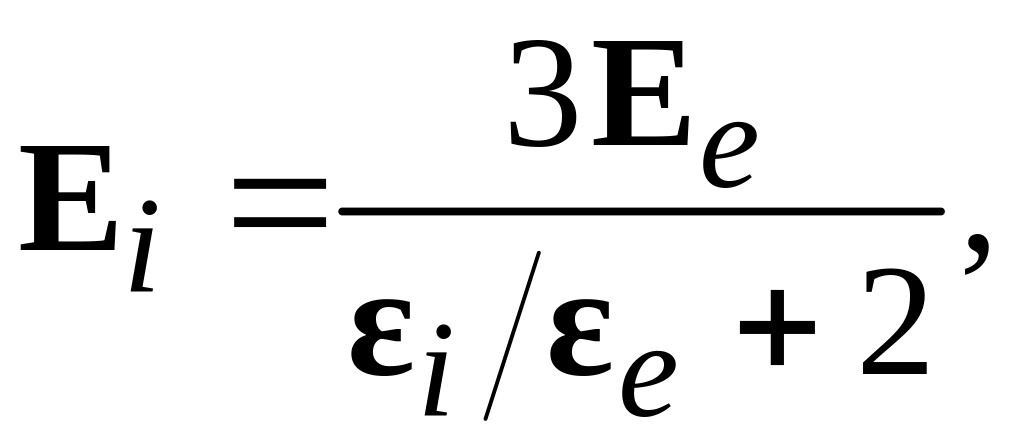
где и диэлектрические проницаемости шара и окружающего пространства. В бесконечно длинном цилиндре, ось которого совпадает с направлением внешнего поля, напряженность внутри цилиндра Если внешнее поле направлено перпендикулярно оси цилиндра, то

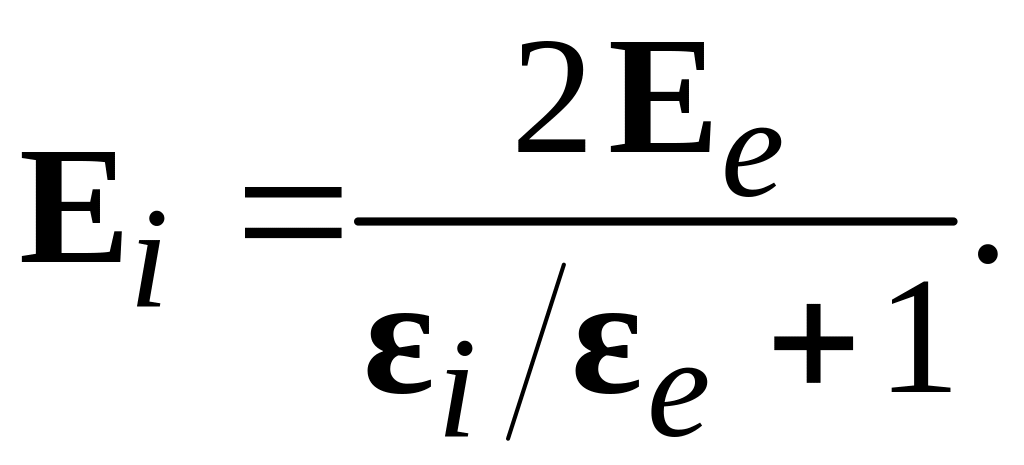
Если диэлектрик помещен в переменное электрическое поле, меняющееся во времени по гармоническому закону, то напряженность этого поля подчиняется закону , где – комплексная амплитуда; – круговая частота. Такой диэлектрик характеризуется комплексной скалярной или тензорной диэлектрической проницаемостью , где и – действительные числа, определяемые следующими выражениями:

Таким образом, комплексная диэлектрическая проницаемость учитывает, как проводимость среды , так и ее временную дисперсию.