
- •Методичні рекомендації до вивчення дисціпліни "Комп’ютерне моделювання електронних схем, конструкцій та технологій електронних апаратів"
- •1.Загальні питання
- •2.Визначення полюсів схемних функцій
- •2.1.Метод дихотомії
- •2.2.Метод хорд
- •2.3.Метод дотичних
- •2.4.Пошук комплексних коренів нелінійних рівнянь
- •3.Визначення коефіціентів чутливості
- •3.1.Розрахунок перших частинних похідних функції
- •3.1.1.Схема 2т чисельного диференціювання
- •3.1.2.Схема 3т чисельного диференціювання
- •3.2.Розрахунок власних частинних похідних другого порядку
- •3.3.Розрахунок взаємних похідних другого порядку
- •4.Визначення міри відповідності характеристик реа
- •4.1.Метод прямокутників
- •4.2.Метод трапецій
- •4.3.Метод Симпсона
- •5.Модедювання радіоелектронних апаратів системами рівнянь
- •5.1.Метод Гауса
- •5.1.1.Розв’язання систем алгебраїчних рівнянь методом Гауса
- •5.1.2.Обчислення визначника матриці методом Гауса
- •5.1.3.Обернення матриці методом Гауса
- •5.2.Метод Жордана
- •5.2.1.Обернення матриці методом Жордана
- •5.3.Метод lu-факторизації
- •5.4.Метод опорного елементу
- •6.Ітераційні методи розвяЗувАння систем лінійних рівнянь
- •6.1.Метод Якобі
- •6.2.Метод Гауса-Зейделя
- •6.3.Метод послідовної верхньої релаксації
- •7.Моделюванні статичного режиму радіоелектронних засобів
- •7.1.Метод простої ітерації
- •7.2.Метод Ньютона
- •2.3 Метод продовження параметру
- •8.Інтерполяція та наближення кривими
- •8.1.Метод невизначених коефіціентів
- •8.2.Регресійний аналіз. Метод найменших квадратів
- •8.2.1.Лінійна регресія
- •8.2.2.Квадратична регресія
- •9.Розв’язання звичайних диференційних рівнянь
- •9.1.Постановка задачі
- •9.2.Метод Ейлера
- •9.3.Метод Ейлера-Коші
- •9.4.Метод Рунге-Кутта
- •Перелік літератури
8.2.2.Квадратична регресія
Квадратична регресія - це
наближення (згладжування) експериментальних
даних квадтичним тричленом
![]()
Частинні
похідні зглажувальної функції
![]() .
Тоді допоміжна система рівнянь набуває
вигляду:
.
Тоді допоміжна система рівнянь набуває
вигляду:
|
(8.6) |
З
додатковими до раніше введених
позначеннями
![]() ;
;
![]() система
рівнянь (8.6) має вигляд:
система
рівнянь (8.6) має вигляд:
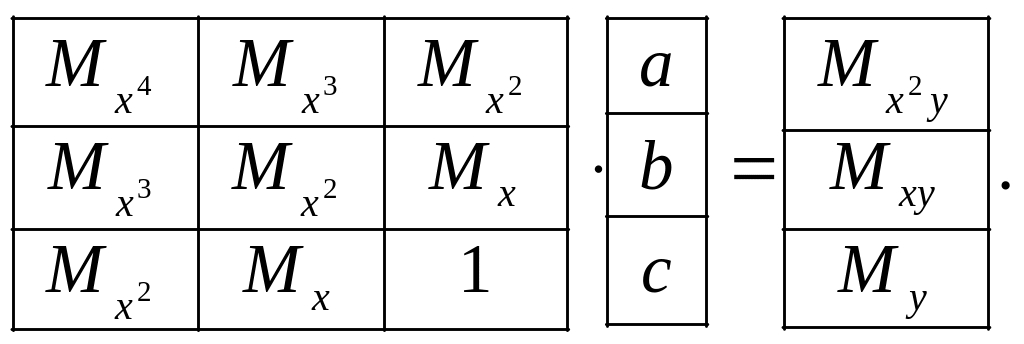
Розв’язання
системи і дозволяє отримати коефіцієнти
![]() і
побудувати
згладжувальну функцію.
і
побудувати
згладжувальну функцію.
Задача
8.4. Побудувати
згладжувальну функцію другого порядку
![]() для
виміряних
даних, що наведені в таблиці.
для
виміряних
даних, що наведені в таблиці.
хi = |
0 |
1 |
2 |
3 |
. |
уi = |
1 |
4 |
9 |
16 |
Розв’язок. Кількість змінних m=3, кількість експериментальних точок n =4.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким чином, допоміжна розширена система рівнянь для задачі має вигляд:

В
результаті розвязання
системи рівнянь а=1,
b=2,
с=1.
Тоді
згладжувальна функція буде мати вигляд
![]() Розрахунки
похибки апроксимації наведені в таблиці.
Розрахунки
похибки апроксимації наведені в таблиці.
хi = |
0 |
1 |
2 |
3 |
. |
уi = |
1 |
4 |
9 |
16 |
|
|
1 |
4 |
9 |
16 |
|
|
0 |
0 |
0 |
0 |
Згладжувальна функція точно проходить через задані точки – всі чотири точки знаходяться на параболі.
9.Розв’язання звичайних диференційних рівнянь
Деякі наукові або інженерні задачі вимагають розв’язання диференціальних рівнянь. Найпростіші з них можна розв’язати аналітично. Однак більшість задач з диференціальними рівняннями може бути розв’язана лише чисельно.
9.1.Постановка задачі
Найпростішим звичайним диференційним рівнянням є рівняння 1-го порядку вигляду:
y’=f(x, y) |
(9.1) |
Задача Коші – знайти розв’язок рівняння (6.1) у вигляді функції y(x), що задовольняє початковій умові
y(xо)= yо |
(9.2) |
Геометрично це означає, що треба знайти інтегральну криву y=y(x), що проходить через задану точку Мо(xо, yо) при виконанні рівності (6.1).

Рис.9.1. До постановки задачі
Розроблено чимало способів знаходження аналітичного розв’язання диференційних рівнянь [7]. Але часто при розв’язанні практичних задач ці методи або зовсім безпомічні, або їх розв’язання пов’язане з неприпустимими витратами зусиль та часу. Тому в пригоді стають методи наближеного розв’язання диференційних рівнянь.
9.2.Метод Ейлера
Найпростішим методом чисельного розв’язання диференційного рівняння є метод ламаних Ейлера. Нехай дано рівняння (9.1) з початковими умовами (9.2). Вибравши достатньо малий крок h, будують , починаючи з точки хо, систему рівновіддалених точок хі = хо+kh (k=0, 1, 2, …). Замість інтегральної кривої, що шукають на відрізку [x0, x1], розглядають відрізок дотичної L1 до неї в точці Мо(хо, уо) із рівняння y=y0+f(x0, y0)(x-x0). Аналогічно проводячи дотичну L2 до деякої інтегральної кривої в точці М1(х1, у1), отримують y=y1+f(x1, y1)(x-x2), і т.д.
Таким чином, ітераційні формули для розрахунку аргументу і функції для k-ої ітерації (k = 1, 2, 3, ...) мають вигляд:
хk = х0 + kh; у k уk-1 + hу' = уk-1 + 0.1(5- уk-1). |
(9.3) |
Задача 9.1. Методом Ейлера розв’язати рівняння у' = (5 - у) з початковим значенням змінної х0=0 і кроком інтегрування h =0,1.
Розв’язок. У відповідності до (9.3) для k=1 та k=2:
k=1: х1=0.1; у1 = у0 + hf(x0, y0) = 0+0,1(5-0)=0,5;
k=2: х2=0.2; у2 = у1 + hf(x1, y1) = 0.5+0.1(5-0.5)=0,95; …
Декілька кроків розвязання задачі наведено у таблиці:
k |
хk |
уk-1 |
0.1(5- уk-1) |
уk |
yт |
, % |
1 |
0,1 |
0 |
0,5 |
0,5 |
0,4758 |
5,04 |
2 |
0,2 |
0,5 |
0,45 |
0,95 |
0,9063 |
4,85 |
3 |
0,3 |
0,95 |
0,405 |
1,355 |
1,2959 |
4,55 |
… |
… |
… |
… |
… |
… |
… |
8 |
0,8 |
2,609 |
0,2391 |
2,848 |
2,7534 |
3,45 |
9 |
0,9 |
2,848 |
0,2152 |
3,063 |
2,9672 |
3,24 |
10 |
1,0 |
3,063 |
0,1937 |
3,257 |
3,1606 |
3,04 |
Точне значення ут функції отримано із аналітичного розвязку у = 5(1‑е-t) згаданого диференційного рівняння.
М етод
Ейлера забезпечує порівняно невисоку
точність [5] розрахунку (h2),
до того ж, у загальному випадку похибка
кожного нового кроку систематично
накопичується. Для оцінки похибки в
цьому випадку широко використовується
спосіб подвійного розрахунку – з кроком
h
та
h/2.
Співпадіння старших
десяткових знаків в
результатах, отриманих цими двома
способами, дає грунт вважати їх вірними.
етод
Ейлера забезпечує порівняно невисоку
точність [5] розрахунку (h2),
до того ж, у загальному випадку похибка
кожного нового кроку систематично
накопичується. Для оцінки похибки в
цьому випадку широко використовується
спосіб подвійного розрахунку – з кроком
h
та
h/2.
Співпадіння старших
десяткових знаків в
результатах, отриманих цими двома
способами, дає грунт вважати їх вірними.
Задача 9.2. Для попередньої задачі розрахувати значення уk для tk = 0,1 з кроком h=0,05.
Розв'язок. Результати розрахунків наведені в таблиці:
k |
tk |
уk-1 |
0.05(5- уk-1) |
уk |
ут |
, % |
1 |
0,05 |
0 |
0,25 |
0,25 |
0,244 |
2,46 |
2 |
0,1 |
0,25 |
0,2375 |
0,4875 |
0,476 |
2,42 |
Похибка 0,05 для кроку 0,05 і tk = 0,1 зменшилася вдвоє порівняно з порхибкою 0,1 для кроку 0,1. Ці результати відрізняються на 2,5%, що співвимірно з похибками 0,1 та 0,05.
Задача 9.3. Для задачі (4.1) розрахувати методом Ейлера два значення уk для tk = 0,05 з кроком h=0,025.
Розв'язок. Результати розрахунків наведені в таблиці:
k |
tk |
уk-1 |
0.025(5- уk-1) |
уk |
ут |
, % |
1 |
0,025 |
0 |
0,125 |
0,125 |
0,1235 |
1,21 |
2 |
0,050 |
0,125 |
0,121875 |
0,247 |
0,244 |
1,23 |
Похибка 0,025 для кроку 0,025 і tk = 0,05 зменьшилася вдвоє порівняно з похибкою 0,05 для кроку 0,05. Ці результати відрізняються на 1,2%, що співвимірно з похибками 0,025 та 0,05.

 .
.