
- •Методичні рекомендації до вивчення дисціпліни "Комп’ютерне моделювання електронних схем, конструкцій та технологій електронних апаратів"
- •1.Загальні питання
- •2.Визначення полюсів схемних функцій
- •2.1.Метод дихотомії
- •2.2.Метод хорд
- •2.3.Метод дотичних
- •2.4.Пошук комплексних коренів нелінійних рівнянь
- •3.Визначення коефіціентів чутливості
- •3.1.Розрахунок перших частинних похідних функції
- •3.1.1.Схема 2т чисельного диференціювання
- •3.1.2.Схема 3т чисельного диференціювання
- •3.2.Розрахунок власних частинних похідних другого порядку
- •3.3.Розрахунок взаємних похідних другого порядку
- •4.Визначення міри відповідності характеристик реа
- •4.1.Метод прямокутників
- •4.2.Метод трапецій
- •4.3.Метод Симпсона
- •5.Модедювання радіоелектронних апаратів системами рівнянь
- •5.1.Метод Гауса
- •5.1.1.Розв’язання систем алгебраїчних рівнянь методом Гауса
- •5.1.2.Обчислення визначника матриці методом Гауса
- •5.1.3.Обернення матриці методом Гауса
- •5.2.Метод Жордана
- •5.2.1.Обернення матриці методом Жордана
- •5.3.Метод lu-факторизації
- •5.4.Метод опорного елементу
- •6.Ітераційні методи розвяЗувАння систем лінійних рівнянь
- •6.1.Метод Якобі
- •6.2.Метод Гауса-Зейделя
- •6.3.Метод послідовної верхньої релаксації
- •7.Моделюванні статичного режиму радіоелектронних засобів
- •7.1.Метод простої ітерації
- •7.2.Метод Ньютона
- •2.3 Метод продовження параметру
- •8.Інтерполяція та наближення кривими
- •8.1.Метод невизначених коефіціентів
- •8.2.Регресійний аналіз. Метод найменших квадратів
- •8.2.1.Лінійна регресія
- •8.2.2.Квадратична регресія
- •9.Розв’язання звичайних диференційних рівнянь
- •9.1.Постановка задачі
- •9.2.Метод Ейлера
- •9.3.Метод Ейлера-Коші
- •9.4.Метод Рунге-Кутта
- •Перелік літератури
5.2.1.Обернення матриці методом Жордана
Методом Жордана може бути використаний для обернення матриці. Для цього розвязується система рівнянь з кількома стовпчиками вільних членів вигляду АХ = Е, де Х=А-1 – сукупність стовпчиків оберненої матриці.
Задача 5.6. Методом Жордана виконати обернення матриці із задачі 5.1.
Розв’язок. Нормування рівняння та перетворення матриці А для k =1:

Нормування другого рівняння та перетворення для k =2:

Нормування третього рівняння та перетворення матриці для k =3:
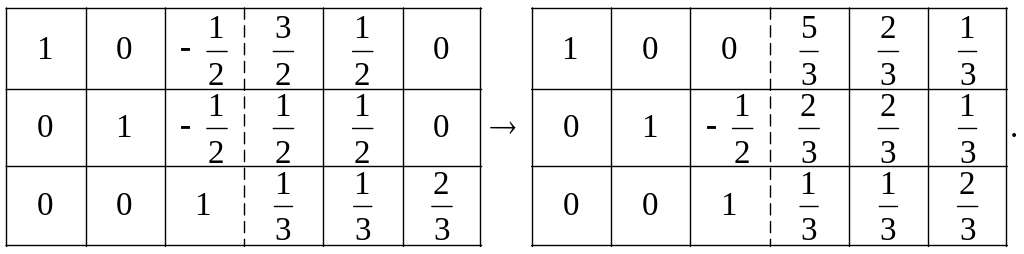
Таким чином, обернена відносно А матриця має вигляд:

що відповідає результату, отриманому раніше методом Гауса.
Програма Jordan_ов, що реалізує метод Жордана для обернення матриці із задачі 5.6 наведена нижче:
Program Jordan_ов;
uses CRT;
const n=3;
A: array [1..n,1..2*n] of real=(( 1, -1, 0, 1, 0, 0),
(-1, 3, -1, 0, 1, 0),
( 0, -1, 2, 0, 0, 1));
var i,j,k: integer;
g: real;
BEGIN
ClrScr;
for i:=1 to n do { 1. виведення початковоi матрицi }
begin
for j:=1 to 2*n do write(a[i,j]:7:2);
writeln
end;
for k:=1 to n do { 2. Jordan }
begin g:=a[k,k];
for j:=k to 2*n do a[k,j]:=a[k,j]/g;
for i:=1 to n do
if i<>k then
begin g:=a[i,k];
for j:=k to 2*n do a[i,j]:=a[i,j]-g*a[k,j];
end;
end;
writeln;
for i:=1 to n do { 3. виведення перетвореноi матрицi }
begin
for j:=1 to 2*n do write(a[i,j]:7:2);
writeln
end;
readln
END.
Результати виконання програми Jordan_ов обернення матриці методом Жордана мають вигляд:
1.00 -1.00 0.00 1.00 0.00 0.00
-1.00 3.00 -1.00 0.00 1.00 0.00
0.00 -1.00 2.00 0.00 0.00 1.00
1.00 0.00 0.00 1.67 0.67 0.33
0.00 1.00 0.00 0.67 0.67 0.33
0.00 0.00 1.00 0.33 0.33 0.67
Це відповідає раніше отриманим результатам.
5.3.Метод lu-факторизації
Метод LU-факторизації (LU-розкладання) грунтується на відображенні матриці коефіфціентів початкової системи рівнянь AX=B (det A 0) у вигляді L(UX)=B, де L і U – відповідно верхня та нижня трикутні матриці, і розвязання двох спрощених систем рівнянь LZ=B і UX=Z. Метод забезпечує можливість багатоваріантного аналізу з однією матрицею коефіціентів системи і різними стовпчиками вільних членів. В деяких випадках метод LU-розкладання забезпечує більш точне розвязання системи рівнянь, ніж метод Гауса [7, 9].
Нехай
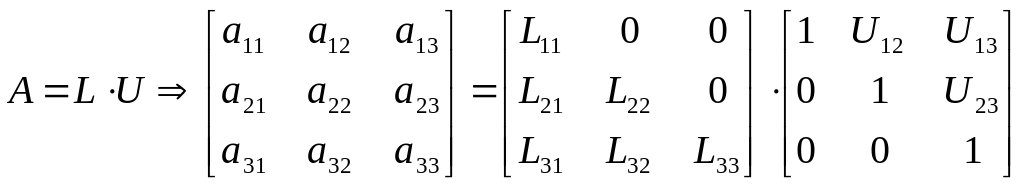 .
.
Таким чином:
a11 = L11 |
a12 = L21U12 |
a13 = L11U13 |
a21 = L21 |
a22 = L21U12 + L22 |
a23 = L21U13 + L22U23 |
a31 = L31 |
a32 = L31U12 + L32 |
a33 = L31U13 + L32U23+ L33 |
Із співставлення коефіціентів випливають формули розрахунку елементів матриць L i U:
|
(5.5) |
Розвязання систем LZ=B i UX=Z виконується відповідно формулам:
|
(5.6) |
Задача 5.7. Методом LU-факторизації розвязати систему рівнянь АХ=В, де
Розв’язок. Відповідно до (5.5) коефіцієнти матриць L і U:
L11= a11 = 1; |
u12 = a12 /L11 = = -1/1 = -1; |
u13 = a13/L11 = 0/1 = 0; |
L21= a21= -1; |
L22= a22- L21U12= = 3–(-1)(-1)= 2; |
u23 = (a23 – L21U13)/L22 = =(-1 –(-1)0)/2= -1/2; |
L31= a31= 0; |
L32= a32- L31U12 = = -1 -0(-1)= -1; |
L33= a33- L31U13- L32U23 = =2- 00–(-1)(-1/2)= 3/2; |
Таким чином, в результаті перетворення:
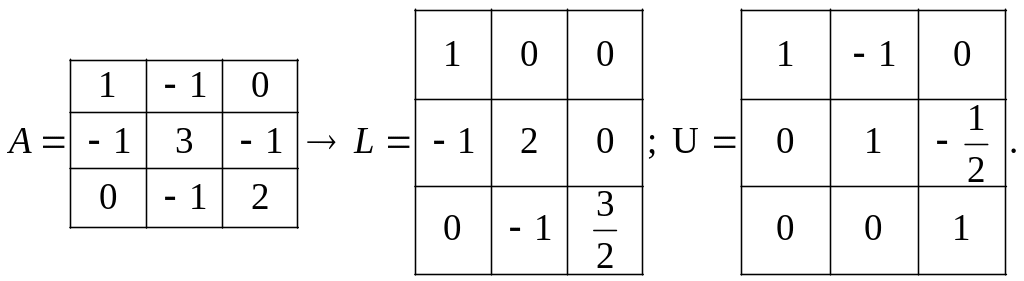
Cистемa LZ = B має вигляд:
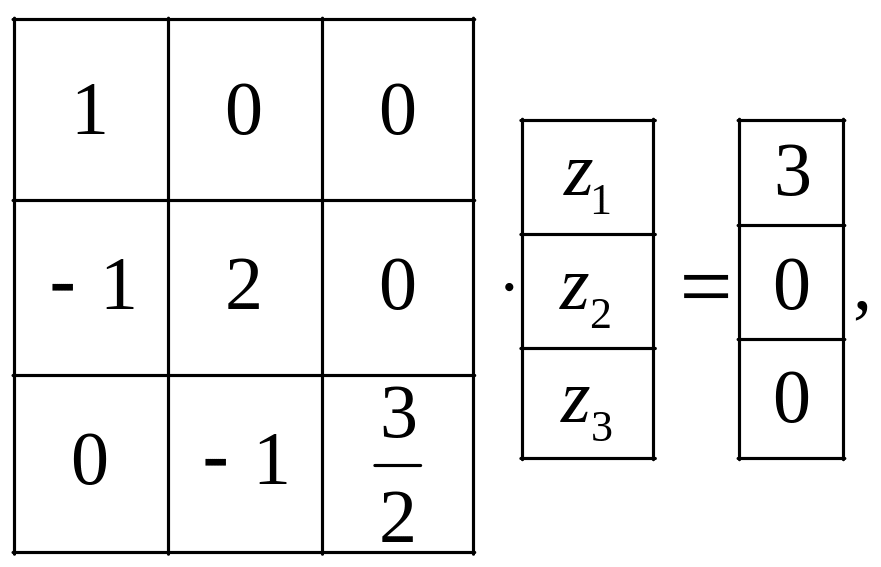
а її розвязок відповідно до (5.6):
z1= b1 /L11 = 3 /1 = 3;
z2= (b2-L21z1 )/L22 = (0-(-1)3 )/2 = 3/2;
z3= (b3-L31z1-L32z2)/L33 = (0-03-(-1)3/2)/(3/2)= 1.
Cистемa UХ= Z має вигляд:
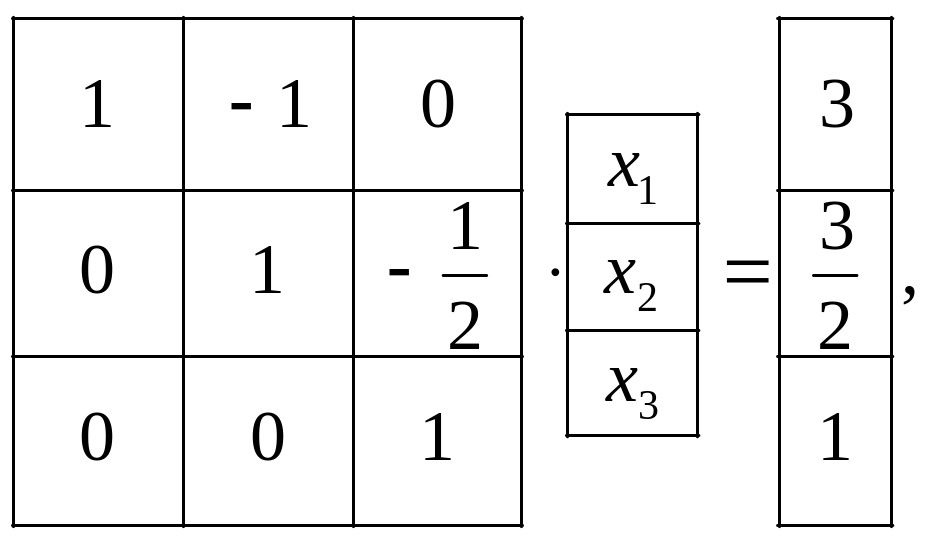
а її розвязок відповідно до (5.6):
х3= х2= х1= |
z3 z2- u23z3 = z1- u12z2-u13z3 = |
= 3/2-(-1/2)1 = 3-(-1)2- 01 = |
1; 2; 5. |
Таким чином, отриманий загальний
розвязок
![]() системи
рівнянь співпадає з її розвязком
за методом Гауса.
системи
рівнянь співпадає з її розвязком
за методом Гауса.
Програма LU_fact, що реалізує метод LU-факторизації для розв’язання системи рівнянь із задачі 5.7, наведена нижче:
Program LU_fact;
uses CRT;
const
a: array [1..3,1..3] of real = (( 1,-1, 0),
(-1, 3,-1),
( 0,-1, 2));
b: array [1..3] of real = ( 3, 0, 0);
n=3;
var z, x: array [1..3] of real;
s:real;
i, j, k: integer;
BEGin
clrscr; writeln(' A|B-matrix:');
for i:=1 to n do { 1. Print AB-matrix }
begin for j:=1 to n do write( a[i][j]:9:6);
writeln( b[i]:11:6);
end;
for i:=1 to n do { 2. Factorisation }
for j:=1 to n do
if(i>=j) then
begin s:=0;
for k:=1 to j-1 do s:=s+a[i][k]*a[k][j];
a[i][j]:=a[i][j]-s;
end else
begin s:=0;
for k:=1 to i-1 do s:=s+a[i][k]*a[k][j];
a[i][j]:=(a[i][j]-s)/a[i][i];
end;
writeln; writeln(' LU|B-matrix:');
for i:=1 to n do { 3. Print LU-matrix}
begin for j:=1 to n do write(a[i][j]:9:6);
writeln( b[i]:11:6);
end;
writeln;
for i:=1 to n do { 4. LZ=B}
begin s:=b[i];
for j:=1 to i-1 do s:=s-a[i][j]*z[j];
z[i]:=s/a[i][i];
writeln('z', i, '=', z[i]:6:3);
end;
writeln; { 5. UX=Z }
for i:=n downto 1 do
begin s:=z[i];
for j:=i+1 to n do s:=s-a[i][j]*x[j];
x[i]:=s;
writeln('x', i, '=', x[i]:6:3);
end;
readln;
END.
Результати виконання програми LU_fact наведені нижче:
A|B-matrix:
1.000000 -1.000000 0.000000 3.000000
-1.000000 3.000000 -1.000000 0.000000
0.000000 -1.000000 2.000000 0.000000
LU|B-matrix:
1.000000 -1.000000 0.000000 3.000000
-1.000000 2.000000 -0.500000 0.000000
0.000000 -1.000000 1.500000 0.000000
z1=3.000000
z2=1.500000
z3=1.000000
x3=1.000000
x2=2.000000
x1=5.000000
Результати розв’язання системи співпадають із отриманими раніше.

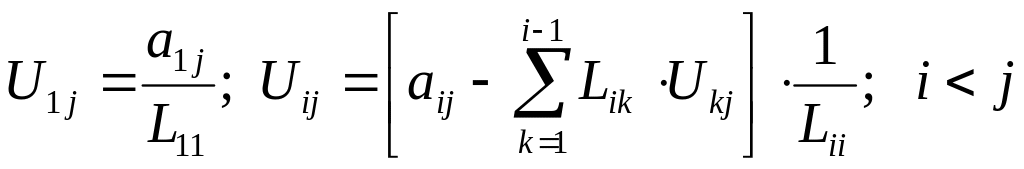 .
.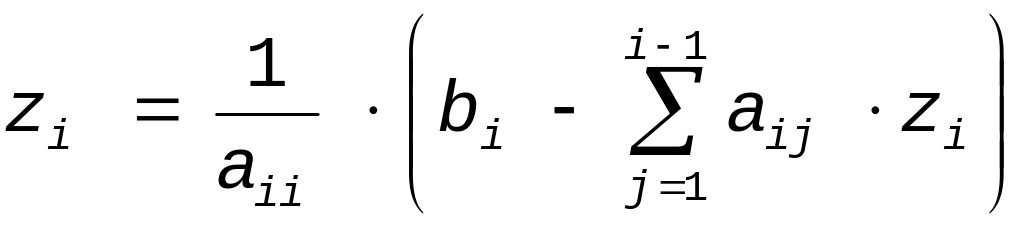 ;
;
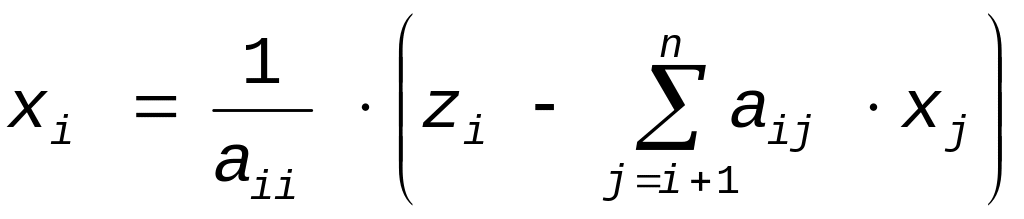 .
.