Вопросы и ответы по курсу

«Техника защиты окружающей среды» Часть 1. 10.04.12.

1. Очистка газов и воздуха от посторонних примесей

1.1. Очистка газов и воздуха от аэрозольных частиц

1.1.1. Функции распределения аэрозольных частиц по размерам

1. На графиках (а) и (в) изображены по экспериментальным данным гистограммы распределения аэрозольных частиц по их размерам.

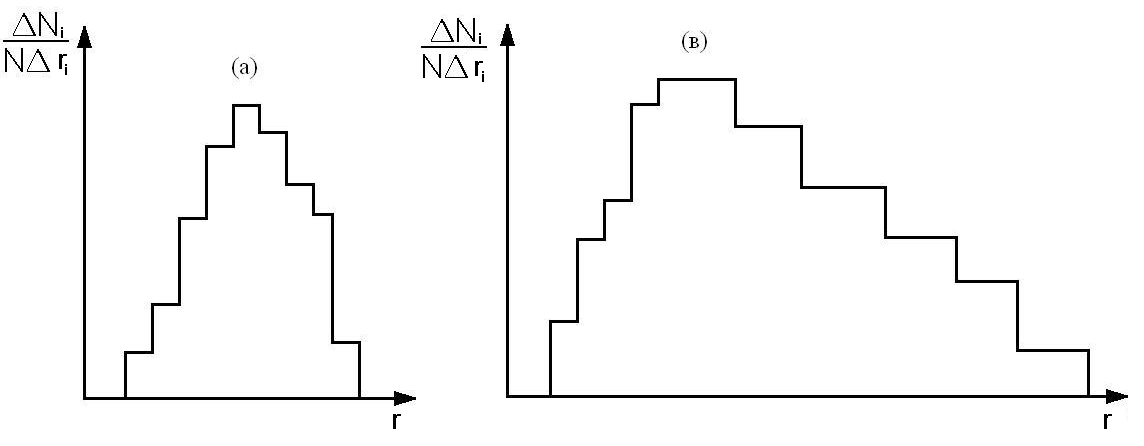
Какие величины отложены по ординатам и абсциссам на гистограммах?

На гистограммах (а) и (в) по осям ординат отложены величины ,

где - количество частиц, размеры которых попадают в интервал [ ),

.

По осям абсцисс отложены величины r.

Обратите внимание, что площади поверхностей под гистограммами равны 1. Действительно, = 1.

Какими двухпараметрическими функциями распределения обычно аппроксимируют эти экспериментальные данные?

(а) – нормальным (симметричным) распределением Гаусса с параметрами распределения < r > и δ_r²

(в) – логарифмически - нормальным распределением Колмогорова с параметрами распределения

< lgr > и δ_lgr² .

Как найти эти параметры, используя экспериментальные данные?

< r > = , , , .

Но лучше использовать построение графиков в вероятностно-логарифмической системе координат (см. домашнее задание).

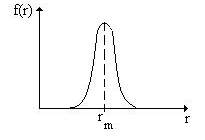
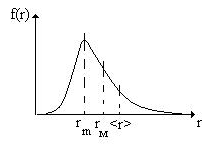
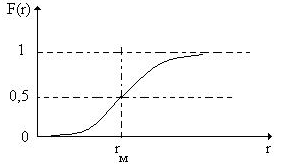
2. Изобразите примерный вид графиков дифференциальной f(r) и интегральной F(r) функций распределения аэрозольных частиц (а.ч.) по размерам r. Изобразите на осях абсцисс этих графиков примерное расположение модального r_m, медианного r_м и среднего < r > размеров а.ч. Каков физичеcкий смысл произведения f(r) · dr и функции F(r)?

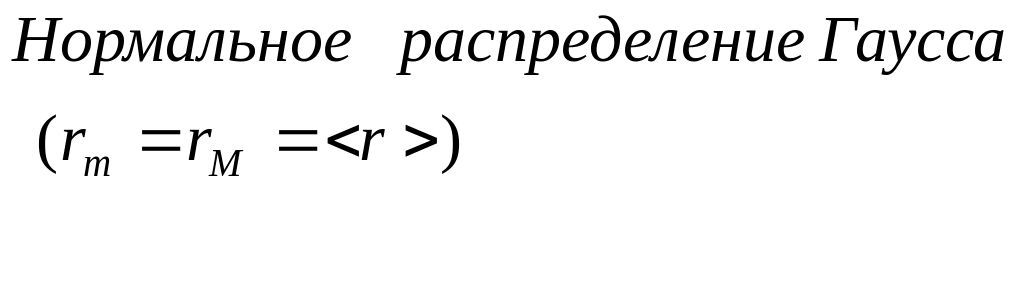
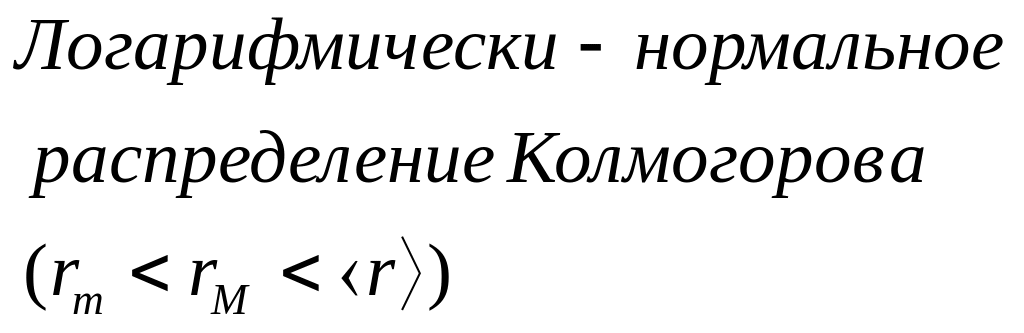
Физический смысл функции f(r) – это плотность вероятности того, что наугад взятая из данной пробы частица имеет размер r.

Физичеcкий смысл произведения f(r) · dr – это вероятность того, что аэрозольная частица, наугад взятая из данной пробы, имеет размер в интервале от r до r + dr.

Физичеcкий смысл функции F(r) – это вероятность того, что наугад взятая из данной пробы аэрозольная частица имеет размер из интервала от 0 до r.

1.1.2. Силы, действующие на аэрозольные частицы. Их использование для очистки газов

3. На аэрозольную частицу могут действовать силы: 1) сила гидродинамического сопротивления среды, 2) сила тяжести, 3) выталкивающая сила Архимеда, 4) сила инерции, возникающая при изменении скорости и направления движения частицы, например, центробежная сила, возникающая при изменении направления движения, 5) кулоновская сила, 6) сила давления света, 7) термофоретическая сила в среде с отличным от нуля градиентом температуры, 8) сила гидродинамического взаимодействия с другими частицами (используйте для объяснения этой силы закон Д.Бернулли или формулу Н.Е.Жуковского о подъемной силе крыла).

4. Частицы дисперсной фазы можно удалять из газа или жидкости, используя силы: 1) тяжести mg в отстойниках или в пылевых камерах, 2) центробежную mu²/R в циклонах, гидроциклонах, импакторах, волокнистых фильтрах, 3) кулоновскую qE в электрофильтрах, в заряженных волокнистых фильтрах.

Примечание. В жидкости частицы могут осаждаться на дно, если сила тяжести больше выталкивающей силы Архимеда, но могут и всплывать, если сила тяжести меньше выталкивающей силы Архимеда. Последний случай относится, например, к всплыванию частиц суспензии нефти в воде (плотность нефти ≈ 0.85 т/м³, плотность воды 1 т/м³).

5. Формула Стокса описывает зависимость силы гидродинамического сопротивления F сплошной (Kn 0) вязкой (μ > 0) среды сферической частице с радиусом r, движущейся относительно газовой или жидкой среды с постоянной скоростью v при условии ламинарного обтекания средой ее поверхности (Re → 0). Формула Стокса получена в результате решения уравнения Навье-Стокса с опущенными инерционными членами. При увеличении критерия Рейнольдса погрешность вычисления силы сопротивления по формуле Стокса увеличивается. При Re  0.1 относительная погрешность вычисления силы трения по формуле Стокса составляет  1,5%. Примерно в четыре раза уменьшается погрешность вычисления, если использовать решение уравнения Навье - Стокса с частичным учетом инерционного члена

(1 + Re)

При вычислении силы сопротивления разреженного по отношению к размеру r частицы газа (Kn > 0) дискретность среды в формуле Стокса учитывается эмпирической поправкой Кенингема С_к.

/ С_к, С_к = 1 + А·Кn + Q ∙Kn · exp(-b·Kn^-1), Kn = < l_r > / r где < l_r > - средний свободный пробег газовых молекул (< l_r > = 6.63∙10^-8 м при н.у.).

Постоянные А, Q и b зависят от материала частиц и от температуры. В частности для масляных капелек (именно с ними экспериментировал Кенингем) при Т = 20^оС А = 1.257, Q = 0.42, b = 0.87.