
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Кузбасский государственный технический университет имени Т.Ф.Горбачева »
Кафедра математики
Е. В. Прейс Е. А. Волкова А. В. Рябкова
Пределы. Дифференциальное исчисление.
Рекомендовано учебно-методической комиссией
специальности 130400.65 «Горное дело» специализация «Горные машины и оборудование» в качестве электронного издания для самостоятельной работы студентов.
КЕМЕРОВО 2011
Рецензенты:
Волков В.М. - доцент кафедры высшей математики,
Хорешок А.А. - председатель учебно-методической комиссии специальности 130400.65 «Горное дело» специализация «Горные машины и оборудование».
Прейс Елена Валерьевна, Волкова Екатерина Анатольевна,
Рябкова Анна Вячеславовна. Пределы. Дифференциальное исчисление: методические указания для самостоятельной работы по математике [электронный ресурс]: для студентов очной формы обучения специальности 130400.65 «Горное дело» специализация «Горные машины и оборудование» / Е. В. Прейс. Е. А. Волкова. А. В. Рябкова. – электрон. дан. – Кемерово: КузТУ , 2011. – 1 электрон. опт. диск (CD-ROM) ; зв. цв. ; 12 см. – Систем. требования : Pentium IV; ОЗУ 8 Мб ; Windows 95 ; (CD - ROM – дисковод) ; Загл. с экрана.
Методические указания предназначены для организации самостоятельной работы студентов по теме «Пределы. Дифференциальное исчисление » и представляют собой решения типовых заданий с подробными пояснениями, а также сами задания для самостоятельной работы. Цель работы – помочь студентам выработать умения и навыки, необходимые при изучении технических дисциплин и освоении инженерной профессии.
Пределы. Дифференциальное исчисление.
(Типовой расчет №3).
Задание
1.
Найти предел:

 .
.
Подставим вместо
x
под знаком предела. Получим неопределенность
вместо
x
под знаком предела. Получим неопределенность
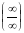 .
Выберем наибольшую степень x
в числителе и знаменателе. В примере
это
.
Выберем наибольшую степень x
в числителе и знаменателе. В примере
это
 .
Поделим числитель и знаменатель на
и найдем значение предела.
.
Поделим числитель и знаменатель на
и найдем значение предела.

Задание
2,3.Найти
пределы.
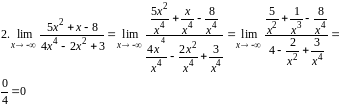 Делим
числитель и знаменатель на
Делим
числитель и знаменатель на
 и
находим предел.
и
находим предел.
3.

(
Делим числитель и знаменатель на
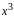 )
)
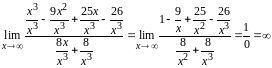
Задание 4,5. Найти пределы.
4.
Подставляем
значение x
=3
под знак предела. Получаем неопределенность
вида
 .
Разложим числитель и знаменатель на
множители, найдя корни квадратных
выражений. Сократим дробь на
.
Разложим числитель и знаменатель на
множители, найдя корни квадратных
выражений. Сократим дробь на
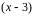 ,
получим
,
получим

5.
Разложим
числитель и знаменатель на множители
и сократим на
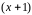 .
Получим
.
Получим
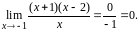
Задание
6.
Найти предел.
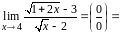
Подставляем x =4 под знак предела, получим
неопределенность
.
Перенесем иррациональность из числителя
в знаменатель. Для этого умножим числитель
и знаменатель на
 .
Аналогично, для переноса иррациональности
из знаменателя в числитель, умножим на
.
Аналогично, для переноса иррациональности
из знаменателя в числитель, умножим на
 ,
получим:
,
получим:

Задание 7,8. Вычислить пределы.
7.

Избавимся от неопределенности в основании, поделив числитель и знаменатель на x.
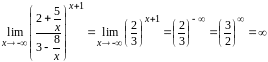
 Неопределенность
Неопределенность
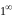 раскрывается
с помощью второго замечательного
предела:
раскрывается
с помощью второго замечательного
предела: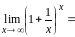 e
e
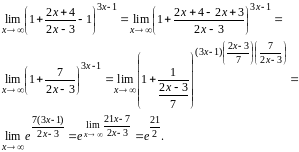
Задание 9,10. Найти пределы, используя первый замечательный предел.
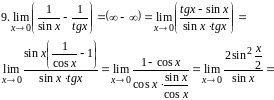
Используя
эквивалентности:
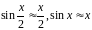 получим
получим
 .
.
10.

Сделаем
замену переменной:
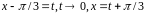 .
.
Воспользуемся формулами:
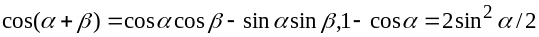 .
.
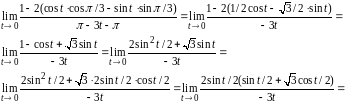
Воспользуемся
эквивалентностью: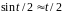 .
Сократим на t.
.
Сократим на t.

Задание 11,12. Исследовать функции на непрерывность.
11.
Исследовать функцию
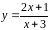 на непрерывность в точках
на непрерывность в точках
 .
Для точки х
= 2 имеем:
.
Для точки х
= 2 имеем:
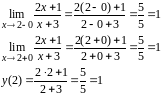 Следовательно, в точке
Следовательно, в точке функция непрерывна, так как правый и
левый пределы равны и равны значению
функции в точке.
функция непрерывна, так как правый и
левый пределы равны и равны значению
функции в точке.
Для
точки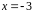 значение функции не существует, правый
и левый пределы равны соответственно:
значение функции не существует, правый
и левый пределы равны соответственно:
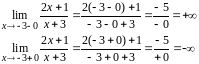 .
.
Следовательно, в точке функция терпит разрыв второго рода.
Задание
12.Исследовать
функцию

Функции
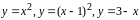 являются непрерывными для любых х.
Следовательно, исходная функция может
иметь разрывы в точках
являются непрерывными для любых х.
Следовательно, исходная функция может
иметь разрывы в точках
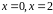 ,
т.е. в точках соприкосновения этих
функций. Проверим это.
,
т.е. в точках соприкосновения этих
функций. Проверим это.
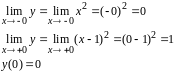
Правый
и левый пределы не равны, следовательно,
функция у
терпит разрыв первого рода в точке
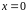 (точка скачка).
(точка скачка).
Для имеем:
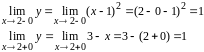
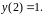 Следовательно,
при
,
функция непрерывна.
Следовательно,
при
,
функция непрерывна.
Задание 13,14,15.Продифференцировать данные функции.
13.
Воспользуемся
правилами дифференцирования
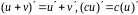 и таблицей производных для сложных
функций, в частности
и таблицей производных для сложных
функций, в частности

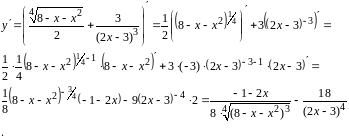

Чтобы
взять производную функции
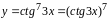 воспользуемся
формулой
воспользуемся
формулой
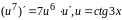 .
.
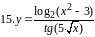
Воспользуемся
правилом дифференцирования
 ,
и таблицей производных для сложных
функций.
,
и таблицей производных для сложных
функций.
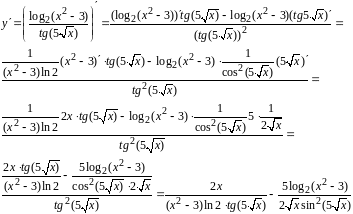
Задание 16,17,18,19. Найти производные функций.
16,17.
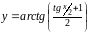 .
.
Воспользуемся формулами дифференцирования сложных функций.
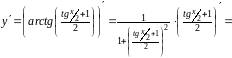
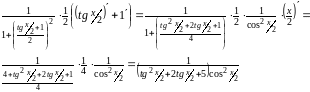 .
.
18,19.


Задание
20.Найти
производную функции
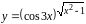 .
.
Применим логарифмическое дифференцирование. Для этого прологарифмируем функцию у.
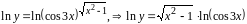 .
.
Дифференцируем обе части равенства, считая у сложной функцией
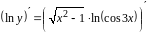
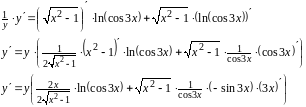
Подставим
вместо у
заданную функцию
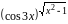 .
.
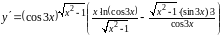
Задание
21.
Найти производную функции заданной в
параметрическом виде в точке
 .
.

Производная
функции
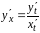 .
Найдем
.
Найдем
 .
.

Задание 22.Найти производную неявно заданной функции.

Дифференцируем
обе части уравнения, считая
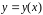 сложной функцией.
сложной функцией.
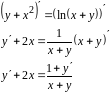
Выразим
 через x
и y.
Для этого перенесем слагаемые с
через x
и y.
Для этого перенесем слагаемые с
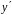 в левую часть, все остальные , в правую.
в левую часть, все остальные , в правую.

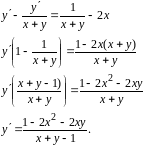
Задание 23.Найти производную III порядка для функции

Найдем первую производную.

Найдем вторую производную. Для этого продифференцируем первую производную еще раз.
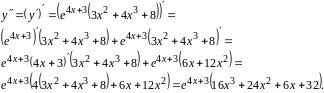
Найдем третью производную.

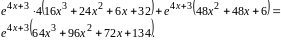
Задание
24.
Показать, что функция
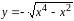 удовлетворяет уравнению
удовлетворяет уравнению
 .
.
Найдем производную функции у , которая входит в уравнение.
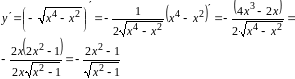
Подставим полученную производную и функцию у в заданное уравнение.
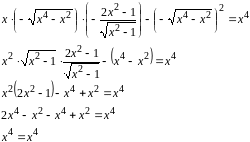
Задание 25.Найти наименьшее и наибольшее значение функции
 на
отрезке
на
отрезке
 .
.
Найдем
критические точки для функции у.
Найдем производную функции и решим
уравнение
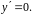
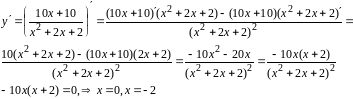
Точка
 .
Найдем значения функции в точках
.
Найдем значения функции в точках .
.

Наибольшее
значение у
=5
функция достигает в точке
.
Наименьшее значение у
=0
функция достигает в точке .
.
Задание 26.Провести исследование функций и построить их графики (функцию а - исследовать с помощью производных).
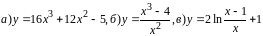

Функция
у
существует при
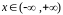 .
Исследуем функцию на экстремумы. Найдем
производную и решим уравнение
.
Исследуем функцию на экстремумы. Найдем
производную и решим уравнение

Разобьем область определения функции этими точками на
и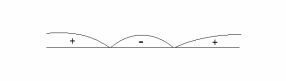 нтервалы.
Определим знак производной и поведение
функции в этих интервалах.
нтервалы.
Определим знак производной и поведение
функции в этих интервалах.
 у
у
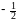 0
0
При
 функция возрастает. При
функция возрастает. При
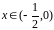 функция убывает. Точка
функция убывает. Точка
 является точкой максимума, так как
производная меняет знак с «плюса» на
«минус» при переходе через эту точку,
является точкой максимума, так как
производная меняет знак с «плюса» на
«минус» при переходе через эту точку,
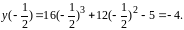 Точка
Точка
является
точкой минимума, так как производная
меняет знак с «минуса» на «плюс» при
переходе через эту точку,

Найдем
точки перегиба функции у.
Найдем
 ,
решим уравнение
,
решим уравнение
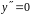 .
.
 .
.
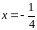 .
.
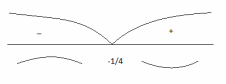
Разобьем
область определения функции точкой
на интервалы. Вторая производная сменила
знак при переходе через эту точку.
Следовательно, это точка перегиба.
Функция у
является выпуклой для
 и вогнутой для
и вогнутой для
 .
.
Найдем
 .
.
Нанесем все найденные точки и построим график функции.
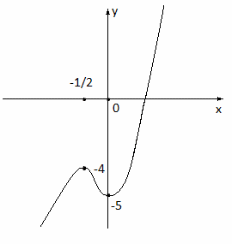
б)
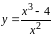 .
.
Областью
определения функции является множество
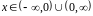 .
В точке
.
В точке
 значение функции не существует.
значение функции не существует.
Найдем
точки пересечения функции с осями
координат. Нули функции дают точки
пересечения с осью ОХ.
 , если
, если
 .
С осью ОУ функция не пересекается.
.
С осью ОУ функция не пересекается.
Проверим
четность
 , нечетность
, нечетность
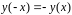 функции у
.
функции у
.
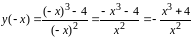 .
.
Условие четности, нечетности не выполняются. Следовательно, функция у общего вида и не является симметричной.
Так как значение функции в точке х=0 не существует, исследуем функцию на разрыв.
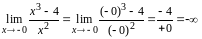
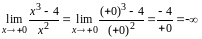
Функция имеет в точке х =0 разрыв II и вертикальную асимптоту.
