
- •Расчет электрических цепей постоянного тока
- •Предисловие.
- •Анализ линейных электрических цепей постоянного тока
- •Проводим анализ схемы
- •2. Изображение всех деревьев графа, выбор одного дерева для дальнейшего расчета схемы
- •Составляем матрицу соединений (узловую
- •4 . Выбираем главные сечения и составляем матрицу главных сечений.
- •5. Записать с помощью матриц [а] и [Дг] две системы уравнений по 1-му закону Кирхгофа:
- •6. Выбрать главные контуры и составить матрицу контуров [в]:
- •8. Записать компонентные уравнения ветвей связи
- •9. С учетом компонентных уравнений записать систему уравнений по первому и второму законам Кирхгофа и определить токи и напряжения в ветвях.
- •10. Составить систему узловых уравнений, определить потенциалы, напряжения на ветвях и токи в ветвях.
- •11. Составить систему контурных уравнений, определить токи в ветвях
- •12. Определить ток i3 в третьей ветви методом эквивалентного генератора
- •14. Построить потенциальную диаграмму для контура, в котором нет источников тока
- •Содержание
12. Определить ток i3 в третьей ветви методом эквивалентного генератора
Важным принципом эквивалентности, широко применяемым при анализе линейных электрических цепей, является принцип эквивалентного генератора (теорема об активном двухполюснике или теорема Гельмгольца – Тевенена).
Он формулируется следующим образом:
любая линейная электрическая цепь, рассматриваемая относительно двух выводов (активный двухполюсник), эквивалентна реальному источнику с ЭДС, равной напряжению между этими выводами при размыкании внешнего участка цепи, подключенного к этим выводам (режим холостого хода), и внутренним сопротивлением, равным входному сопротивлению пассивного двухполюсника, получающегося при равенстве нулю всех ЭДС для источников ЭДС и токов для источников тока рассматриваемого двухполюсника.
П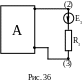 рименим
принцип эквивалентного генератора для
определения тока I3
в третьей ветви нашей электрической
цепи. Для этого выделяем активный
двухполюсник и ветвь с ЭДС E3
и сопротивление R3
рис. 36:
рименим
принцип эквивалентного генератора для
определения тока I3
в третьей ветви нашей электрической
цепи. Для этого выделяем активный
двухполюсник и ветвь с ЭДС E3
и сопротивление R3
рис. 36:
Д алее
можно получить эквивалентную схему,
заменив активный двухполюсник источником
ЭДС – Еэг
– эквивалентного генератора и его
внутреннего сопротивления – Rвнэг.
алее
можно получить эквивалентную схему,
заменив активный двухполюсник источником
ЭДС – Еэг
– эквивалентного генератора и его
внутреннего сопротивления – Rвнэг.
Теперь легко найти ток I3 в простой электрической цепи:
![]() . (107)
. (107)
Чтобы определить
ток I3,
необходимо определить параметры
эквивалентного генератора
![]() и
и
![]() .
.
Таким образом, главное содержание расчета цепи методом эквивалентного генератора состоит в определении эквивалентных параметров и - внутренней части цепи.
В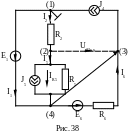 ычисляем
параметры эквивалентного генератора.
Электродвижущая сила эквивалентного
генератора
равна напряжению на выводах внутренней
цепи
ычисляем
параметры эквивалентного генератора.
Электродвижущая сила эквивалентного
генератора
равна напряжению на выводах внутренней
цепи
![]() (режим холостого хода), при отключенной
внешней части (ветви
(режим холостого хода), при отключенной
внешней части (ветви
![]() ,
,
![]() )
(рис. 38).
)
(рис. 38).
Принимаем . (108)
Учитывая, что имеет положительное направление от узла (2) к узлу (3), т.е.
![]() . (109)
. (109)
Э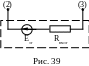 квивалентный
генератор получается, если мы внутреннюю
часть схемы между узлами (2) и (3) заменим
одним источником питания с ЭДС
и сопротивлением
.
квивалентный
генератор получается, если мы внутреннюю
часть схемы между узлами (2) и (3) заменим
одним источником питания с ЭДС
и сопротивлением
.
Учитывая (109), можно записать, что
![]() . (110)
. (110)
Таким образом для
определения
необходимо найти потенциалы
![]() .
Потенциал
найдем с учетом того, что в ветви,
состоящей из Е6,
R6,
протекает ток J4,
как ток идеального источника тока.
.
Потенциал
найдем с учетом того, что в ветви,
состоящей из Е6,
R6,
протекает ток J4,
как ток идеального источника тока.
Следовательно
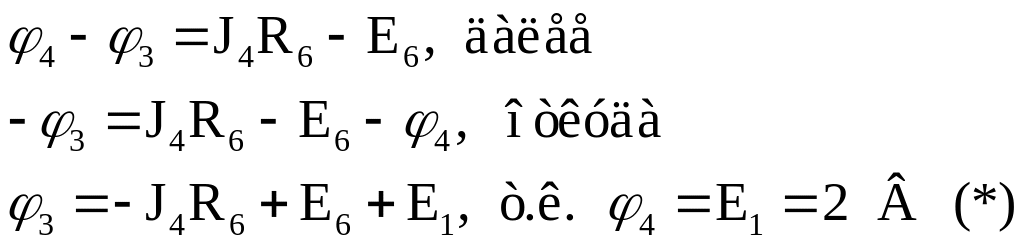
Подставляя значение
![]() в формулу (),
получим:
в формулу (),
получим:
![]() . (111)
. (111)
Теперь определим
потенциал т. (2), по второму закону
Кирхгофа, воспользовавшись тем, что для
контура (1), (2), (4), (1), можно определить
ток I2,
который один и тот же в ветви (1) – (4),
т.е.
![]() .
Потенциал
определяем из уравнения
.
Потенциал
определяем из уравнения
![]() .
Откуда, с учетом
,
имеем
.
Откуда, с учетом
,
имеем
![]() ,
откуда
,
откуда
![]() .
Уравнение для указанного контура,
согласно второму закону Кирхгофа, имеет
вид:
.
Уравнение для указанного контура,
согласно второму закону Кирхгофа, имеет
вид:
![]() .
.
Откуда
![]() ,
следовательно
,
следовательно
![]() . (112)
. (112)
Найдем напряжение :
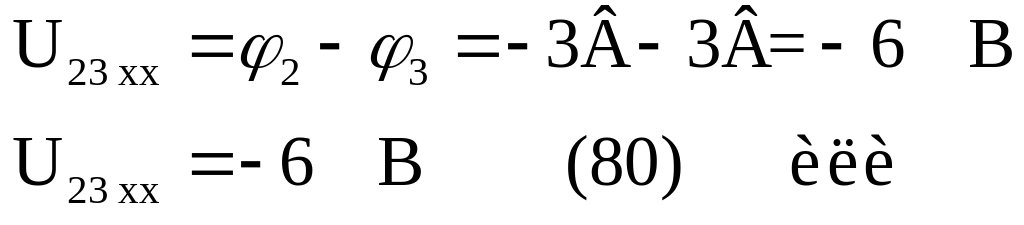
![]() . (113)
. (113)
Определим потенциал второго узла методом узловых потенциалов. Для этого определяем собственную и общую проводимость.
Собственная
проводимость узла (2) равна сумме всех
проводимостей ветвей, примыкающих к
этому узлу. К узлу (2) примыкает ветвь 2
с проводимостью
![]() и ветвь 5 с проводимостью
и ветвь 5 с проводимостью
![]() .
.
Таким образом, собственная проводимость узла (2) в уравнениях записывается со знаком плюс «+» и равна:
![]() . (114)
. (114)
Теперь определяем общую проводимость между узлами (2) и (4). Узел (2) связан с узлом (4) общей проводимостью
![]() . (115)
. (115)
Общая проводимость
в уравнения цепи вносится со знаком
минус «-» -
![]() .
.
Чтобы составить
узловые уравнения для потенциала любого
узла электрической цепи, необходимо
определить собственную проводимость
узла (сумма всех проводимостей ветвей,
примыкающих к узлу цепи), общую проводимость
(проводимость между двумя узлами).
Собственные проводимости узлов
![]() записываются со знаком плюс, а общие
проводимости
записываются со знаком плюс, а общие
проводимости
![]() записываются
со знаком минус. Если ЭДС направлены к
узлу, берутся со знаком плюс, в противном
случае со знаком минус. Также, ток
источника тока берется в уравнении со
знаком плюс, если он направлен к узлу и
с минусом – если он направлен от узла.
записываются
со знаком минус. Если ЭДС направлены к
узлу, берутся со знаком плюс, в противном
случае со знаком минус. Также, ток
источника тока берется в уравнении со
знаком плюс, если он направлен к узлу и
с минусом – если он направлен от узла.
Для составления
уравнения узлового потенциала необходимо
в левой части уравнения взять произведение
потенциала узла на собственную
проводимость
![]() со знаком плюс, произведение потенциала
узла
со знаком плюс, произведение потенциала
узла
![]() ,
который связан с заданным, на общую
проводимость между этими узлами
,
который связан с заданным, на общую
проводимость между этими узлами
![]() со знаком минус. Итак, левая часть
узлового уравнения для узла (2) относительно
узла (4) будет иметь вид:
со знаком минус. Итак, левая часть
узлового уравнения для узла (2) относительно
узла (4) будет иметь вид:
![]() . (116)
. (116)
В правой части берется сумма произведений ЭДС на проводимости ветвей и токов источников тока, при чем, если ЭДС и ток источника тока направлено к узлу, то эти слагаемые берутся со знаком плюс, в противном случае – со знаком минус.
Уравнение правой части для узлового потенциала узла (2) по отношению к узлу (4) будет иметь следующий вид, так как J5 направлен от узла (2) и ЭДС отсутствуют, равно
![]() . (117)
. (117)
Полное уравнение для узла (2) относительно узла (4) будет иметь следующий вид:
![]() . (118)
. (118)
Потенциал узла (4) известен из предыдущего решения:
![]()
Далее подставляем
значения
![]() в уравнение (118):
в уравнение (118):
![]() ,
откуда
,
откуда
![]() ,
следовательно,
,
следовательно,
![]() и, окончательно,
и, окончательно,
![]() . (119)
. (119)
Результат этого
метода чуть завышен, это определяется
точностью, с которой мы определяем
проводимости ветвей. В нашем случае мы
взяли точность определения проводимостей
до второго знака после запятой
![]() .
Если вычислять с точностью до 3, 4, 5
знаков, то результат будет точнее.
.
Если вычислять с точностью до 3, 4, 5
знаков, то результат будет точнее.
Таким образом, точность метода узловых потенциалов зависит от точности определения проводимостей ветвей, чем с большей точностью (до 3-го, 4-го, 5-го значащего числа после запятой) мы определяем проводимости ветвей, тем точнее метод узловых потенциалов.
Определяем
внутреннее сопротивление эквивалентного
генератора
,
которое равно общему сопротивлению
внутренней части цепи
![]() относительно узлов (2) и (3) при равенстве
нулю всех ЭДС для источников ЭДС и токов
для источников тока для рассматриваемого
двухполюсника и отключенной внешней
части цепи (
относительно узлов (2) и (3) при равенстве
нулю всех ЭДС для источников ЭДС и токов
для источников тока для рассматриваемого
двухполюсника и отключенной внешней
части цепи (![]() ).
).
Э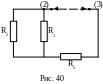 квивалентная
схема двухполюсника для определения
,
приобретает вид:
квивалентная
схема двухполюсника для определения
,
приобретает вид:
Которая получена из схемы (рис. 38).
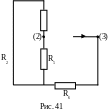
Анализируя схемы
рис. 40, рис. 41, приходим к выводу, что R2
и R5
включены параллельно и к ним последовательно
подключено сопротивление R6.
Общее сопротивление относительно узлов
(2) и (3) будет равно сумме общего
сопротивления параллельно включенных
резисторов R2
и R5
и сопротивления R6,
следовательно
![]() .
.
Подставляем
значение
![]() и
и
![]() в уравнение для
,
получаем:
в уравнение для
,
получаем:
![]()
Таким образом,
выходное сопротивление двухполюсника,
равное внутреннему сопротивлению
равно
![]() .
.
Теперь можно
определить ток в третьей ветви
![]() .
.
Результат совпадает со всеми результатами расчета тока I3 другими методами.
13. Проверяем соблюдение баланса мощности в электрической цепи. Определяем расход энергии за t = 10 с.
Баланс мощностей
Из закона сохранения
энергии следует, что сумма мощностей,
развиваемых источниками электрической
энергии, равна сумме мощностей потребителей
![]() .
.
Причем для источника
ЭДС, направления ЭДС которого совпадает
с направлением тока, то источник ЭДС
доставляет в цепь энергию в единицу
времени (мощность), равную
![]() ,
и произведение EI
входит в уравнение энергетического
баланса с положительным знаком.
,
и произведение EI
входит в уравнение энергетического
баланса с положительным знаком.
Если направление
ЭДС и тока противоположны, то источник
ЭДС не поставляет мощность в цепь (рис.
43), а потребляет ее
![]() ,
и произведение EI
войдет в управление энергетического
баланса с отрицательным знаком.
,
и произведение EI
войдет в управление энергетического
баланса с отрицательным знаком.


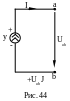

Для источника тока, если направление тока внутри источника J и напряжение между его выводами Uab противоположны (рис. 44).
![]() .
.
Если же направление тока внутри источника J и напряжения между его выводами Uab совпадают по направлению, то (рис. 45):
![]() .
.
Составим баланс мощностей цепи согласно выражению
![]()
![]()
1. Для первой ветви, в которой имеется идеальный источник ЭДС и направление ЭДС Е1 совпадает с током I1, следовательно:
![]() .
.
Во второй ветви источников электрической энергии нет. Ветвь потребляет электрическую энергию:
![]() .
.
3. В третьей ветви имеется источник ЭДС Е3 и сопротивление R3. Так как направление тока I3 встречно направлению ЭДС Е3, то источник ЭДС не поставляет энергию, а потребляет ее и произведение E3 I3 войдет в уравнение энергетического баланса с отрицательным знаком:
![]() .
.
Сопротивление R3 является приемником электрической энергии. Мощность, выделяемая на нем равна:
![]() .
.
4. В четвертой ветви
имеется идеальный источник тока, причем
направление тока J4
и напряжение
![]() по направлению совпадают, следовательно
по направлению совпадают, следовательно
![]() .
.
5. В пятой ветви
также имеется источник тока J5,
направление тока внутри источника тока
J5
и направление напряжения
![]() не совпадают, значит:
не совпадают, значит:
![]() .
.
Сопротивление R5 в этой же цепи является приемником электрической энергии, следовательно,
![]() .
.
6. В шестой ветви имеется источник ЭДС Е6 и сопротивление R6. Источник ЭДС является источником электрической энергии. Направление ЭДС Е6 и направление тока I6 совпадают, следовательно:
![]() .
.
Сопротивление R6
является приемником электрической
энергии. Мощность, потребляемая в нем
равна
![]() .
.
Проанализировав,
каким образом электрическая энергия
источников электрической энергии
перераспределяется в ветвях электрической
цепи составим в соответствии с выражением
![]() ;
уравнение баланса мощностей:
;
уравнение баланса мощностей:
![]()
Подставляем в уравнение баланса мощностей значения всех величин, полученных при решении электрической цепи:
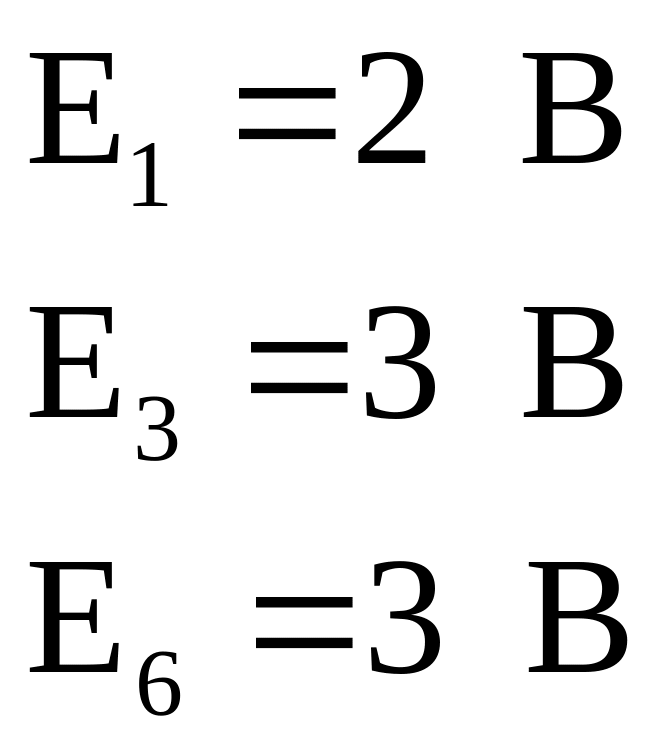
![]()
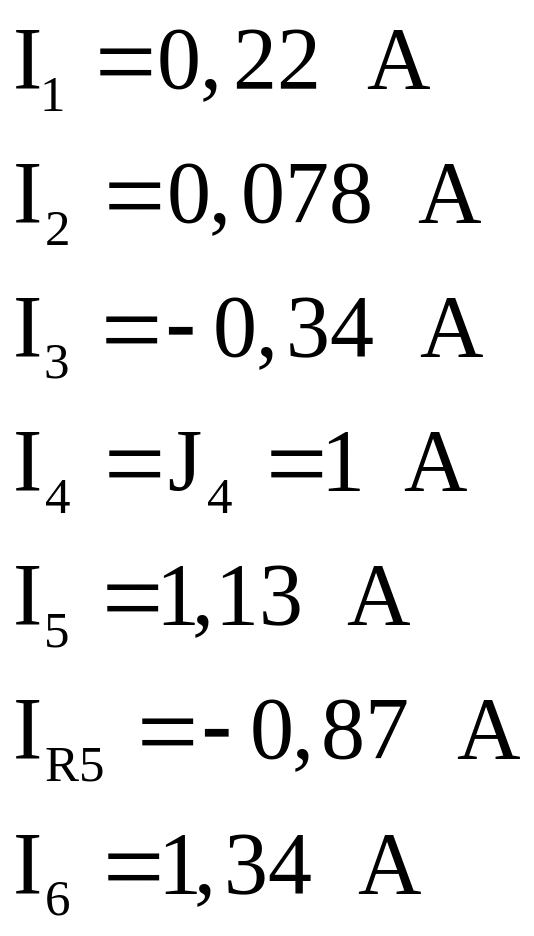
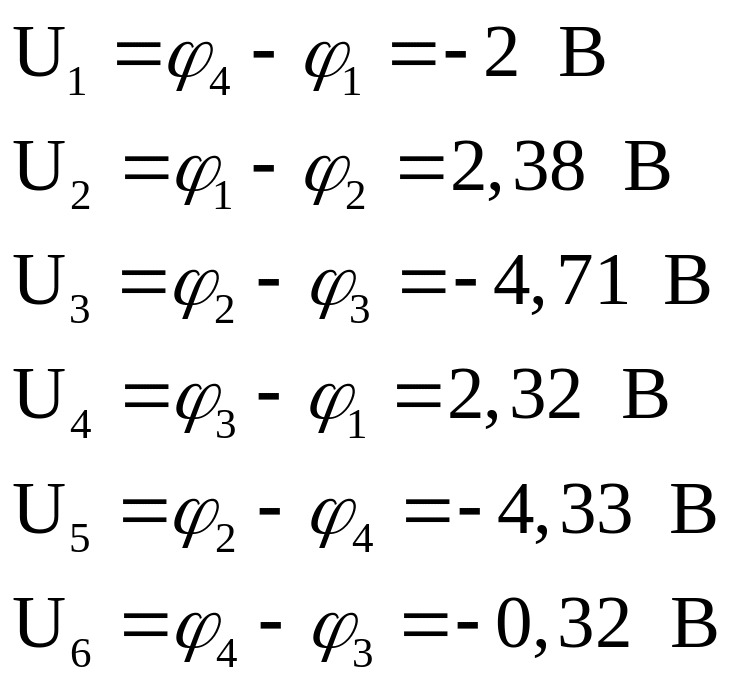
получим:
![]()
![]() .
Далее
.
Далее
![]()
![]() и окончательно:
и окончательно:
![]()
Таким образом, мы убедились, что при верном решении баланс мощностей цепи выполняется.
В этой связи делаем вывод, что наиболее полной (исчерпывающей) проверкой правильности расчета электрической цепи является выполнения условия баланса мощностей. Поэтому полезно составлять баланс мощностей даже в тех случаях, когда по условию задачи его можно и не составлять.
Определяем расход
энергии за 10с.: если для поддержания
тока I
в каком-либо участке электрической цепи
требуется иметь на зажимах участка
напряжение U,
то работа электрического тока на этом
участке за время t
может быть выражена формулой
![]() ,
а соответствующая мощность
,
а соответствующая мощность
![]() .
.
Если напряжение в этих формулах выражено в вольтах, ток – к амперах, а время – в секундах, то мощность измеряется в ваттах (Вт), а работа в джоулях (Дж) или ватт - секундах (1 ватт - секунда = 1 вольт – ампер – секунда = 1 джоуль).
Если же время выражать не в секундах, а в часах (ч), то работа получается в более крупных единицах – ватт – часах (Вт ч). Значит 1 Вт ч = 3600 Дж.
Энергия, расходуемая за t = 10 с в электрической цепи при мощности источников 9,78 Вт равна:
![]()
