- •§1. Предмет і методи аналітичної геометрії
- •§2. Системи координат Декартова система координат
- •Полярна система координат
- •Перетворення системи координат
- •Паралельний зсув осей
- •Поворот осей координат
- •§3. Основні та найпростіші задачі аналітичної геометрії Основні задачі аналітичної геометрії
- •Найпростіші задачі аналітичної геометрії
- •§4. Пряма лінія на площині
- •Рiвняння прямої, що проходить через задану точку паралельно заданому вектору
- •Параметричне рiвняння прямої
- •Рiвняння прямої, що проходить через задану точку
- •Рiвняння прямої з кутовим коефцiєнтом
- •Рiвняння прямої, що проходить через двi заданi точки
- •Рівняння прямої у відрізках на осях
- •Рiвняння прямої, що проходить через задану точку перпендикулярно до заданого вектора
- •Нормальне рівняння прямої
- •Загальне рівняння прямої
- •Кут між двома прямими
- •Відстань від точки до прямої
- •Контрольні запитання
- •§5. Криві другого порядку. Їхня форма I канонічні рівняння
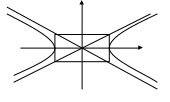
- •Гiпербола
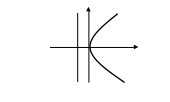
- •Парабола
- •§6. Дослідження загального рівняння кривих другого порядку
- •Навчальні завдання
- •Контрольні запитання
- •Основні формули аналітичної геометрії
Навчальні завдання
1. Пряму задано рівнянням 3х – 5у + 15 = 0. Перевірити, які з точок А (– 2, 3), В (0, 3), С (5, 6), належать заданій прямій, знайти її рівняння з кутовим коефіцієнтом і у відрізках на осях.
Для перевірки того, чи лежать точки А, В, С на прямій, підставимо їхні координати в рівняння прямої:
А: 3 (– 2) – 5 · 3 + 15 0, В: 3 · 0 – 3 · 5 + 15 = 0, С: 3 · 5 – 5 · 6 + 15 = 0.
Таким чином, точка А не лежить на прямій, а точки В і С лежать на прямій.
Поділимо
рівняння прямої почленно на коефіцієнт
при у:
![]() ,
а далі запишемо його у вигляді
,
а далі запишемо його у вигляді
![]() — рівняння з кутовим коефіцієнтом.
— рівняння з кутовим коефіцієнтом.
Поділивши рівняння почленно на вільний член:
![]() ,
,
![]()
шукане рівняння у відрізках на осях.
2. Записати рівняння гіперболи, яка проходить через точку А (6; 9), якщо:
1) відстань між фокусами дорівнює 8, а відстань між директрисами — 6;
2) директриси задано
рівняннями
![]() ,
а кут між асимптотами — прямий;
,
а кут між асимптотами — прямий;
3) ексцентриситет дорівнює = 2, а уявна піввісь b = 3;
4) асимптоти задано
рівнянням
![]() .
.
1) Координати
фокусів F1
(– c;
0); F2
(c;
0), тому з умови
2с
= 8; с
= 4, відстань між директрисами
![]() .
Звідки, враховуючи, що
.
Звідки, враховуючи, що
![]() маємо: а
= 12, b
= c
– a
= 4. Остаточно
маємо: а
= 12, b
= c
– a
= 4. Остаточно
![]() .
.
2) З рівнянь
директрис маємо:
![]() ,
якщо кут між асимптотами прямий, то а
= b.
Отже, з урахуванням формули
,
якщо кут між асимптотами прямий, то а
= b.
Отже, з урахуванням формули
![]() маємо
маємо
![]() і а
= 6; b
= 6. Остаточно записуємо рівняння шуканої
гіперболи:
і а
= 6; b
= 6. Остаточно записуємо рівняння шуканої
гіперболи:
![]() .
.
3) З формули,
застосованої вище, дістаємо
![]() звідки
звідки
![]() .
Отже,
.
Отже,
![]() .
.
4) Точка А
належить гіперболі, тому маємо:
![]() .
З рівняння асимптот гіперболи випливає
співвідношення
.
З рівняння асимптот гіперболи випливає
співвідношення
![]() ,
або
,
або
![]() .
Підставивши b
в останнє співвідношення, дістанемо
рівняння для знаходження а2:
.
Підставивши b
в останнє співвідношення, дістанемо
рівняння для знаходження а2:
![]()
Отже,
![]()
Контрольні запитання
Загальне рівняння кривої другої порядку.
Рівняння кола з центром в точці С(a:b) і радіусом R, побудова.
Рівняння кола з центром в точці С(0;0) і радіусом R, зробити рисунок
Коло.
Еліпс.
Гіпербола.
Парабола.
Ексцентриситет кривих другого порядку.
Розміщення параболи на координатній площині в залежності від значення параметра р.
Асимптоти гіперболи.
Основні формули аналітичної геометрії
Таблиця 3. Пряма на площині
|
Вигляд рівняння прямої |
Назва рівняння |
Пояснення |
1. |
|
Рівняння
прямої, що проходить через точку
|
|
2. |
|
Загальне рівняння |
|
3. |
|
Рівняння прямої з кутовим коефіцієнтом |
кутовий
коефіцієнт,
точка
|
4. |
|
Рівняння прямої, що має кутовий коефіцієнт та проходить через задану точку |
|
5. |
|
Канонічне рівняння прямої |
|
6. |
|
Параметричні рівняння прямої |
|
7. |
|
Рівняння прямої у відрізках |
Точки
|
8. |
|
Рівняння прямої, що проходить через дві точки |
|
9. |
|
Нормальне рівняння прямої |
|
Відстань
від точки
|
|||
|
|
||
|
|
||
Кут
між прямими
|
||
|
|
|
|
|
|
Паралельність та перпендикулярність прямих та на площині |
||
|
║ |
|
|
|
|
|
|
.
|
|
|
|
Таблиця 4. Криві другого порядку
|
Назва, рівняння |
Графік |
1 |
Еліпс
При
|
O a x
y
x |
2 |
Гіпербола
|
y
b
O a x |
3 |
Парабола
|
y d M r
O x |
Таблиця 5. Деякі криві в полярній системі координат
1. |
Кардіоїда
|
|
2. |
Лемніската Бернуллі
|
|
3. |
Завиток Паскаля
|
|
4. |
Трипелюсткова троянда
|
|
5. |
Чотирипелюсткова троянда
|
|
6. |
Спіраль Архімеда
|
|
7. |
Гіперболічна спіраль
|
|
8.
|
Логарифмічна спіраль
|
|
9. |
Жезл
|
|

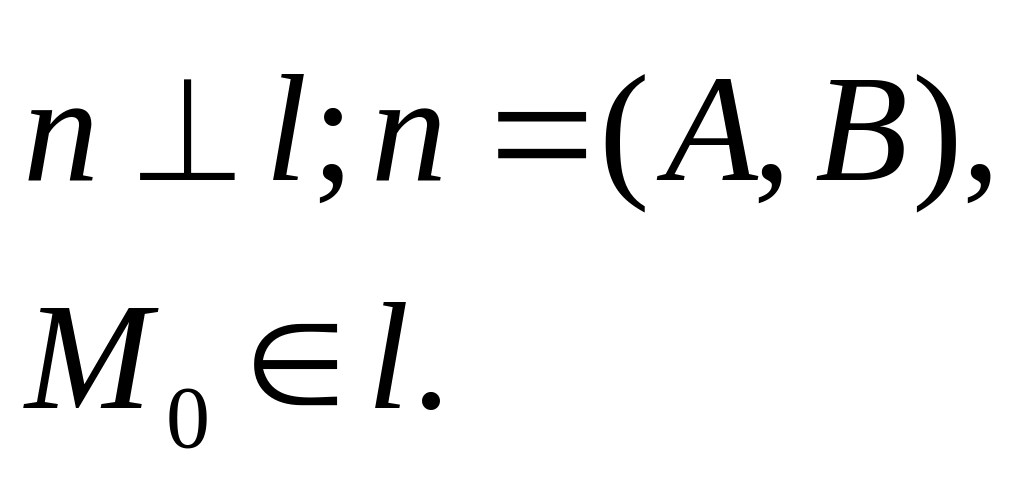
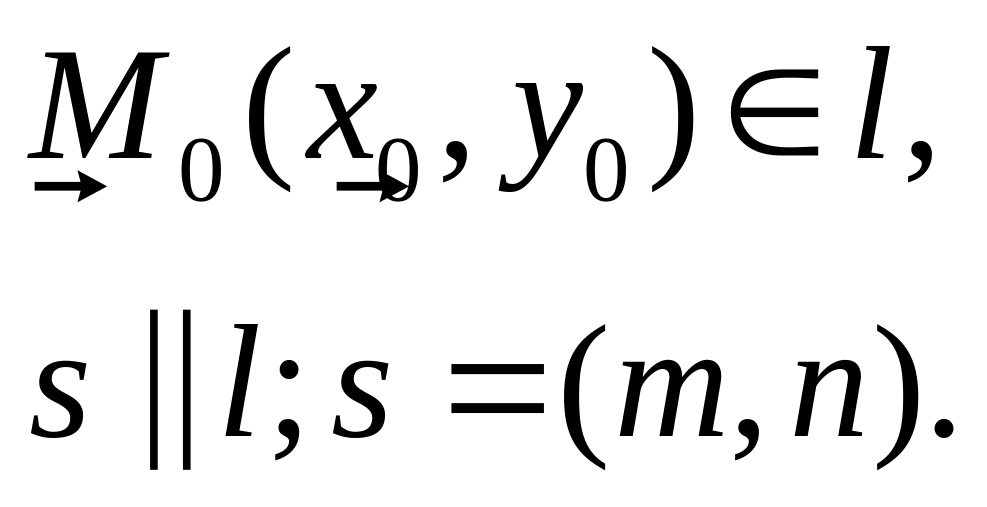

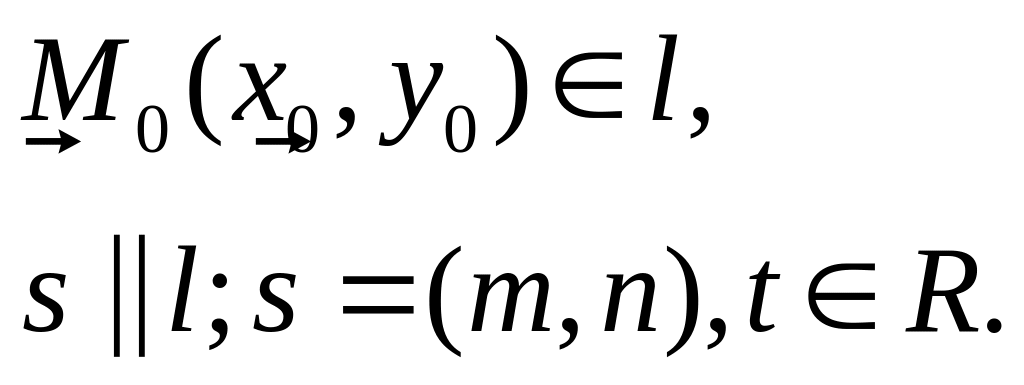
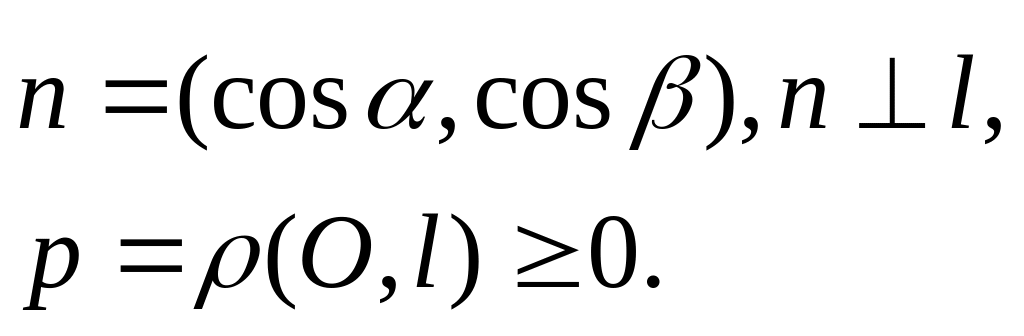
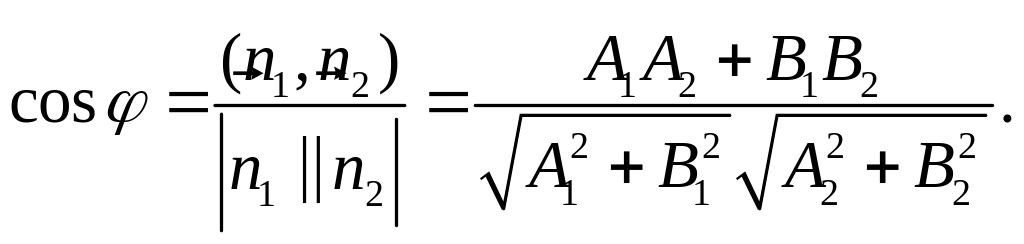
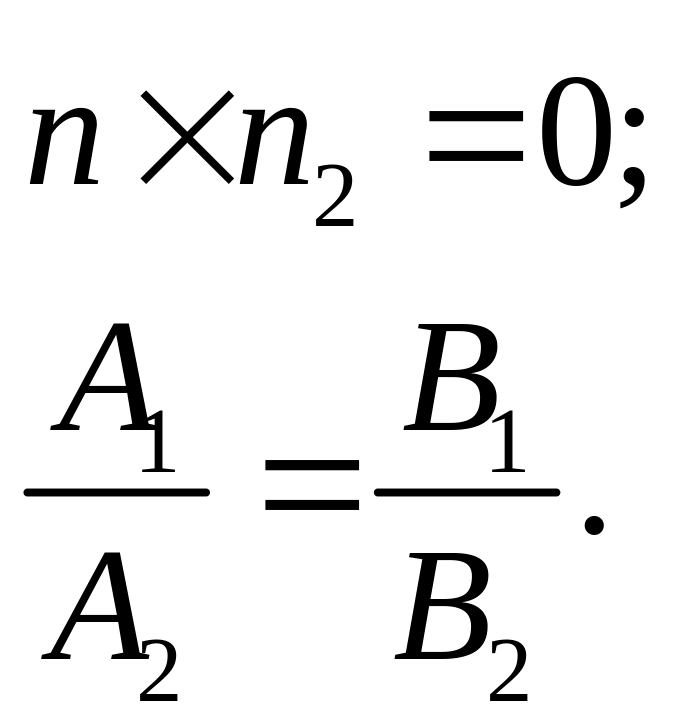
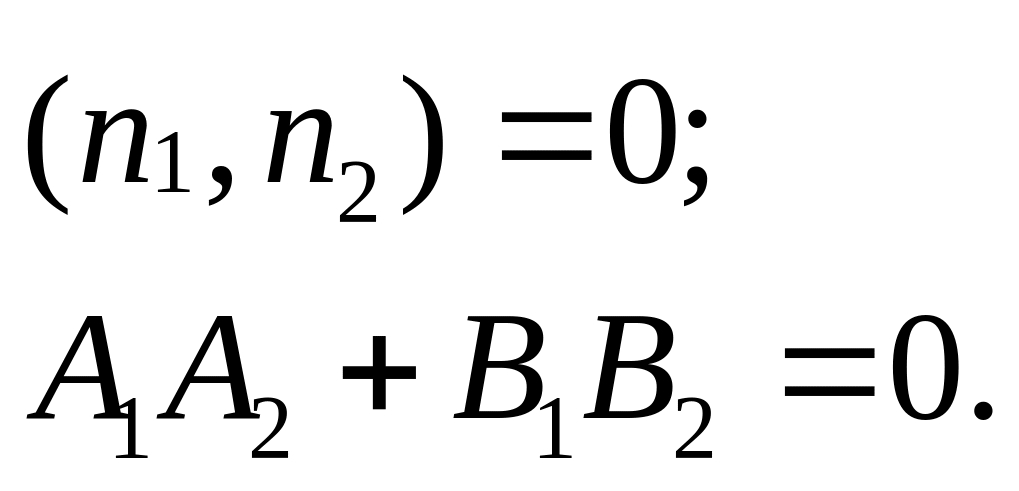
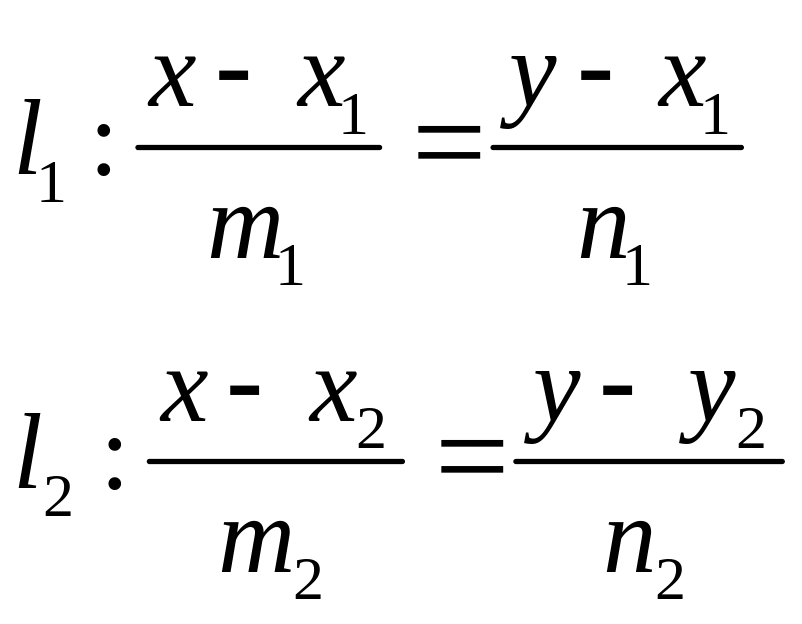
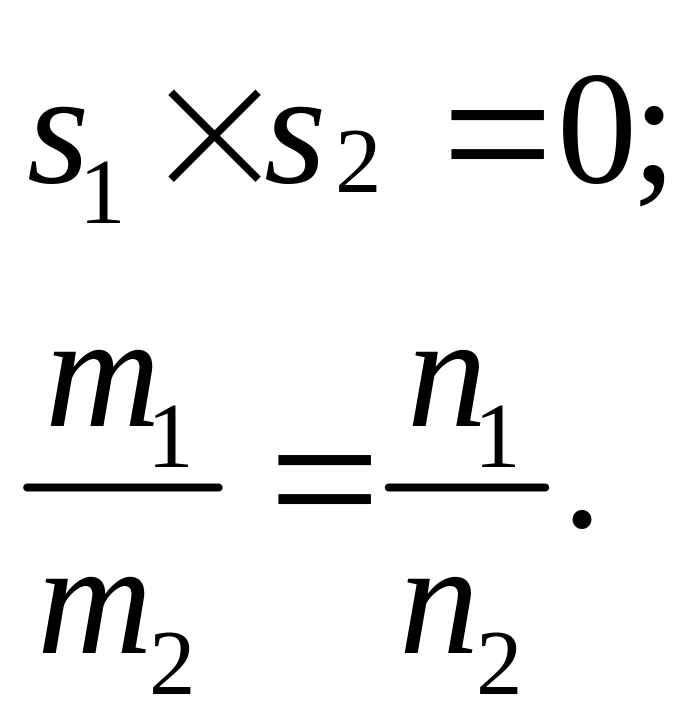
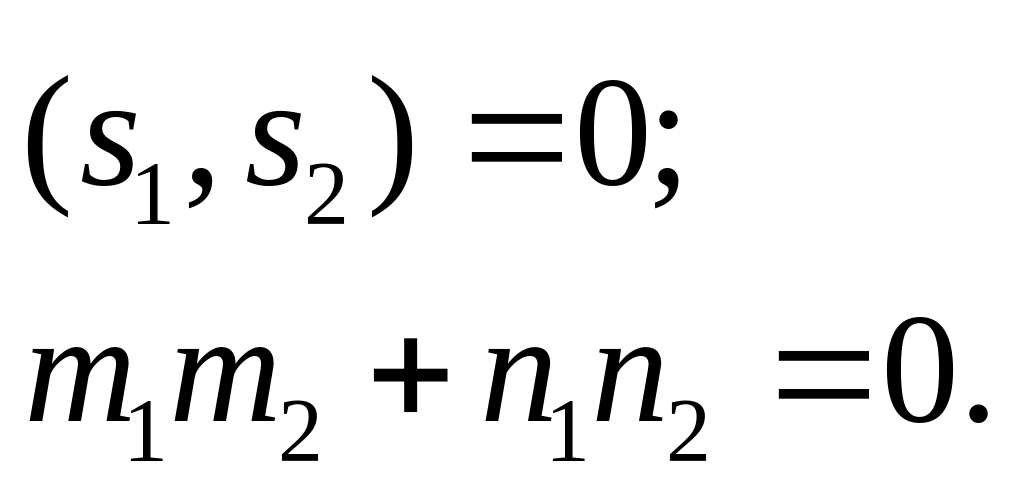
 y
y b
b