Гiпербола

Означення. Гіперболою називають геометричне місце точок площини, для яких модуль різниці відстаней до двох заданих точок (фокусів) є величиною сталою й меншою, ніж відстань між фокусами.

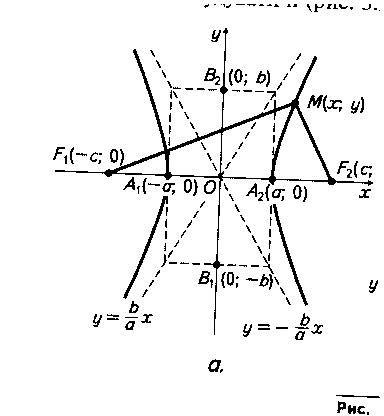
Рис. 18

Канонічне рівняння гіперболи, фокуси якої лежать на осі Ox має вигляд

, (5.8)

де

b² = c² – a². (5.9)

Точки — вершини гіперболи. Точки F₁ (– c, 0) і F₂ (c, 0) — фокуси гіперболи. Відрізки .

Прямі називають асимптотами гіперболи.

Якщо фокуси гіперболи лежать на вісі Оy (рис. 19), то її рівняння має вигляд

(5.10)

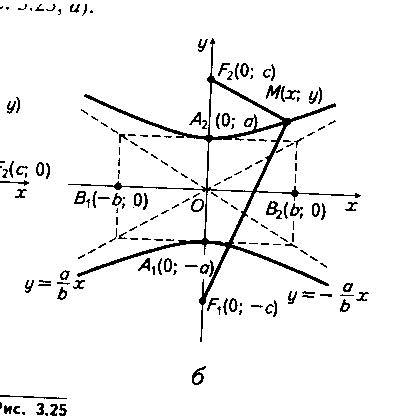
Рис. 19

Означення. Ексцентриситетом гіперболи називають величину

. (5.11)

У гіперболи . Ексцентриситет гіперболи характеризує її форму.

Означення. Якщо дійсна і уявна осі гіперболи рівні, то гіперболу називають рівносторонньою.

Дослідимо рівняння гiперболи. Гіпербола не перетинає вісь Оу. При у = 0; х = а, точки (–а, 0); (а, 0) — точки перетину з віссю Ох.

Прямi, piвняння яких

, (5.12)

називатимемо асимптотами гіперболи.

Відрізки завдовжки b і а називають відповідно уявною і дійсною осями гіперболи.

Ексцентриситет гіперболи , але с > a і е >1. Беручи до уваги, що с² = а² + b², дістаємо: , або .

З останньої рівності випливає, що для гіперболи ексцентриситет характеризує ступінь нахилу віток гіперболи до осі Ох.

Означення. Дві прямі, рівняння яких , називаються директрисами еліпса і гіперболи.

Для еліпса і відношення , директриси еліпса — це дві прямі, що розміщені симетрично відносно осі Оу і проходять зовні еліпса. Для гіперболи  > 1 і відношення . Тобто директриси гіперболи розміщені симетрично відносно осі Оу і лежать між вітками гіперболи.

Для еліпса і гіперболи можна сформулювати наступне важливе твердження.

Якщо r — відстань від деякої точки еліпса або гіперболи до будь-якого фокуса, а d — відстань від цієї самої точки до директриси, яка відповідає цьому фокусу, то відношення стале й дорівнює ексцентриситету: .

Розглянуте твердження можна покласти в основу означення цих ліній.

Означення. Множина точок, для яких відношення відстаней від фокуса і до відповідної директриси — величина стала, що дорівнює ексцентриситету е, є еліпс, якщо е < 1, і гіпербола, якщо е > 1.

Парабола

Означення. Параболою називають геометричне місце точок площини, відстані від яких до заданої точки (фокуса) й заданої прямої (директриси) рівні.

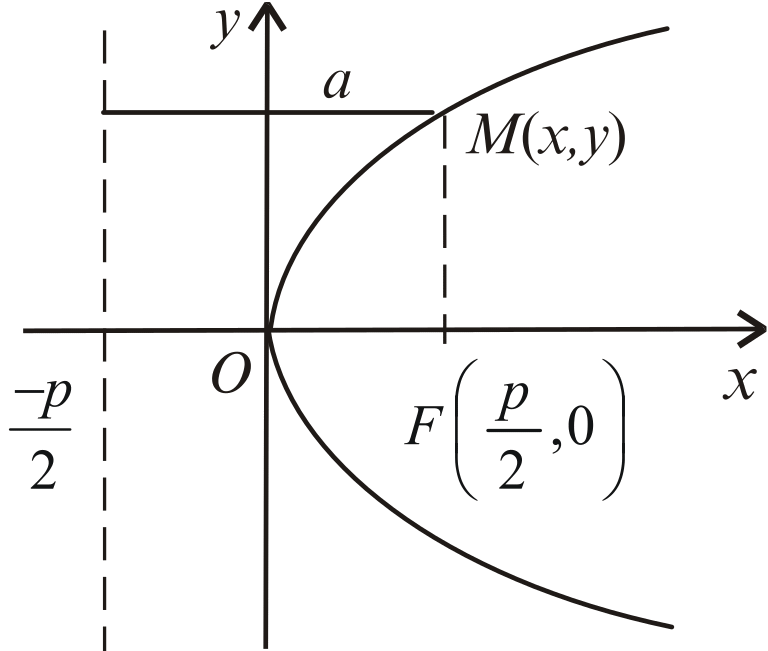
Рис. 20

За означенням r = d, отже (див. рис. 20):

або

у² = 2рх (5.13)

(5.13) — канонічне рівняння параболи. Ексцентриситет параболи е = 1. Парабола симетрична осі Ох, проходить через початок системи координат. Її графік подано на рис. 20. Точка — фокус параболи, пряма — директриса.

Можливі різні розміщення параболи на координатній площині.

§6. Дослідження загального рівняння кривих другого порядку

Загальне рiвняння другого степеня ( з двома змiнними) має вигляд

. (6.1)

Залежно вiд значень коефiцiєнтiв рiвняння (6.1) може визначати коло, елiпс, гiперболу, параболу, пару прямих, якi перетинаються, пару паралельних прямих, пару прямих, якi збiгаються, точку, або не визначати нiякої лінії.

Щоб визначити, яку лінію визначає рiвняння, введемо два визначника

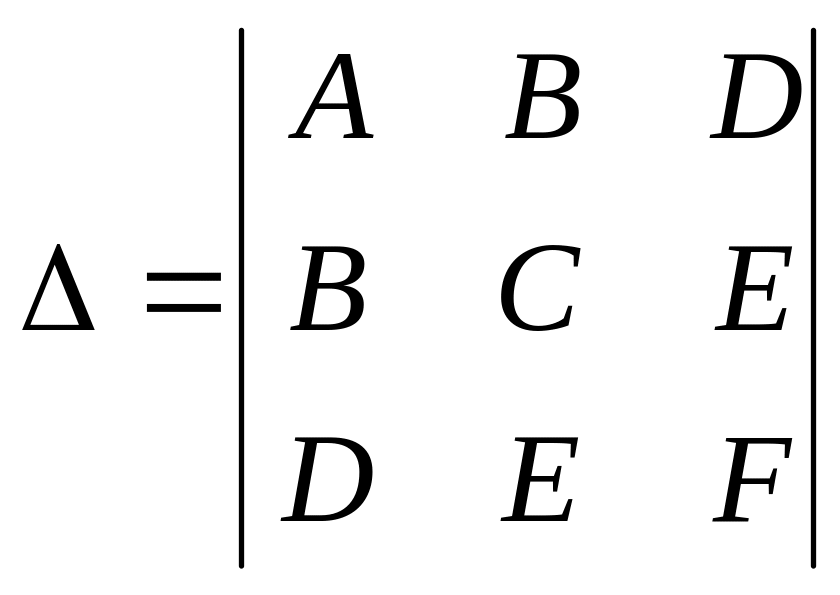, (6.2)

Залежно вiд значень визначникiв (6.2) piвняння (6.1) визначає певний геометричний образ.

Залежнiсть
	Еліпс (дійсний або уявний)	Точка
	Парабола	Паралельні прямі (дійсні, уявні або такі, що збігаються)
	Гіпербола	Дійсні прямі, що перетинаються

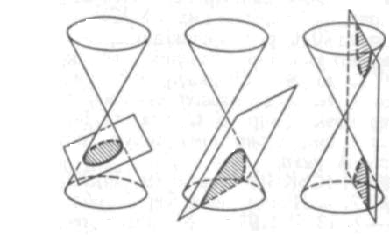
Зауваження. Більшість типів ліній другого порядку відомі давно, їх досить добре вивчив Аполлоній. Він утворював основні типи ліній другого порядку як плоскі перерізи кругового конуса, тому в математичній літературі лінії другого порядку відомі ще як конічні перерізи. Конічні перерізи — невироджені криві, утворені перетином площини з однією або обома частинами конуса. Перетин площини, перпендикулярній осі конуса, утворює коло. Перетин площини, не перпендикулярній осі конуса, з однією з частин конуса утворює еліпс або параболу. Крива, отримана перетином площини з обома частинами конуса називається гіперболою. Також існують вироджені перетини: точка, пряма та пара прямих.

Конічні перерізи: а — еліпс,б — парабола,в — гіпербола.

а б в