Загальне рівняння прямої

З виведених вище рівнянь прямої лінії можна зробити висновок, що всі ці рівняння є рівняннями першого степеня відносно і , тобто лінійними рівняннями. Отже, пряма лінія має своїм рівнянням рівняння першого степеня відносно і .Чи буде правильним обернене твердження? Чи кожне рівняння першого степеня відносно і буде рівнянням прямої? Щоб відповісти на це запитання, доведемо таку теорему.

Теорема. Кожне лінійне рівняння з двома змінними і визначає на площині в декартовій системі координат пряму лінію.

Доведення. Нехай задано лінійне рівняння з двома змінними і :

(4.10)

Припустимо, що це рівняння деякої лінії . Доведемо, що є пряма лінія, тобто що рівняння (4.10) є рівнянням прямої.

Візьмемо на лінії довільну точку Оскільки ця точка належить лінії , то її координати задовольняють рівняння (4.10)

(4.11)

Віднімемо почленно від рівняння (11) рівність (12). Дістанемо:

(4.12)

Рівняння (4.12) еквівалентне рівнянню (4.10) і визначає пряму, що проходить через точку перпендикулярно до вектора Отже, рівняння (4.10) визначає пряму. Це рівняння називають загальним рівнянням прямої. Коефіцієнти А і В загального рівняння прямо є координатами її нормального вектора.

Розглянемо окремі випадки загального рівняння прямої, коли рівняння є неповним (якісь члени рівняння відсутні).

1.У рівнянні прямої немає вільного члена, тобто У цьому разі пряма проходить через початок координат. Справді, точка задовольняє рівняння

2. У рівнянні прямої немає члена, що містить , тобто Тоді пряма паралельна осі , оскільки нормальний вектор цієї прямої перпендикулярний до осі , а пряма, перпендикулярна до нього, паралельна осі .

3. У рівнянні прямої немає члена, що містить , тобто Аналогічно попередньому, пряма паралельна осі

4. У рівнянні прямої немає члена, що містить і вільного члена, тобто Згідно з попереднім, пряма паралельно осі і проходить через початок координат. Отже, рівняння є рівнянням осі

5. У рівнянні прямої немає члена, що містить і вільного члена, тобто Аналогічно попередньому, рівняння є рівнянням осі

Коефіцієнти і одночасно не можуть дорівнювати нулю, бо тоді рівняння першого степеня відносно і не існуватиме.

Кут між двома прямими

Означення. Кутом між прямим l₁ і l₂ називається такий кут , поворот на який від першої прямої до другої відносно точки їх перетину до суміщення цих прямих відбувається на найменший кут проти руху годинникової стрілки.

Кут між двома прямими може вимірюватися кутом між напрямними векторами прямих.

Нехай прямі і задано відповідно канонічними рівняннями

і .

Напрямним вектором прямої є вектор , а прямої — вектор , причому:

Тоді

,

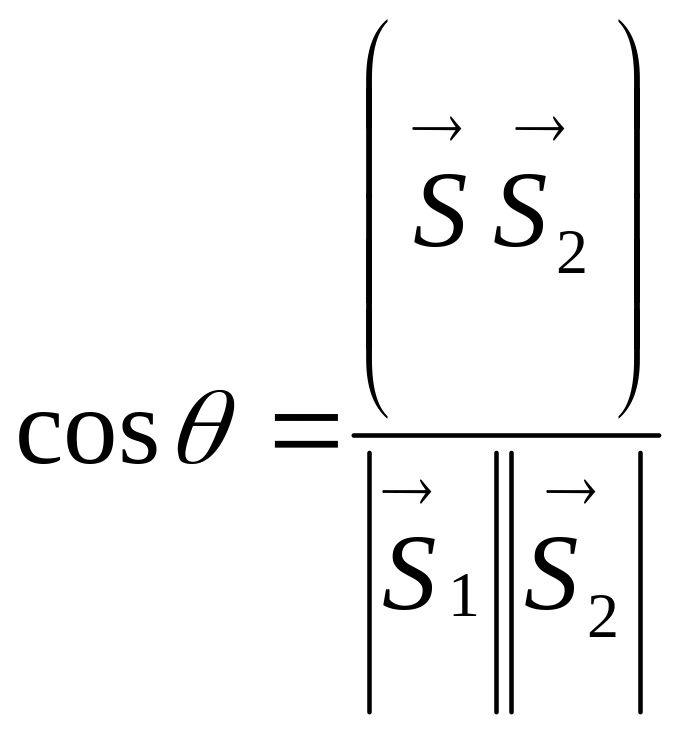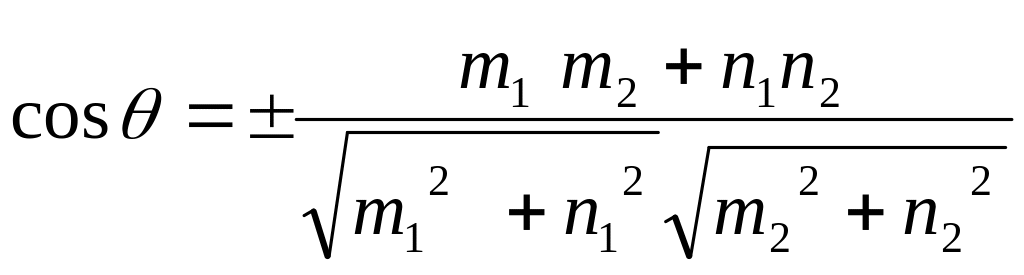(4.13)

0

0

Рис. 14

Знаки «плюс» або «мінус» дають змогу визначити кожен із суміжних кутів, утворених в результаті перетину прямих.

Якщо прямі s паралельні, то вектори і паралельні. Отже, їхні координати пропорційні

(4.14)

(4.14) — умова паралельності двох прямих.

Якщо прямі і перпендикулярні, то їхні напрямні вектори перпендикулярні. Отже, їхній скалярний добуток дорівнює нулю

або

. (4.15)

(4.15) — умова перпендикулярності двох прямих.

Кут між двома прямими може вимірюватися кутом між їхніми нормальними векторами. Нехай прямі і задано відповідно загальними рівняннями:

і

Нормальним вектором прямої буде вектор , а прямої — вектор Кут між векторами і дорівнює одному з кутів між прямими і

Тоді

,

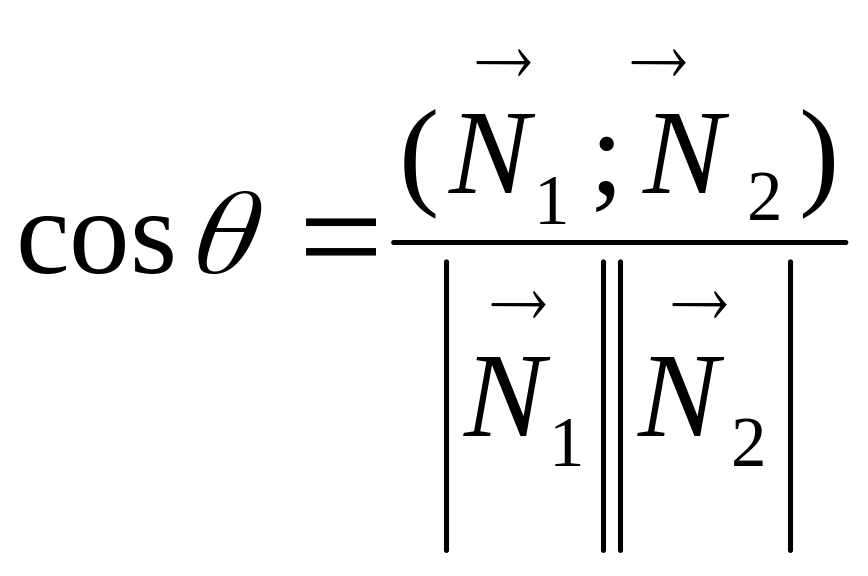або

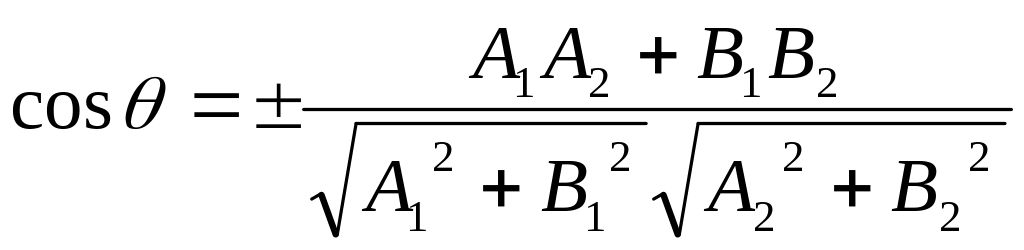(4.16)

(4.16) — формула для обчислення кута між прямими. Знаки «плюс» або «мінус» дають змогу визначити кожен із суміжних кутів, утворених в результаті перетину прямих.

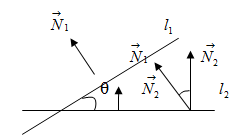
Р ис. 15

Якщо прямі і паралельні, то їх нормальні вектори і паралельні, отже, їхні координати пропорційні

(4.17)

Якщо прямі і взаємно перпендикулярні, то

. (4.18)

(4.18) — умова перпендикулярності двох прямих.

Пропонуємо читачеві довести це самостійно.

Якщо прямі і задано рівняннями з кутовими коефіцієнтами, причому прямі не паралельні осі то кут між ними можна визначити за формулою

, (4.19)

де — кутові коефіцієнти цих прямих.

Справді, нехай задано дві прямі і , не паралельні осі ,

Позначимо кут нахилу до осі через , а кут нахилу до осі через . Як відомо, , а ; через позначимо кут між прямими і , тобто = Прямі і разом з віссю утворюють трикутник, в якого зовнішній кут, який дорівнює сумі внутрішніх кутів, з ним не суміжних. Отже,

Звідки а

але

,

тоді

Якщо прямі і паралельні, то , отже, або

. (4.20)

(4.20) — умова паралельності двох прямих.

Якщо прямі і перпендикулярні, то не існує. Дріб (4.19) не існує, коли або

. (4.21)

(4.21) — умова перпендикулярності двох прямих.