Перетворення системи координат

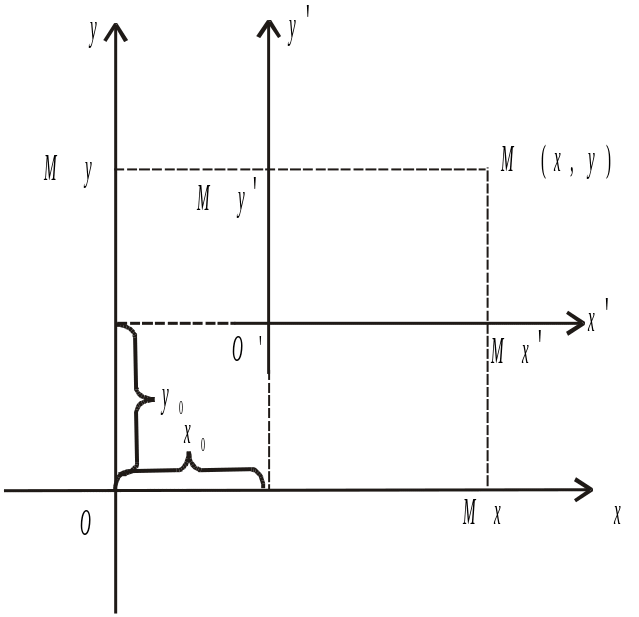
Рис. 4

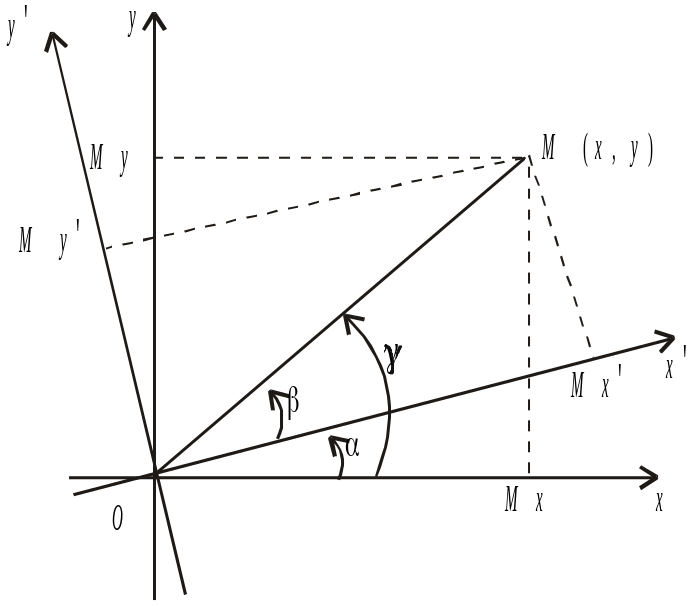
Рис. 5

Паралельний зсув осей

Паралельний зсув осей — перетворення, при якому змінюється положення початку системи координат, а напрям осей залишається без змін (рис.4).

Нехай точка М у старій системі координат Оху має координати (х, у), а в новій системі координат — . Знайдемо зв’язок між координатами точки. З рис.4 бачимо, що

, (2.2)

де (х₀, у₀) — декартові координати початку нової системи координат (точка О´) у старій системі координат. Розв’язуючи рівняння (2.2) відносно і , маємо

.

Поворот осей координат

Поворот осей координат — перетворення, при якому обидві осі повертаються на деякий кут відносно нерухомого початку системи координат (рис.5).

Повернемо тепер стару систему координат Оху відносно точки О на кут  і дістанемо нову систему Охy (рис.5).

Розглянемо дві полярні системи координат з полюсом у точці О і полярними осями Ох і Ох. Тоді згідно з рис.6 маємо

.

Крім того,  =  + , підставляючи це значення  у формули, остаточно будемо мати:

(2.3)

Розв’язуючи рівності (2.3) відносно дістаємо:

= х cos + y sin, = – х sin + y cos. (2.4)

Здобуті формули (2.4) встановлюють зв’язок між старими (x, y) і новими координатами точки.

§3. Основні та найпростіші задачі аналітичної геометрії Основні задачі аналітичної геометрії

1. Cкладання рівняння геометричного об’єкта, який розглядають, як геометричне місце точок.

2. Дослідження властивостей геометричного об’єкта за його рівнянням і його побудова.

Означення. Геометричним мiсцем точок (ГМТ) називають множину точок, якi мають будь–яку загальну для них геометричну властивiсть, при цьому точки, якi не належать цiй множинi, такої властивостi не мають.

Найпростіші задачі аналітичної геометрії

1. Знаходження відстані між двома точками.

Нехай дано дві точки .

Рис. 6

Довжину відрізка визначимо, як довжину вектора :

= (3.1)

2. Ділення відрізка у заданому відношенні.

Нехай необхідно знайти координати точки М, яка ділить відрізок у відношенні .

0

Рис. 7

Означення. Число  — називається відношенням, в якому точка М ділить відрізок М₁М₂ (рис.7), якщо

. (3.2)

Нехай задано  і координати точок і , знайдемо координати точки М (х, у).

З рис.7 і теореми про пропорційні відрізки, що відтинають паралельні прямі на сторонах кута, випливають співвідношення:

.

Оскільки числа х – х₁ і х₂ – х одного й того самого знака (при х₁ < х₂ вони додатні, а при х₁ > х₂ — від’ємні), то . Отже, . Звідси:

. (3.3)

Аналогічно одержимо формулу для знаходження координати у

. (3.4)

Наслідок. Якщо точка М (х, у) — середина відрізка М₁М₂, то  = 1 і формули (3.3), (3.4) мають вигляду:

. (3.5)

Приклад. Скласти рiвняння ГМТ, рiвновiдалених вiд точок , .

Нехай — довiльна точка ГМТ. За умовою задачi

.

Використовуючи формулу (3.1), маємо

Отже,

= ,

,

.

Таким чином, рiвняння ГМТ

.