Примеры
ПРИМЕР 1. Провести полное исследование
и построить график функции
.
1) Область определения функции
ℝ
.
2) Область определения функции симметрична относительно начала координат и
.
Следовательно, функция четная, и ее
график симметричен относительно оси
.
3) Функция имеет две точки разрыва:
и
.
Определим тип разрывов:
,
.
Итак, точка является точкой разрыва II рода, прямая – вертикальная асимптота графика функции.
Учитывая симметрию графика функции относительно оси , для точки получаем:
и
.
Следовательно, точка тоже является точкой разрыва II рода, прямая – вертикальная асимптота графика функции.
4) Функция определена при сколь угодно
больших
.
Следовательно, возможно существование
наклонных асимптот. При
имеем:
,
.
Следовательно, прямая
(т.е. прямая
)
является наклонной асимптотой правой
части графика функции. Та же прямая
будет наклонной асимптотой и для левой
части графика функции (так как график
функции симметричен относительно оси
).
5) Найдем точки пересечения графика с
осями координат. Пересечение с осью
:
⇒
,
⇒
,
⇒
Пересечение с осью :
⇒
Следовательно, график функции пересекает
обе координатные оси в начале координат
.
6) Найдем производную функции и критические точки первого рода. Имеем:
,
⇒ а)
при
;
б)
при
.
Таким образом, критической точкой первого рода является только точка .
Критическая точка
и точки разрыва
разбивают область определения функции
на четыре части. Определим знак производной
в каждой из них. Получим:
Следовательно, функция возрастает на
интервалах
и
,
функция убывает на интервалах
и
.
Точка
– точка максимума. Максимум функции:
.
7) Найдем вторую производную функции и критические точки второго рода. Имеем:
,
⇒ а)
при
;
б)
при
.
Таким образом, критических точек второго рода функция не имеет. Значит, график функции не имеет точек перегиба.
Точки разрыва разбивают область определения функции на три части. Определим знак второй производной в каждой из них. Получим:
Следовательно, график функции выпуклый
на интервале
,
график функции вогнутый на интервалах
и
.
8) На основании проведенного исследования строим следующий график:
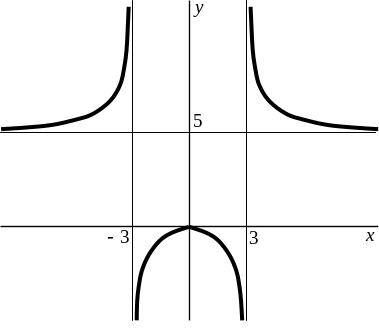
ПРИМЕР 2. Провести полное исследование
и построить график функции
.
1) Область определения функции ℝ.
2) Область определения функции симметрична относительно начала координат, но
,
⇒
и
.
Следовательно, функция общего вида и ее график не является симметричным относительно оси или начала координат.
3) Функция не имеет точек разрыва. Следовательно, график функции не имеет вертикальных асимптот.
4) Функция определена при сколь угодно больших . Следовательно, возможно существование наклонных асимптот. При имеем:
,
.
Следовательно, прямая
является наклонной асимптотой правой
части графика функции. Та же прямая
будет наклонной асимптотой и для левой
части графика функции, так как при
вычислении
и
мы будем в точности повторять все
действия, выполненные при вычислении
и
.
5) Найдем точки пересечения графика с осями координат. Пересечение с осью :
⇒
,
⇒
,
⇒
или
.
Пересечение с осью :
⇒
.
Следовательно, график функции пересекает
обе координатные оси в начале координат
и пересекает ось
еще и в точке
.
6) Найдем производную функции и критические точки первого рода. Имеем:
,
⇒ а)
при
;
б)
при
и
.
Таким образом, критическими точками
первого рода являются точки
,
,
.
Критические точки разбивают область определения функции на четыре части. Определим знак производной в каждой из них. Получим:
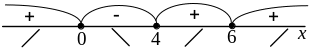
Следовательно, функция возрастает на
интервалах
и
,
функция убывает на интервале
.
Точка
– точка максимума, точка
– точка минимума. Максимум функции и
минимум функции:
,
.
7) Найдем вторую производную функции и критические точки второго рода. Имеем:
,
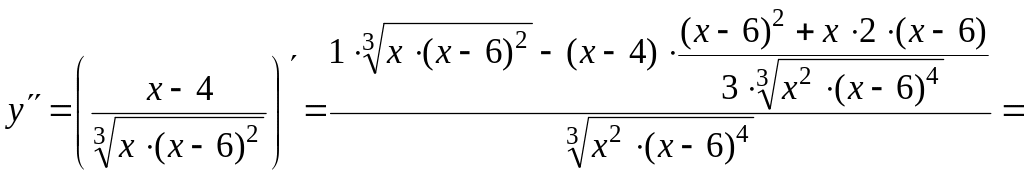
⇒ а)
при
;
б)
при
и
.
Таким образом, критическими точками второго рода являются точки , .
Критические точки разбивают область определения функции на три части. Определим знак второй производной в каждой из них. Получим:
Следовательно, график функции выпуклый
на интервале
,
график функции вогнутый на интервале
.
Точка
– точка перегиба графика функции.
8) На основании проведенного исследования строим следующий график:
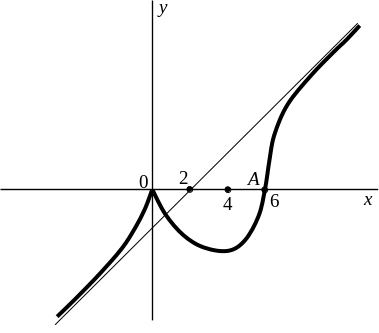
ПРИМЕР 3. Провести полное исследование
и построить график функции
.
1) Область определения функции
.
2) Область определения функции не симметрична относительно начала координат. Следовательно, функция общего вида и ее график не является симметричным относительно оси или начала координат.
3) Функция имеет две точки разрыва:
и
.
Определим тип разрывов:
,
.
Итак, точка
является точкой разрыва II
рода, прямая
– вертикальная асимптота графика
функции. Точка
является точкой разрыва первого рода.
4) Функция определена при сколь угодно больших положительных . Следовательно, возможно существование наклонной асимптоты для правой части графика. Имеем:
,
.
Следовательно, прямая
(т.е. прямая
)
является наклонной асимптотой правой
части графика функции.
5) График функции не пересекает оси
координат, так как
(⇒ не
пересечения с осью
)
и
(⇒ нет
пересечения с осью
).
6) Найдем производную функции и критические точки первого рода. Имеем:
,
⇒ а)
при
;
б)
при
и при
.
Таким образом, критических точек первого рода функция не имеет. Значит, функции не имеет экстремумов.
Точка разрыва разбивают область определения функции на две части. Определим знак производной в каждой из них. Получим:
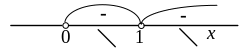
Следовательно, функция убывает на
интервалах
и
.
7) Найдем вторую производную функции и критические точки второго рода. Имеем:
,
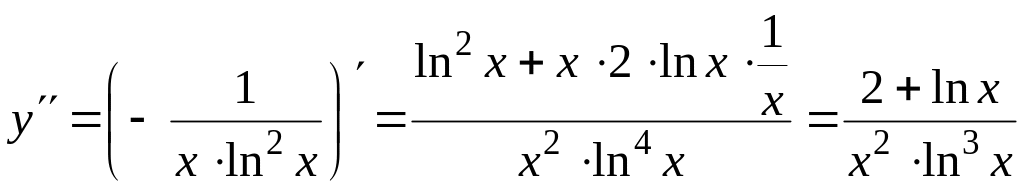⇒ а)
при
;
б) при и при .
Таким образом, критической точкой
второго рода является точка
.
Критическая точка и точка разрыва разбивают область определения функции на три части. Определим знак второй производной в каждой из них. Получим:
Следовательно, график функции выпуклый
на интервале
,
график функции вогнутый на интервалах
и
.
Точка
– точка перегиба.
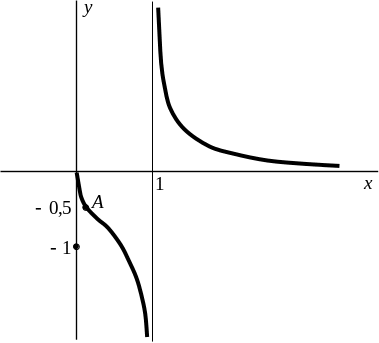
8) На основании проведенного исследования строим следующий график:
1 Иначе говоря, функция называется возрастающей на интервале , если большему значению аргумента из этого интервала соответствует большее значение функции.
2 Иначе говоря, функция называется убывающей на интервале , если большему значению аргумента из этого интервала соответствует меньшее значение функции.
3 см. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1, стр. 145.
4 см. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1, стр. 148.
5 см. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1, стр. 150-151.