
§10. Исследование функций и построение графиков §10. Исследование функций и построение графиков
1. Возрастание и убывание функции
ОПРЕДЕЛЕНИЕ. Функция
![]() называется возрастающей
(неубывающей) на интервале
называется возрастающей
(неубывающей) на интервале
![]() если для любых
если для любых
![]() таких, что
таких, что
![]() значения функции
значения функции
![]() и
и
![]() удовлетворяют неравенству
удовлетворяют неравенству ![]() 1
(
1
(![]() ).
).
Функция
называется убывающей
(невозрастающей) на интервале
если для любых
таких, что
значения функции
и
удовлетворяют неравенству
![]() 2
(
2
(![]() ).
).
Интервалы возрастания и убывания функции называются интервалами монотонности функции.
Из определения возрастающей функции
следует, что если
![]() возрастает на
,
то на этом интервале приращение аргумента
возрастает на
,
то на этом интервале приращение аргумента
![]() и соответствующее ему приращение
функции
и соответствующее ему приращение
функции
![]() будут иметь одинаковый знак.
будут иметь одинаковый знак.
Действительно, если
![]() ,
то
,
то
![]()
⇒
![]() ,
,
⇒
![]() .
.
Если
![]() ,
то
,
то
![]()
⇒
![]() ,
,
⇒
![]() .
.
Аналогично показывается, что если убывает на , то на этом интервале приращение аргумента и соответствующее ему приращение функции будут иметь разный знак.
Справедлива следующая теорема.
ТЕОРЕМА 1 (необходимое и достаточное условия возрастания (убывания) функции). Пусть функция дифференцируема на интервале . Тогда
1) если функция возрастает (убывает) на , то на этом интервале ее производная неотрицательна (неположительна),
т.е. ![]() ,
,
![]() (
(![]() ,
);
,
);
2) если производная
![]() на интервале
положительна (отрицательна), т.е.
на интервале
положительна (отрицательна), т.е.
![]() ,
(
,
(![]() ,
),
,
),
то функция на возрастает (убывает).
ДОКАЗАТЕЛЬСТВО3
1) (Необходимость.) Пусть возрастает на . Требуется доказать, что , .
Так как возрастает на , то знак и соответствующего ему приращения совпадают.
⇒
![]() ,
,
,
,
![]()
(при условии, что
![]() ).
).
Но тогда ![]() .
.
Аналогично доказывается, что если убывает на , то , .
2) (Достаточность.) Пусть , . Требуется доказать, что возрастает на .
Пусть
,
.
Рассмотрим разность
![]() .
По теореме Лагранжа, существует точка
.
По теореме Лагранжа, существует точка
![]() ,
такая, что
,
такая, что
![]() .
.
⇒
![]() .
.
Так как
![]() и
и
![]() получаем:
получаем:
![]() ,
,
![]() .
.
Следовательно, возрастает на интервале .
Аналогично доказывается, что если , , то убывает на . ∎
2. Экстремумы функции
Пусть функция
определена на множестве
![]() ℝ,
ℝ,
![]() ,
,
![]() – внутренняя точка
– внутренняя точка
![]() (т.е. существует некоторая окрестность
точки
,
целиком лежащая во множестве
).
(т.е. существует некоторая окрестность
точки
,
целиком лежащая во множестве
).
ОПРЕДЕЛЕНИЕ. Точка
![]() называется точкой максимума
функции
если существует такая
называется точкой максимума
функции
если существует такая
![]() -окрестность
-окрестность
![]() точки
,
что
точки
,
что
![]() ,
,
![]() .
Значение функции в точке максимума
называется максимумом функции.
.
Значение функции в точке максимума
называется максимумом функции.
Точка
называется точкой минимума
функции
если существует такая
-окрестность
точки
,
что
![]() ,
.
Значение функции в точке минимума
называется минимумом функции.
,
.
Значение функции в точке минимума
называется минимумом функции.
Точки минимума и максимума функции называются ее точками экстремума. Минимумы и максимумы функции называются ее экстремумами.
Замечания:
1 )
Понятия минимум и максимум функции
близки к понятиям наименьшее и наибольшее
значения функции. По сути, они отражают
одно свойство функции: они показывают,
в каком отношении находятся значение
функции в данной точке и значения функции
в других точках. Различие в области
действия этих понятий. Наибольшее и
наименьшее значения – понятия
глобального характера («
)
Понятия минимум и максимум функции
близки к понятиям наименьшее и наибольшее
значения функции. По сути, они отражают
одно свойство функции: они показывают,
в каком отношении находятся значение
функции в данной точке и значения функции
в других точках. Различие в области
действия этих понятий. Наибольшее и
наименьшее значения – понятия
глобального характера («![]() »),
максимум и минимум – понятия локального
характера («
»).
Чтобы подчеркнуть эту взаимосвязь
понятий, в некоторой литературе
употребляют термины «глобальный максимум
(минимум)» вместо наибольшего (наименьшего)
значения функции и «локальный максимум
(минимум)» – вместо максимум (минимум)
функции.
»),
максимум и минимум – понятия локального
характера («
»).
Чтобы подчеркнуть эту взаимосвязь
понятий, в некоторой литературе
употребляют термины «глобальный максимум
(минимум)» вместо наибольшего (наименьшего)
значения функции и «локальный максимум
(минимум)» – вместо максимум (минимум)
функции.
2) В силу локального характера понятий максимума и минимума, функция может иметь в своей области определения несколько точек максимума и минимума. Причем, некоторые минимумы функции могут быть больше ее максимумов (см. рис. 1).
Для функции, дифференцируемой в точке , справедлива следующая теорема.
ТЕОРЕМА 2 (необходимое условие экстремума, теорема Ферма). Если – точка экстремума функции и – дифференцируема в точке , то ее производная в этой точке равна нулю.
Г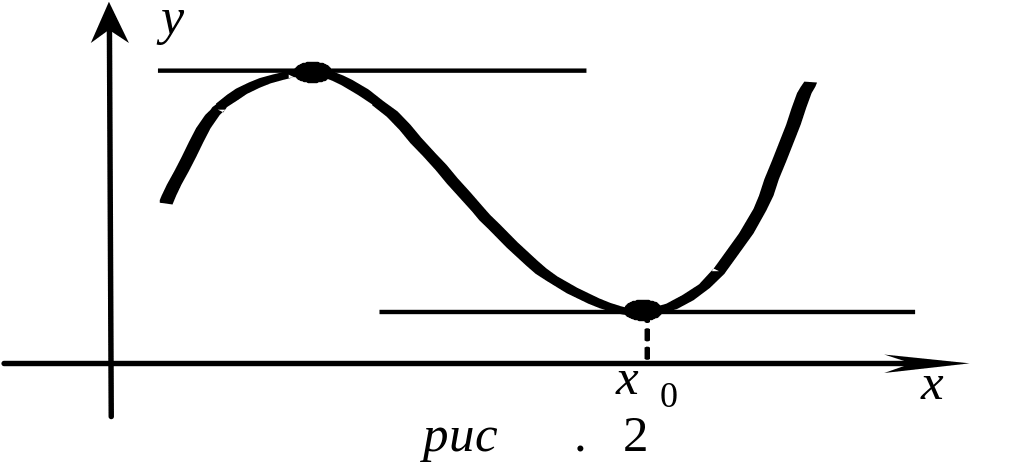 еометрический
смысл теоремы 2. Если
– точка экстремума функции
и кривая
еометрический
смысл теоремы 2. Если
– точка экстремума функции
и кривая
![]() имеет невертикальную касательную в
точке
имеет невертикальную касательную в
точке
![]() ,
то эта касательная – горизонтальная
(см. рис 2).
,
то эта касательная – горизонтальная
(см. рис 2).
ДОКАЗАТЕЛЬСТВО4
Пусть, для определенности
![]() – точка максимума функции. Так как
– дифференцируема в точке
,
то существуют
– точка максимума функции. Так как
– дифференцируема в точке
,
то существуют
![]() и
и
![]() ,
причем
,
причем
![]() .
.
По определению
![]() ,
,
![]() .
.
Так как
– точка максимума функции, то
![]() в некоторой окрестности точки
.
в некоторой окрестности точки
.
⇒
![]()
и ![]() при
при
![]() ,
,
![]() при
при
![]() .
.
Следовательно,
![]() ,
,
![]() .
.
Итак, получили:
![]() ,
,
![]()
и .
Но это возможно только при
![]() .
∎
.
∎
Точки, в которых производная функции равна нулю, называются стационарными точками функции .
Очевидно, что не любая стационарная
точка функции является ее точкой
экстремума. Например, функция
![]() имеет стационарную точку
имеет стационарную точку
![]() ,
которая не является ее точкой экстремума.
Для функции, дифференцируемой в точке
,
справедлива следующая теорема.
,
которая не является ее точкой экстремума.
Для функции, дифференцируемой в точке
,
справедлива следующая теорема.
ТЕОРЕМА 3 (первое достаточное условие экстремума функции). Пусть – внутренняя точка области определения функции , непрерывна в окрестности точки и дифференцируема в некоторой ее окрестности, за исключением, возможно, самой точки . Если при переходе через точку производная функции меняет знак, то является точкой экстремума. При этом, если производная меняет знак с плюса на минус, то – точка максимума, если с минуса на плюс – то – точка минимума.
ДОКАЗАТЕЛЬСТВО5
Пусть, например, при переходе через
точку
производная
![]() меняет знак с плюса на минус.
меняет знак с плюса на минус.
По формуле Лагранжа для любой точки
![]() из некоторой окрестности
точки
справедливо равенство
из некоторой окрестности
точки
справедливо равенство
![]() ,
,
где
![]() – некоторая точка, лежащая между
и
.
Используя это равенство, определим
знак
– некоторая точка, лежащая между
и
.
Используя это равенство, определим
знак
![]() .
Имеем:
.
Имеем:
1) если
![]() ,
то
,
то
![]() ,
,
![]()
и ![]() ;
;
2) если
![]() ,
то
,
то
![]() ,
,
![]()
и .
Таким образом, для любой точки из некоторой окрестности точки выполняется неравенство
![]()
и, следовательно, точка является точкой максимума функции .
Аналогично доказывается, что если при переходе через точку производная меняет знак с минуса на плюс, то точка является точкой минимума функции . ∎
Замечание. Из теоремы 3 следует, что точками экстремума могут быть не только стационарные точки, но и точки, в которых функция не имеет производной (точки разрыва производной).
Стационарные точки функции и точки, в которых производная функции не существует, называются критическими точками I рода (критическими точками по первой производной).
ПРИМЕР. Найти экстремумы функции
![]() .
.
РЕШЕНИЕ
1) Находим область определение функции:
![]() ℝ.
ℝ.
2) Находим производную функции и ее критические точки:
![]() ;
;
![]() :
:
![]() ,
⇒
,
⇒
![]() ,
,
![]() ;
;
![]() :
таких точек нет.
:
таких точек нет.
3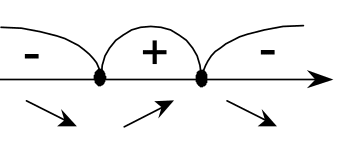 )
Определяем знак
)
Определяем знак
![]() :
:
Таким образом,
– точка минимума функции ,
– точка максимума функции ,
![]() ,
,
![]() .
.
Если функция
![]() раз дифференцируема в критической
точке
,
то справедлива следующая теорема.
раз дифференцируема в критической
точке
,
то справедлива следующая теорема.
ТЕОРЕМА 4 (второе достаточное условие экстремума функции). Пусть – внутренняя точка области определения функции и раз дифференцируема в точке , причем
![]() ,
,
![]() .
.
Тогда: 1) если
– четное и
![]() ,
то
является точкой минимума функции
;
,
то
является точкой минимума функции
;
2) если
– четное и
![]() ,
то
является точкой максимума функции
;
,
то
является точкой максимума функции
;
3) если – нечетное, то не является точкой экстремума функции .
Замечание. На практике пользоваться
вторым достаточным условием экстремума
функции менее удобно, чем первым. Это
связано с тем, что 1) не всегда легко
вычислить
![]() ;
2) поведение функции (возрастание и
убывание) определяется не на всех
интервалах области определения. Но
иногда, все же лучше применить второе
достаточное условие. Например, если
критических точек бесконечно много.
;
2) поведение функции (возрастание и
убывание) определяется не на всех
интервалах области определения. Но
иногда, все же лучше применить второе
достаточное условие. Например, если
критических точек бесконечно много.
ПРИМЕР. Найти экстремумы функции
![]() .
.
РЕШЕНИЕ
1) Находим область определение функции:
ℝ.
2) Находим производную функции и ее критические точки:
![]() ;
;
:
![]() ⇒
⇒
![]() ,
,
![]() ℤ;
ℤ;
: таких точек нет.
3) Находим вторую производную функции и вычисляем ее в критических точках:
![]() ,
,
![]()
Таким образом, функция имеет максимумы в точках
![]() (
(![]() ℤ),
ℤ),
![]() ;
;
и имеет минимумы в точках
![]() (
ℤ),
(
ℤ),
![]() .
.
СХЕМА ПОЛНОГО ИССЛЕДОВАНИЯ ФУНКЦИИ
Найти область определения функции.
Исследовать четность и периодичность функции.
Исследовать точки разрыва, найти вертикальные асимптоты.
Найти наклонные асимптоты (если их существование возможно).
Найти точки пересечения графика с осями координат.
Найти
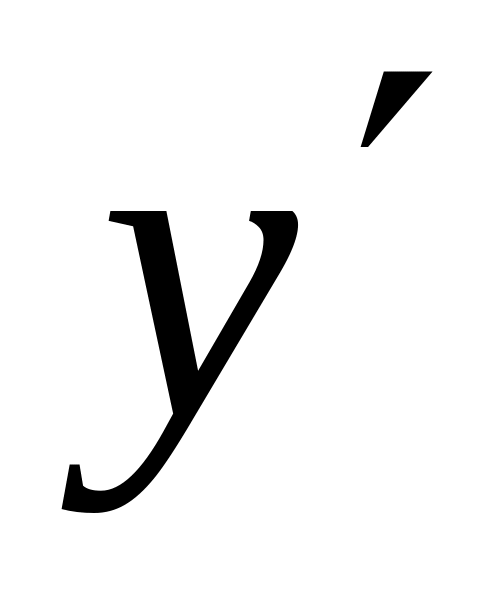 .
Определить точки экстремума, интервалы
возрастания и убывания функции.
.
Определить точки экстремума, интервалы
возрастания и убывания функции.Найти
 .
Определить точки перегиба графика,
интервалы его выпуклости и вогнутости.
.
Определить точки перегиба графика,
интервалы его выпуклости и вогнутости.Построить график функции.
