Лекция 6. Адсорбция

6.1. Основные определения. Изотерма адсорбции. 6.2. Уравнение Гиббса. 6.3. Поверхностно-активные вещества. 6.4. Правило Дюкло-Траубе. Уравнение Шишковского.

Из II начала термодинамики вытекает важный вывод: любая система стремится минимизировать свою энергию за счет необратимых самопроизвольных процессов.

При диспергировании затрачивается работа на создание поверхности раздела фаз. Она концентрируется на поверхности раздела фаз в виде свободной поверхностной энергии Гиббса. Эта энергия зависит от площади раздела фаз и сил взаимодействия между молекулами, находящимися на поверхности раздела фаз:

G^(s) = σ S (6.1)

где S – площадь поверхности раздела фаз, м²; σ – удельная поверхностная энергия или свободная энергия единицы поверхности, Дж/м².

Поверхностную энергию можно уменьшить за счет уменьшения площади поверхности раздела фаз, т.е. укрупнения частиц дисперсной фазы. Это приведет к тому, что сила тяжести (если плотность фазы больше плотности среды) или сила выталкивания (если плотность фазы меньше плотности среды) станет меньше сил броуновского движения. В результате частицы дисперсной фазы или оседают или всплывают.

Для растворов состоящих из двух или нескольких веществ, различающихся интенсивностью взаимодействия между молекулами (полярностью), уменьшения величины G^(s) можно достичь за счет уменьшения σ. Действительно, менее полярный компонент будет переходить из объема в поверхностный слой, поскольку накопление менее полярного компонента приведет к уменьшению межмолекулярного взаимодействия на поверхности раздела фаз, а следовательно, к уменьшению удельной поверхностной энергии и свободной поверхностной энергии G^(s). В результате в поверхностном слое происходит концентрация менее полярного компонента, т.е. адсорбция

6.1. Основные определения. Изотерма адсорбции

Адсорбцией называется сгущение газообразного или растворенного вещества на поверхности раздела фаз. Газ или растворенное вещество принято называть адсорбтивом (или адсорбатом), а жидкость или твердое тело, адсорбировавшее их - адсорбентом.

Так как адсорбция является поверхностным явлением, то, естественно, она имеет огромное значение для коллоидных систем, обладающих большой поверхностью.

Различают физическую, или ван-дер-ваальсовую, адсорбцию и химическую адсорбцию, или хемосорбцию. В первом случае адсорбционные силы имеют ту же природу, что и межмолекулярные, или ван-дер-ваальсовые, силы. Физическая адсорбция всегда обратима. При химической адсорбции адсорбционные силы имеют химическую природу. Хемосорбция обычно необратима. Мы будем рассматривать, главным образом, физическую адсорбцию.

Физическая адсорбция протекает самопроизвольно. Адсорбтив стремится занять всю поверхность адсорбента, но этому препятствует процесс противоположный адсорбции - десорбция, вызванная стремлением к равномерному распределению вещества вследствие теплового движения.

Для каждой концентрации адсорбтива в окружающей среде существует состояние адсорбционного равновесия. Понятно, что чем выше концентрация адсорбтива, тем больше адсорбция. Для каждой температуры также существует свое состояние равновесия. Чем выше температура, тем меньше физическая адсорбция. Это согласуется с принципом Ле Шателье-Брауна, поскольку десорбция сопровождается поглощением тепла.

Количественно адсорбция может быть выражена с помощью следующих величин:

1. Величиною (а), представляющей количество адсорбтива, находящегося в объеме адсорбционного слоя, отвечающего единице массы адсорбента. Эту величину обычно измеряют в моль/г.

2. Величиною (α), равной количеству адсорбированного вещества, приходящегося на единицу поверхности адсорбента. Эта величина - поверхностная концентрация адсорбтива. Единица измерения - моль/м² или ммоль/см².

3. Введенной Гиббсом величиной Г, представляющей собой избыток числа молей адсорбтива в объеме поверхностного слоя площадью 1 см² по сравнению с числом его молей в том же объеме, если бы у межфазной границы не происходило изменения концентрации адсорбтива. При малых концентрациях адсорбтива (Г) близка к (α), при больших - величина (Г) отличается от (α).

Адсорбцию можно характеризовать:

1. зависимостью (а) от температуры при постоянных равновесных давлении (р) или (с); графики а = f (T) при p = const - изобары, а при с = const - изопикны;

2. зависимостью равновесного давления (или концентрации) от температуры при постоянном количестве адсорбированного вещества графики р = f (T) и с = f (T) при а = const - изостеры;

3. зависимостью (а) от (р) или (с) при постоянной температуре; графики а = f (р) или а = f (с) при Т = const - изотермы.

Изотермы имеют особенно большое значение при изучении адсорбции, поэтому целесообразно ограничится рассмотрением именно этой зависимости.

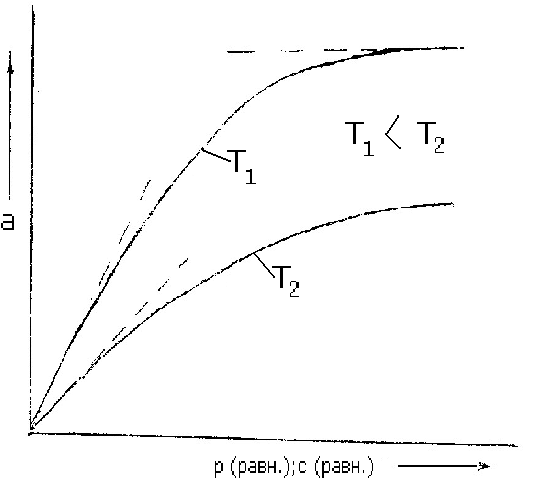
рис. 6.1

Как можно видеть из схематического изображения обычных изотерм адсорбции (рис. 6.1), они имеют три участка. Начальный, почти прямолинейный участок, показывает, что при малых давлениях или концентрациях адсорбция почти пропорциональна этим величинам. Почти горизонтальный участок, соответствующий большим давлениям или концентрациям, отвечает поверхности адсорбента, полностью насыщенной адсорбтивом. Средний участок кривой соответствует промежуточным степеням заполнения поверхности.

Изотерма адсорбции по виду напоминает параболу, поэтому Бедекер, а затем Фрейндлих для ее аналитического выражения предложили эмпирическое уравнение вида:

(6.2)

где х – количество адсорбированного вещества;

m – масса адсорбента;

p – равновесное давление газа в системе;

К и - константы.

Для адсорбции из раствора уравнение Фрейндлиха пишется в таком виде:

(6.3)

где β – константа, соответствующая константе К уравнения (6.2);

с – равновесная концентрация.

Константа β представляет собой величину адсорбции при равновесной концентрации адсорбтива, равной 1 моль/л. Константы уравнения Фрейндлиха можно найти графически по изотерме в логарифмических координатах. Уравнение Фрейндлиха пригодно только для интервала средних давлений и концентраций.