6 Розв’язання диференціальних рівнянь

6.1 Методи розв'язку диференціальних рівнянь

В інженерній практиці часто доводиться досліджувати динаміку тих чи інших технічних об’єктові. Для цього створюють математичні моделі, які у більшості випадків мають вигляд диференціальних рівнянь. Для отримання відомостей про властивості технічних об’єктів необхідно знати розв’язки їх моделей. Отримати аналітичний розв’язок таких моделей можна тільки в окремих випадках. У переважній більшості для розв’язку диференціальних рівнянь застосовують числові методи.

Метод Ейлера. Він має обмежене застосування із-за великої похибки, яка накопичується в процесі обчислень.

Отже, будемо розглядати звичайне диференціальне рівняння першого порядку:

(6.1)

З початковою умовою

, (6.2)

де - деяка відома у загальному випадку, нелінійна функція двох аргументів.

Будемо вважати, що для даної задачі (6.1), (6.2), яка носить назву задачі Коші, виконуються вимоги, які забезпечують існування і єдиність на відрізку її розв’язку . Допустимо, що і неперервні. Використовуючи теорему Тейлора, розкладемо функцію у ряд Тейлора в околі точки . Для кожного значення існує таке , яке лежить між і , що . У відповідності з (6.1) . Тому

.

Нехай і , а - точка, яка лежить між і . Тоді

.

Якщо довжина кроку h вибрана досить малою, то членом другого порядку можна знехтувати і отримати

, (6.3)

де ; .

Ітераційна процедура (6.3) і є наближенням Ейлера для задачі (6.1), (6.2) при цьому .

Як випливає із формули (6.3) кожна наступна ордината, починаючи із , обчислюється шляхом додавання до неї площі прямокутника (рис. 6.1).

Рисунок 6.1 – Процес утворення прямокутників в ітераційній процедурі (6.3)

При виводі ітераційної формули Ейлера для кожного кроку обчислень ми нехтували величиною , що приводить до накопичування похибки і після N кроків вона складе величину

,

де ; - інтервал, на якому шукають розв’язок задачі Коші;

- похибка першого порядку.

Для розв’язку диференціального рівняння (6.1) з початковою умовою (6.2) методом Ейлера може бути використана процедура MethodEuler.

MethodEuler^*

Числовий розв'язок диференціального рівняння методом ейлера

Вхід:n-кількість вузлів дискретності

t0-початкове значення часу

tk-кінцеве значення часу

y0- початкова умова

Вихід:y(k)-значення ординат функції у вузлах дискретизації

t-вектор абсцис

Значення функції рівняння (6.1) обчислюється підпроцедурою - fun_Eiler.

Обчислення кроку дискретизації

1 h=(tk-t0)/n

Числовий розв'язок задачі

2 CФормувати нульовий вектор y розміром n+1

3 y(1)=y0

4 for k=1 to n

5 y_k=fun_Eiler(y(k))

6 y(k+1)=y(k)+h*y_k

7 end for

8 t(1)=t0

9 for i=2 to n

10 t(i)= y0+(i-1)*h

11 end for

12 return t,y

Метод Гюна. Проінтегруємо ліву і праву частини рівняння (6.1) в межах від до :

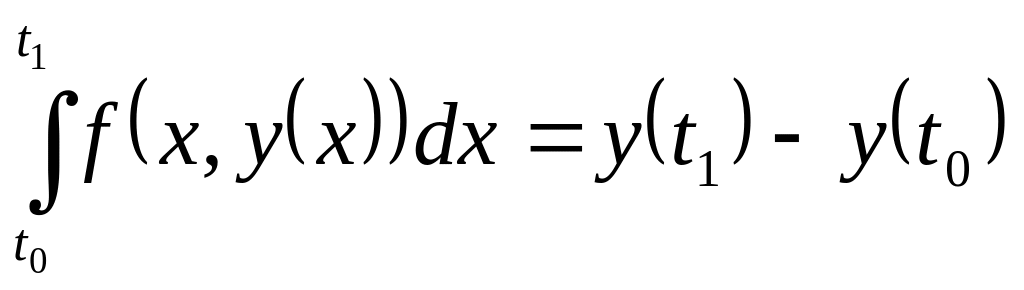. (6.4)

Із рівняння (6.4) знайдемо

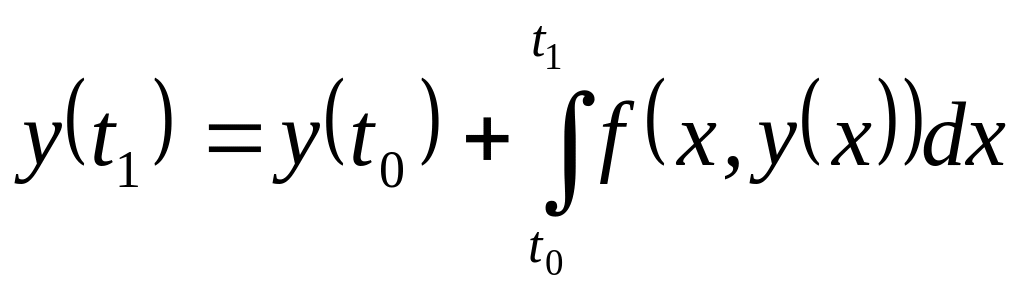. (6.5)

Інтеграл, який знаходиться у правій частині рівняння (6.5), можна наближено обчислити за формулою трапецій (рис. 6.1).

. (6.6)

Права частина рівняння (6.6) вимагає значення , яке знайдемо, скориставшись методом Ейлера. Із формули (6.3) для отримаємо

.

З врахуванням значення формула (6.1) набуде такого вигляду:

.

Тепер, зробивши заміну , , генеруємо процес розв’язку задачі Коші (6.1).

Для k-го кроку обчислень будемо мати

, , (6.7)

, (6.8)

, ... .

Залишковий член у формулі трапецій, який використовують для наближення інтервалу в (6.6), дорівнює

. (6.9)

У процесі обчислень на кожному кроці накопичується похибка (6.9) і після N кроків накопичень похибка методу Гюна буде такою:

,

тобто метод Гюна має другий порядок точності . Нижче наведена процедура MethodHeun, за допомогою якої можна розв’язати диференціальне рівняння (6.1) з початковою умовою (6.2) методом Гюна.

MethodHeun^*

Метод Гюна розв'язку задачі Коші y'=f(t,y)

Вхід:f(t,y)-функція, значення якої задається підпроцедурою fun_Heun

to,tk-початкова і кінцева точки інтегрування

y0-початкова умова

n-число ітерацій

Вихід:t-вектор абсцис

y-вектор ординат

Обсилюємо крок h та ініціалізуємо вектори t,y

1 h=(tk-t0)/n

2 CФормувати нульовий вектор y розміром n+1

Ітераційна процедура методу Гюна

3 y(1)=y0

4 t(1)=t0

5 for i=2 to n

6 t(i)=t0+(i-1)*h

7 end for

8 for k=1 to n

9 k1=fun_Heun(t(k),y(k))

10 k2=fun_Heun(t(k+1),y(k)+h*k1)

11 y(k+1)=y(k)+(h/2)*(k1+k2)

12 end for

13 return t,y

Метод Рунге-Кутта.

Ідея побудови методів Рунге-Кутта р-го порядку полягає в отриманні наближеного числового розв’язку задачі Коші за формулою

, (6.10)

де - деяка функція, яка наближує частину ряду Тейлора до р-го порядку і не вміщує часткових похідних функції .

Якщо в (6.10) замінити на , то отримаємо метод Ейлера, тобто метод Ейлера можна вважати частковим випадком методів Рунге-Кутта, коли .

Для побудови методів Рунге-Кутта вище першого порядку функцію вибирають як таку, що залежить від певних параметрів, які вибирають шляхом порівняння виразу (6.10) з многочленом Тейлора для з бажаним порядком степені.

Розглянемо випадок р=2 і візьмемо функцію з наступною структурою:

(6.11)

Розкладемо функцію двох змінних в ряд Тейлора, обмежившись лише лінійними членами

.(6.12)

В (6.11) функцію замінимо її наближеним значенням (6.12). У результаті будемо мати

,

де , .

Підставивши останній вираз в (6.10), отримаємо

. (6.13)

Розкладемо тепер функцію в ряд Тейлора, враховуючи члени першого і другого порядків

. (6.14)

Оскільки , то .

Знайдемо другу похідну . За формулою повної похідної будемо мати

.

Враховуючи значення , отримаємо

.

Отже,

.

Тепер значення і можемо підставити у вираз (6.14). У результаті отримаємо

. (6.15)

Порівнюючи між собою вирази (6.13) і (6.15) приходимо до висновку, що

Отримана система із трьох рівнянь, яка вміщує чотири невідомих. Це означає, що один із параметрів вільний і його можна вибрати довільним. Візьмемо , . Тоді

, .

У результаті підстановки значень і у формулу (6.11) отримаємо:

.

Отриманий результат дає підставу ітераційну процедуру (6.10) записати у такому вигляді:

. (6.16)

Якщо в (6.16) , то

, (6.17)

а при маємо

. (6.18)

Ітераційна процедура (6.17) носить назву метода Хойна, а (6.18) – породжує метод середньої точки.

Аналіз методів Рунге-Кутта другого порядку дає уявлення в якій формі слід шукати метод Рунге-Кутта довільного порядку.

За аналогією з (6.18) можемо записати

,

, , (6.19)

.

Найпоширенішим із сімейства методів (6.17) є метод четвертого порядку (р=4) або просто метод Рунге-Кутта, який породжує таку ітераційну процедуру:

,

,

, (6.20)

,

.

Метод Рунге-Кутта дає похибку накопичення четвертого порядку - .

Бажання підвищити точність методу Рунге-Кутта призвело до появи різних його версій. Одна із них – метод Кутта-Мерсона з вибором кроку на кожній із ітерацій.

На k-му кроці розв’язку задачі Коші послідовно обчислюють:

,

,

, (6.21)

,

,

,

.

Після цього підраховують величину , якщо , то вважають, що в точці отриманий розв’язок задачі Коші з точністю . У тому випадку, коли крок h зменшують вдвічі і знову обчислюють значення .

При переході до наступного кроку здійснюється перевірка на можливість збільшення кроку. Якщо , то .

Процедура MethodRunge-Kutt дає змогу розв’язати диференціальне рівняння (6.1) з початковою умовою (6.2) методом Рунге-Кутта.

MethodRunge-Kutt^*

%Метод Рунге-Кутта розв'язку y'=f(t,y) задачі Коші на

інтервалі [t0tk] з початковою умовою y(0)=y0

Вхід:f(t,y)-функція, значення якої задати у підпроцедурі fun_RK

to,tk-початкова і кінцева точки інтегрування

y0-початкова умова

n-число ітерацій

Вихід:t-вектор абсцис

y-вектор ординат

Обсилюємо крок h та ініціалізуємо вектор y

1 h=(tk-t0)/n

2 CФормувати нульовий вектор y розміром n+1

Ітераційна процедура методу Рунге-Кутта

3 y(1)=y0

4 t(1)=t0

5 for i=2 to n

6 t(i)=t0+(i-1)*h

7 end for

8 for k=1 to n

9 f1=fun_RK(t(k),y(k))

10 f2=fun_RK(t(k)+h/2,y(k)+h*f1/2)

11 f3=fun_RK(t(k)+h/2,y(k)+h*f2/2)

12 f4=fun_RK(t(k)+h,y(k)+h*f3)

13 y(k+1)=y(k)+(f1+2*f2+2*f3+f4)*h/6

14 end for

15 return t,y