МЕТОДИ ОБЧИСЛЕНЬ

4 Задачі лінійної алгебри

4.1 Розв’язок систем лінійних рівнянь

Будемо розглядати системи лінійних рівнянь, в яких число невідомих співпадає з числом рівнянь у системі при цьому допускаємо, що існує єдиний розв’язок такої системи.

Отже, вивчається питання про чисельний розв’язок системи такого виду:

(4.1)

де - дійсні коефіцієнти системи;

вільні члени системи.

Систему рівнянь (4.1) можна подати компактніше, якщо ввести квадратну матрицю, елементами якої є коефіцієнти

.

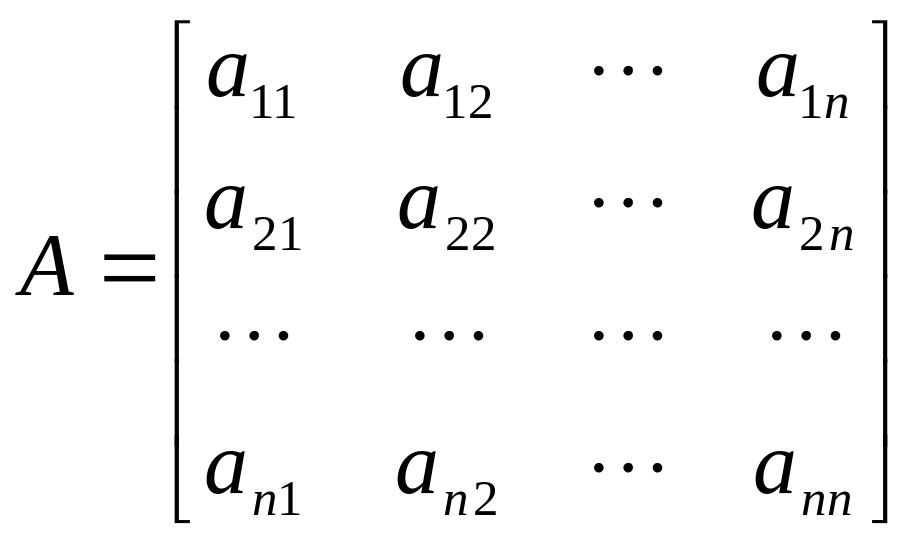Тоді система (4.1) буде еквівалентною наступному матричному рівнянню:

(4.2)

де вектор невідомих;

вектор вільних членів системи.

Ефективність способів розв’язку системи (4.1) багато залежить від структури і властивостей матриці розміру, обумовленості, симетричності, наповненості (тобто від співвідношення між нульовими і ненульовими елементами), місця і специфіки розміщення ненульових елементів та ін.

Якщо система рівнянь (4.1) має невелике число змінних , то для її розв’язку застосовують формулу Крамера

(4.3)

де - детермінант матриці в якій тий стовпець замінений вільними членами;

- детермінант матриці .

Інший спосіб розв’язку системи рівнянь (4.1), який по суті еквівалентний (4.3), це знаходження безпосередньо із рівнянням (4.2) шляхом множення зліва лівої і правої частин рівнянь (4.2) на матрицю , що є оберненою до матриці

. (4.4)

Не дивлячись на простоту формул (4.3) і (4.4), воно є непридатним для систем з великим числом невідомих, оскільки число машинних операцій множення зв’язаних з обчисленням детермінанта матриці або її оберненням пропорційно факторіалу числа невідомих . Наприклад, при і при швидкодії ЕОМ 10⁹ (операцій множення)/с на розв’язок такої системи необхідно приблизно затратити 10¹⁴¹ років, що робить нереальним застосування формул (4.3), (4.4) для систем великої розмірності .

Метод Гауса з вибором головного елемента. Ідея методу Гауса полягає в приведенні матриці до верхньої, (нижньої) трикутної матриці у результаті чого система рівнянь (4.1) набуде також вигляду:

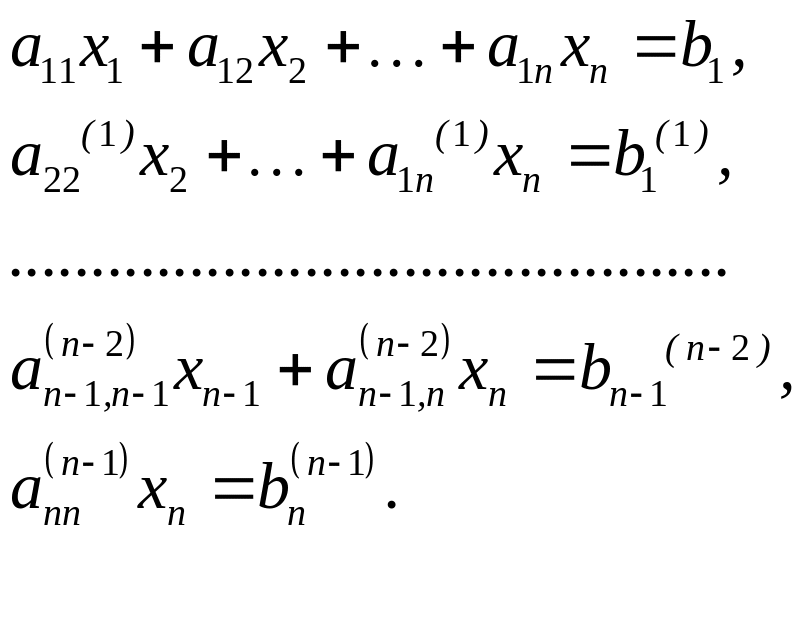(4.5)

Останнє рівняння системи (4.5) має тільки одне невідоме і його легко розв’язати відносно

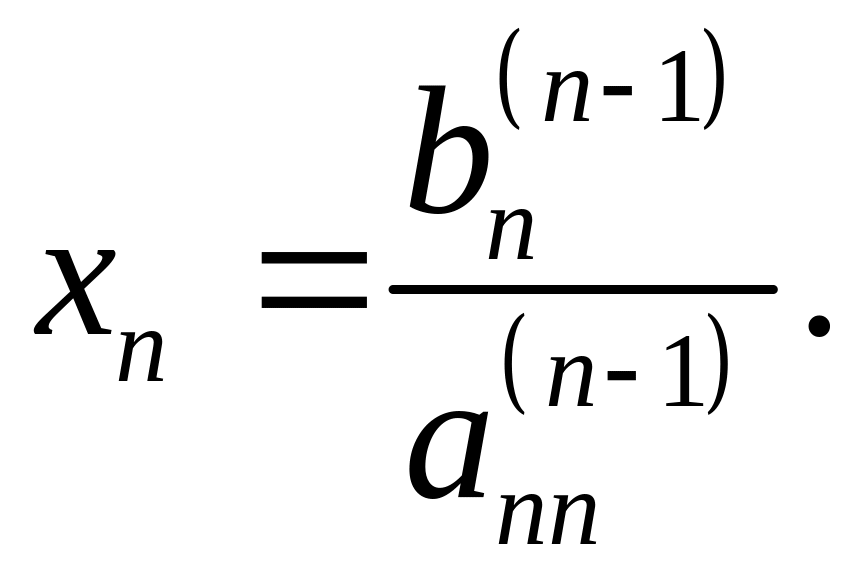
Оскільки тепер відомо, то його можна підставити в передостаннє рівняння і знайти

.

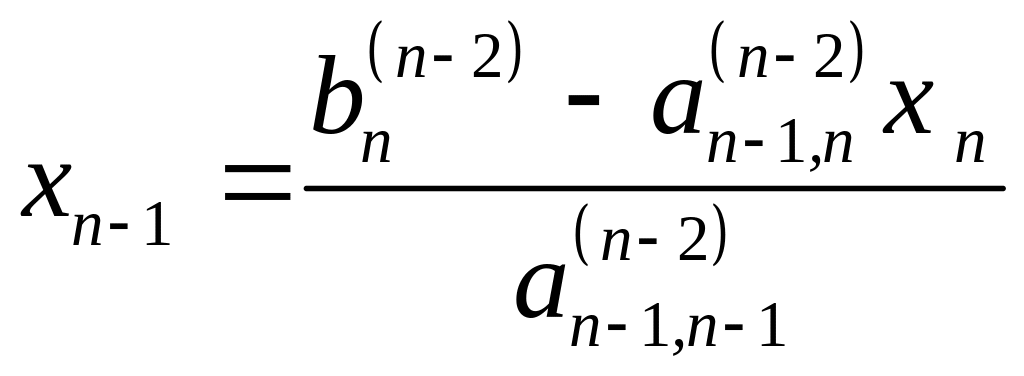Продовжуючи цей процес, на тому етапі так званого зворотного ходу Гауса, отримаємо

, . (4.6)

Сума у формулі (4.6) за визначенням дорівнює нулеві, якщо нижній індекс суми більший за верхній.

Тепер задача полягає у приведені матриці до діагонального вигляду. Це робиться послідовним виключенням спочатку із другого, третього ,…, го рівнянь, потім із третього, …, го рівнянь, із , …, го рівнянь і т. д.

На першому етапі перше рівняння помножимо на коефіцієнт і додамо його до другого рівняння; потім перше рівняння множимо на коефіцієнт і додаємо до третього рівняння і т.д.; на му кроці перше рівняння множимо на і додаємо до того рівняння.

Отже, після 1 кроків отримаємо систему рівнянь:

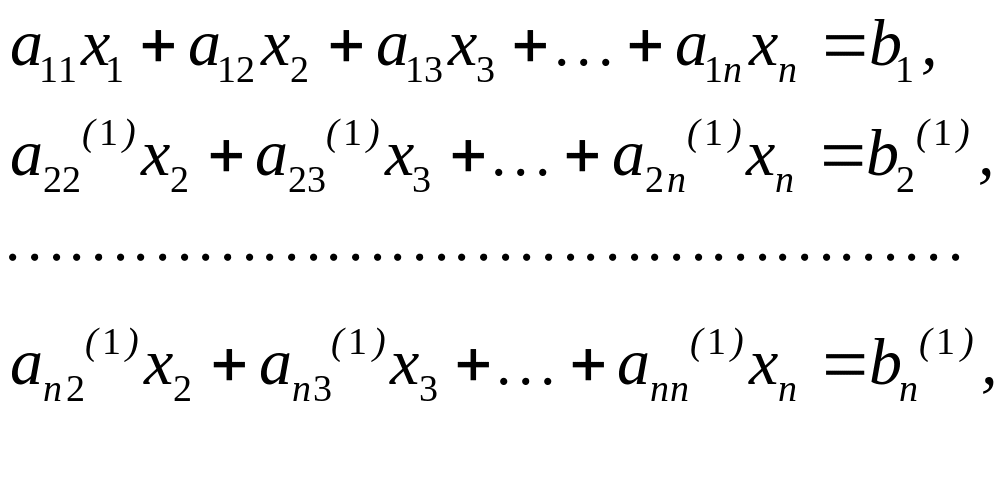(4.7)

яка буде еквівалентною (4.1).

Нові коефіцієнти системи (4.7) (з верхнім індексом «1») перераховуються за формулами:

, , де

При цьому ми вважаємо, що оскільки система має єдиний розв’язок і не всі коефіцієнти дорівнюють нулю. Це значить, що завжди рівняння з ненульовим коефіцієнтом при змінній можна поставити першим.

На другому етапі виключають змінну із третього і наступних рівнянь, виконуючи аналогічні операції, що і на першому етапі. У результаті отримують

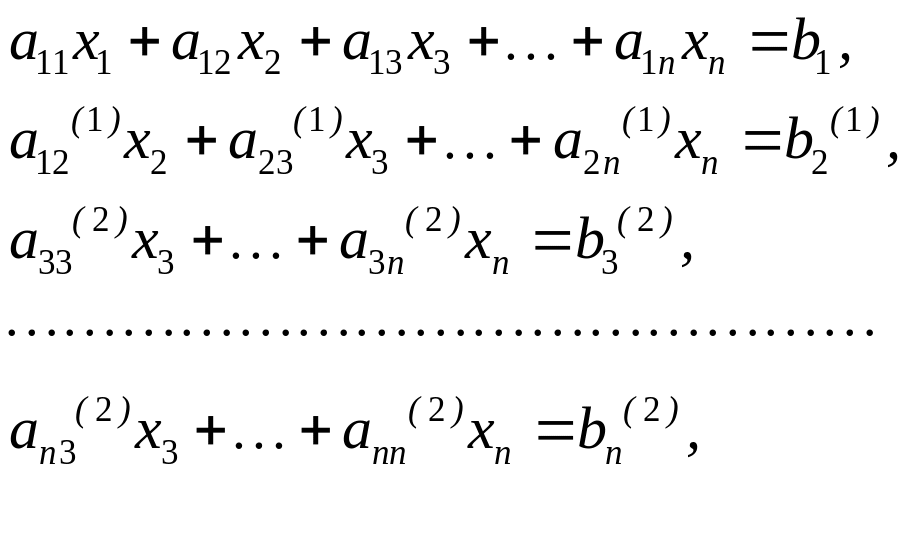
де

Процес послідовного виключення змінних можна продовжити і на кроці отримаємо систему рівнянь (4.5), в якій

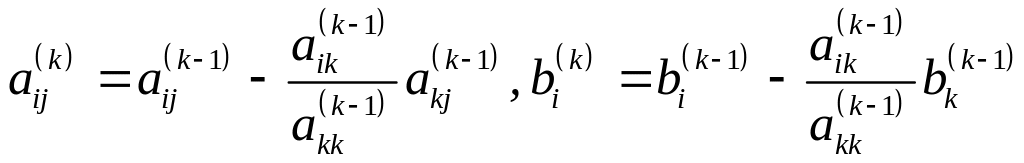, (4.8)

, , . Нижні індекси змінюються від до .

Для полегшення запам’ятовування формул можна скористатись правилом прямокутника (рис. 3.9), на основній діагоналі якого розміщені коефіцієнти і , а на допоміжній коефіцієнти і . Тоді коефіцієнти для наступної ітерації обчислюються як різниці добутків коефіцієнтів основної та допоміжної діагоналей, що діляться на коефіцієнт . За таким же правилом перераховуються і вільні коефіцієнти системи. Різниця лише у тому, що на схемі, яка наведена на рис. 4.1, коефіцієнт необхідно замінити на , а на .

Степінь складності алгоритму .

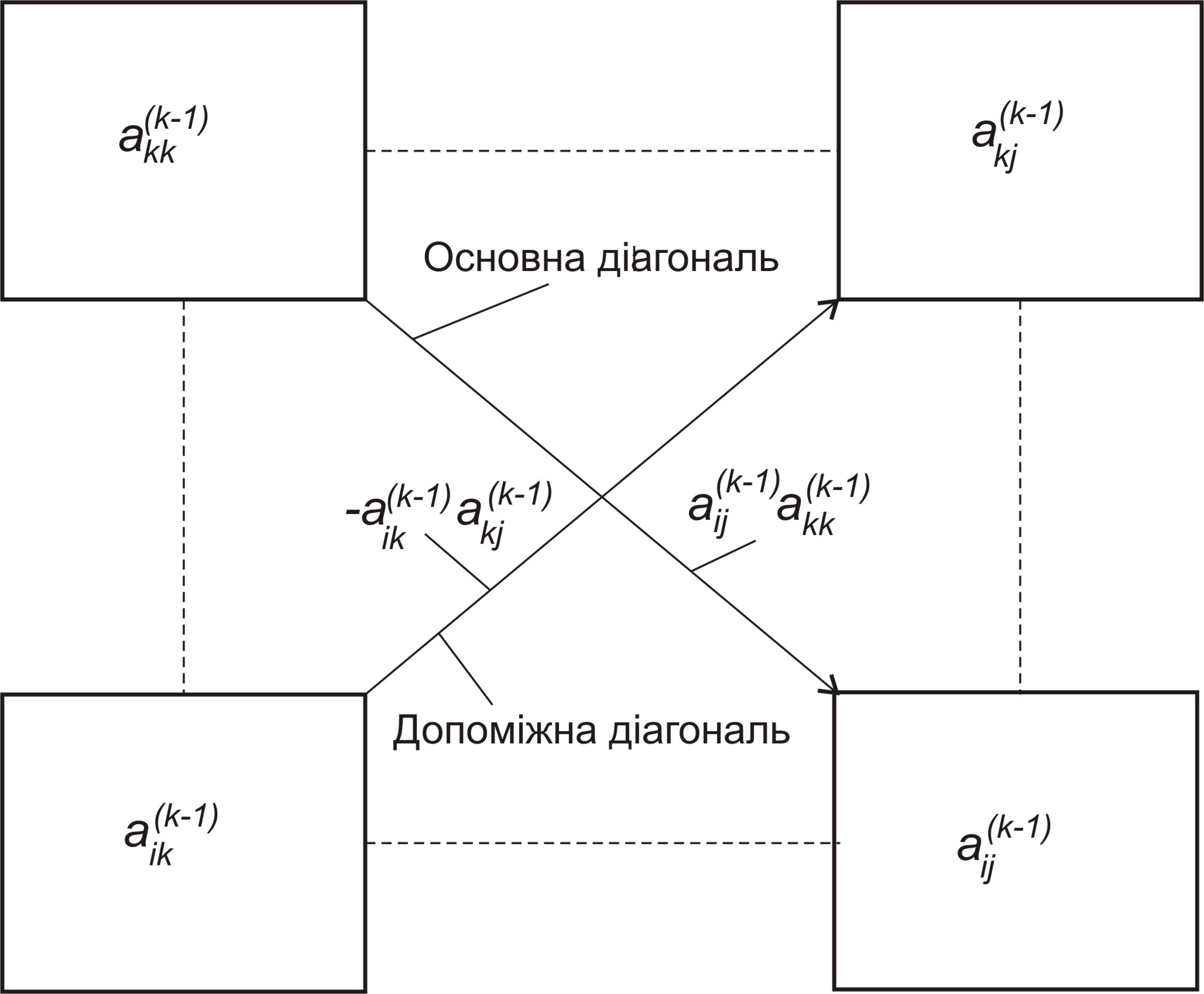
Рисунок 4.1 – Правило прямокутника

Приклад 4.1. Систему лінійних рівнянь

,

,

,

розв’язати методом Гауса.

Перший етап

Перше рівняння системи множимо на (-2) і додаємо його до другого рівняння

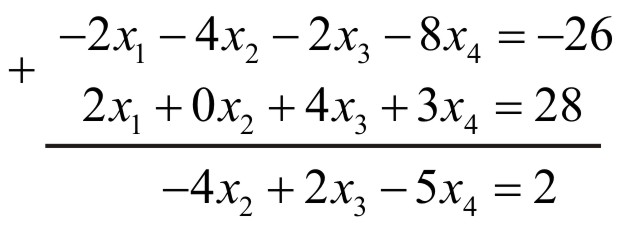
На наступному кроці перше рівняння множимо на (-4) і додаємо його до третього рівняння

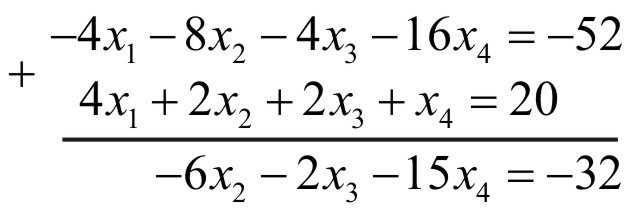
І накінець перше рівняння множимо на 3 і додаємо його до четвертого рівняння

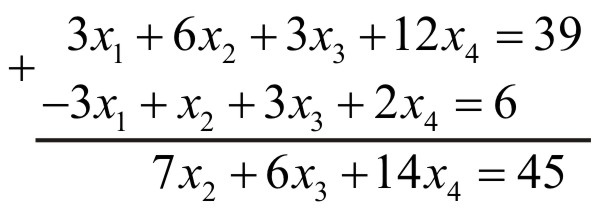
Отже, після першого етапу отримали наступну систему рівнянь:

,

,

,

.

Другий етап

На другому етапі виконуються кроки аналогічні крокам, що виконуються на першому етапі. Тільки вихідною системою рівнянь є система, що отримана після першого етапу обчислень.

Тепер «базовим» рівнянням системи буде її друге рівняння. Це рівняння множимо на і додаємо його до третього рівняння

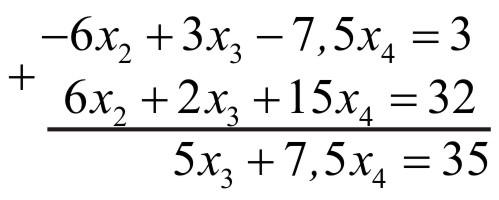
На другому кроці друге рівняння множимо на і додаємо його до четвертого рівняння. у результаті отримаємо

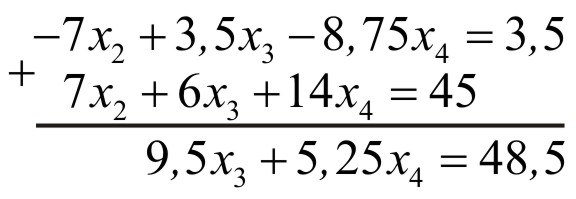
Після закінчення другого етапу обчислень, отримали наступну систему рівнянь:

,

,

,

.

Третій етап

На третьому етапі «базовим» буде третє рівняння системи, яку ми отримали на другому етапі. Це рівняння множимо на і додаємо до четвертого рівняння

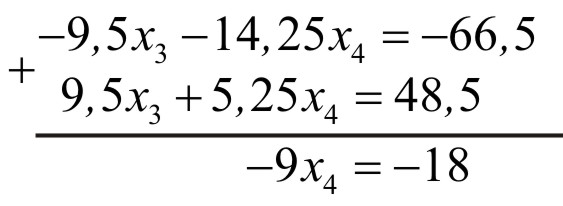
Після трьох етапів обчислень отримали верхню трикутну систему лінійних алгебраїчних рівнянь

,

,

,

,

розв’язок якої починаємо із останнього рівняння. Оскільки воно вміщує тільки одну невідому , то його розв’язком буде . Тепер знайдене значення підставляємо у третє рівняння, яке також вміщує тільки одне невідоме . У результаті розв’язку такого рівняння, матимемо . Аналогічно, підставивши значення і у друге рівняння системи отримаємо значення як її розв’язок - . І на кінець, після підстановки значень , і у перше рівняння системи знаходимо, що .

Наведена нижче процедура SystemEqualizationAgebra¹ знаходить розв’язок системи лінійних алгебраїчних рівнянь, яка подана у матрично-векторній формі (4.2)

SystemEqualizationAgebra^*

А- матриця коефіцієнтів системи розміром nxn

b- вектор вільних членів системи розміром nx1

Х – вектор розв’язків системи розміром nx1

1 n=length(b)

2 Ab=[a b] об’єднання матриць Aі b

Вибір головного елементу для стовпця k

3 for k=1 to n-1

4 for r=k to n

5 ab(r)=Ab(r,k)

6 end for

7 [Y,j]=Max(abs(ab))

Міняємо місцями лінійки k та j

Створюємо нульову матрицю С розміром 1xn+1

8

9

10

11 if AB(k,k)=0

12 then error (‘Матриця А особлива. Cистема немає розв’язку’)

13 end

Процес виключення для стовпця k

14 for p=k to n+1

15 M=Ab(p,k)/Ab(k,k)

16 for r=k to n+1

17 Ab(p,r)=Ab(p,r)-M*Ab(k,r)

18 end for

19 end for

20 end for

Створюємо нульову матрицю As розміром nxn

Створюємо нульовий вектор bs розміром nx1

21 As=Ab

22 bs=b

Обчислення розв’язку методом зворотного ходу

Створюємо нульовий вектор X розміром nx1

23 X(n)=bs(n)/As(n,n)

24 for k=n-1 step -1 to 1

25 s=0

26 for r=k+1 to n

27 s=s+As(k,r)*X(r)

28 end for

29 p(k)=s

30 X(k)=(bs(k)-p(k))/A(k,k)

31 end for

32 return X

У рядках 8 – 9 процедури через і позначені -ий і рядки відповідних матриць.

Процедура SystemEqualizationAgebra побудована так, що на кожному кроці обчислень рівняння у системі (4.1) переставляються таким чином, що у -ому рядку вибирається найбільший за модулем елемент . Це запобігає діленню на нуль і дає змогу зменшити похибки від закруглень.