
Національний авіаційний університет
Інститут екологічної безпеки
ЕК 201(1)
Вітюк Каріна
ЕК201VitLW53.doc
ЕК201VitLW53.mcd
Кафедра прикладної інформатики
Інформатика, основи системології та програмування
Лабораторна робота №3
Київ 2012
1. Тема: дослідження технології обробки масивів екологічних параметрів векторно-матричними перетвореннями з побудовою тривимірних графіків. Розв’язок систем лінійних алгебраїчних рівнянь засобами ППП MathCad.
2. Мета: закріпити знання та вміння із застосування векторно-матричних перетворень з побудовою тривимірних графіків. Навчитись розв’язувати системи лінійних алгебраїчних рівнянь.
3. Короткі теоретичні відомості.
Матричні оператори використовують для здійснення різ-номанітних матричних та векторних перетворень.
Технологія створення векторів та матриць в MathCAD складається з виконання таких дій:
1. Введення імені вектора чи матриці та знака присвоєння.
2. Встановлення розмірів вектора чи матриці.
3. Введення елементів вектора чи матриці в пусті маркери.
Встановлення розмірів вектора чи матриці можна за допо- могою комбінації клавіш Ctrl+M чи на панелі Матрицы и век- торы вибрати команду Матрица или Вектор та викликати ві- кно вставка матриці.
У полі Rows задається необхідна кількість стовпців матри- ці чи вектора, а в полі Columns – необхідна кількість рядків.
Після заповнення необхідно натиснути клавішу Ок.
Елементами векторів та матриць можуть бути:
дійсні та комплексні числа;
функції з числовими значеннями аргументів;
сукупність чисел, функцій, арифметичних операторів та їх обчислення.
4.2 Операції над матрицями
Над матрицями в MathCAD можна виконувати такі дії:
a) додавання до елементів матриці числа: ; z M
b) віднімання від елементів матриці числа: ; z M
c) множення елементів матриці на число: ; z M *
d) ділення елементів матриці на число: ; z M / 58
e) додавання матриць: ; 2 1 MM
f) віднімання матриць: ; 21 MM
g) множення матриць: ; 2*1MM
h) множення елементів матриць: ; 2 *1MM
i) піднесення матриці до степеня: . n M1
Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця) і допускаючий операції (додавання, віднімання, множення та множення на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми. В даній статті вони розглядатися не будуть.
Матриці є корисними для запису даних, що залежать від двох категорій, наприклад: для коефіцієнтів систем лінійних рівнянь та лінійних перетворень.
Операції над векторами
Введення вектора відбувається так само, як і введення мат- риці.
Розглянемо операції над векторами:
1. Транспонування вектора: . T V
2. Сортування вектора: .(Vsort)
3. Зворотне сортування вектора: (Vreverse)
4. Векторизація: . V
5. Норма вектора: . V
6. Визначення числа елементів вектора: (Vlength)
7. Виділення n-го елемента: . n V
8. Повернення номера останнього елемента вектора: (Vlast)
9. Повернення елемента вектора, максимального за значенням: max(V)
10. Повернення елемента вектора, мінімального за значенням: min(V)
11. Повернення дійсної частини елемента вектора: Re(V)
Повернення уявної частини елемента вектора: Im(V)
Матрица - використовують для за-вдання розміру матриці.
Нижний ин-декс - використовують для за-вдання нижнього індек-су.
Инверсия - використовують для об-числення інверсного значення.
Эпитоп - використовують для об-числення визначника матриці або модуля век-тора.
Векторизация - перетворення величини на векторну.
Матричный столбец - використовують для ви-ділення матричного сто-впця з матриц.
Транспонация матрицы - використовують для здійснення операції тра-нспонування матриці.
Переменная диапазона - використовують для за-вдання границь діапазо-ну ранжованої змінної.
Скалярное произведение - використовують для скалярного добутку.
Векторное произведение - використовують для ма-тричного (векторного) добутку.
Векторная сумма - використовують для знаходження векторної суми.
Рисунок - використовують для впровадження рисунка формату .bmp в доку-мент програми.
Геометричний вектор — у фізиці і математиці - величина, яка характеризується числовим значенням і напрямком. У фізиці існує чимало важливих величин, котрі є векторами, наприклад сила, положення, швидкість, прискорення, кутовий момент, імпульс, напруженість електричного і магнітного полів. Їх можна протиставити іншим величинам, таким, як маса, об’єм, тиск, температура та густина, які можна описати звичайним числом, їх називають «скалярами».
Вектор в програмуванні - одномірний масив.
Вектори і матриці розглядаються у програмі MathCad як одновимірні і двовимірні масиви даних. Число рядків і стовпців матриці задається в діалоговому вікні Insert Matrix (Вставка матриці), що відкривають командою Insert> Matrix (Вставка> Матриця). Вектор задається як матриця, що має один стовпець.
Після клацання на кнопці ОК у формулу вставляється матриця, що містить замість елементів заповнювачі. Замість кожного заповнювача треба вставити число, змінну або вираз.
Колекція тривимірних графіків — справжнє диво, яке Mathcad дарил користувачеві. За лічені секунди ви можете створити прекрасну презентацію результатів своїх розрахунків. Рамки даної книги не дозволяють описати техніку їх створення і форматування детально, тому ми обмежимося лише ввідними зауваженнями і простими прикладами, які допоможуть орієнтуватися в подальшому матеріалі.
Щоб створити тривимірний графік, потрібно натиснути кнопку із зображенням будь-якого з типів тривимірних графіків на панелі інструментів Graph (Графік). В результаті з'явиться порожня область графіка з трьома осями і єдиним местозаполнітелем в нижньому лівому кутку. У цей местозаполнітель слід ввести або ім'я z функції z(x,y) два змінних для швидкої побудови тривимірного графіка , або ім'я матричної змінної z яка задасть розподіл даних zx,y на плоскості XY. Ще раз відзначимо, що для отримання графіків (і цих, і подальших) не потрібний ніякого тексту, окрім відповідного лістингу і введення імені відповідної функції або матриці в местозаполнітель.
Окрім тривимірних графіків поверхні, натиснення відповідних кнопок на панелі Graph (Графік) приводить до створення графіка ліній рівня , тривимірної гістограми, тривимірного розподілу крапок або векторного поля.
Для побудови поверхні в панелі графіків є кнопка По- верхностный график з панелі Графики.
При ініціалізації цієї кнопки на екран виводиться заготовка об’ємного графіка поверхні, що має вигляд прямокутника, в лі- вому нижньому куті якого знаходиться чорний квадратик. На його місце треба помістити ім’я матриці чи вектор, які потім бу- дуть зображені у вигляді об’ємного графіка.
Для побудови графіка функції двох змінних перед його за- готовкою задається додаткова інформація:
визначається функція
вводиться індексація вузлів сітки
формуються вектори значень аргументів, що відпо- відають вузлам сітки
обчислюється матриця значень функції, аргументи яких відповідають вузлам сітки
Ця інформація розміщується перед полем графіка. Побудо- ваний відповідно до заданої матриці графік функції двох змін- них має вигляд просторової сітки. Графік побудований на рис. 14.10.
Цей графік можна редагувати за допомогою подвійного клацання мишкою по графіку, після чого з’явиться вікно, зобра- жене на рис.
О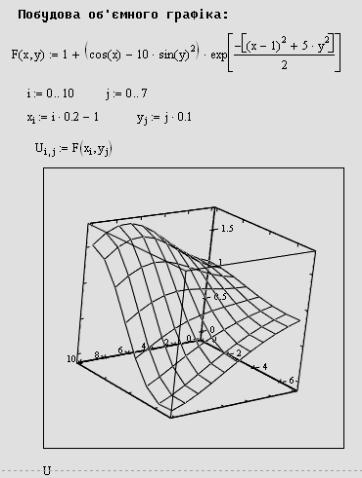 б’ємний
графік
б’ємний
графік
Контрольні запитання
1. Що таке матриця?
2. Що таке вектор?
3.Що являє собою формат матриці?
4.Що таке векторні матричні операції?
5. Побудова тривимірного графіку.
6. Форматування тривимірного графіку.
7. Система алгебраїчних рівнянь.
8.Операції над матрицями.
9. Для чого використовується кнопка MatrixColumn?
10. Як задати число рядків та стовпців матриці?
4. Хід роботи.
4.1. Постановка завдання. Сформувати двовимірний масив середньомісячних значень шкідливої речовини за варіантом щоквартально протягом року. Знайти середнє значення, накопичення, екстремальні значення за третій квартал. Побудувати тривимірні графіки двох типів а також стовпчикову діаграму. Виконати їх форматування. Розв’язати систему лінійних алгебраїчних рівнянь.
4.2. Інформаційна модель.
1) h = Bl ГДК = 3.0 мг/м3
|
I |
II кв |
III кв |
IV кв |
|
|
3.3 |
3.25 |
3.35 |
3.7 |
|
PopZn = |
3.0 |
3.2 |
3.45 |
3.6 |
|
|
3.2 |
3.4 |
3.5 |
3.1 |
|
|
|
|
|
|
|
km = 3
VitnakBl = VitBl<3>
VitszBl =VitnakBl /km
maxBl (VitBl <3>)
minBl (VitBl <3>)
2)
|
I кв |
II кв |
III кв |
IV кв |
|
3.3 |
3.25 |
3.35 |
3.7 |
PopZn = |
3.0 |
3.2 |
3.45 |
3.6 |
|
3.2 |
3.4 |
3.5 |
3.1 |
KBl=
-
I кв
II кв
III кв
3.3
3.25
3.35
3.0
3.2
3.45
3.2
3.4
3.5
OBl=
IV кв |
3.7 |
3.6 |
3.1 |
VitBl = lsolve (KBl,OBl)
4.3. Готове програмне забезпечення. MS Word 2010, PTC MathCad.
4.4. Алгоритмічно-програмна модель:
Початок
Схему розробила студентка ІЕБ 201 Вітюк Каріна
Двовимірний масив
Схему розробив студент 201 групи ІЕБ
km = 3
VitnakBl= А
VitszBl =В
А= VitBl<3>
В=VitnakBl /km
maxBl
minBl
KBl
1
1
OBl
VitBl = T
T = lsolve ( KBl, OBl )
Вивід результату
VitnakBl VitszBl,maxBl, minBl
Кінець
1. Векторно-матричні перетворення

![]()
![]()
![]()
![]()
![]()
2. Розв язок системи лінійно-алгебраїчних рівнянь
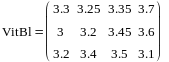


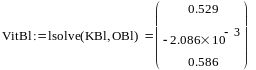

Стовпчикова діаграма
4.5. Результат.
VitnakBl =10.4
VitszBl = 3.467
maxBl = 3.7
minBl = 3.1
2)

4.6. Аналіз результату: роботу було проведено вірно, результат правильний.
5. Висновок: закріпила знання та вміння із застосування векторно матричних перетворень з побудовою тривимірних графіків. Навчилась розв’язувати системи лінійних алгебраїчних рівнянь.

 кв
кв