
Послідовність роботи на прикладі параметричної оптимізації сар
1 Побудувати модель об’єкту оптимізації у вікні Simulink, наприклад
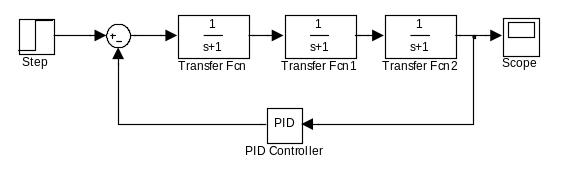
2 Задати відомі параметри для блоків моделі. У вікні блоку регулятора ввести замість значень параметрів регулятора їх ідентифікатори, наприклад, kr, ki, kd.
3 Задати початкові значення вектора параметрів оптимізації (параметрів регулятора) та з командного рядка (чи m-файлу) передати їх в робочий простір Matlab, наприклад:
Kr=1; ki=0.5, kd=0.
4 Запустити процес моделювання та, при необхідності, у вікні Simulation/ Simulation parameters змінити час початку і кінця перехідного процесу.
3 Знайти іконку блоку NCD Blockset у переліку вікна Simulink Library Browser, відкрити її та перетягнути мишкою блок NCD Outport у вікно моделі Simulink.
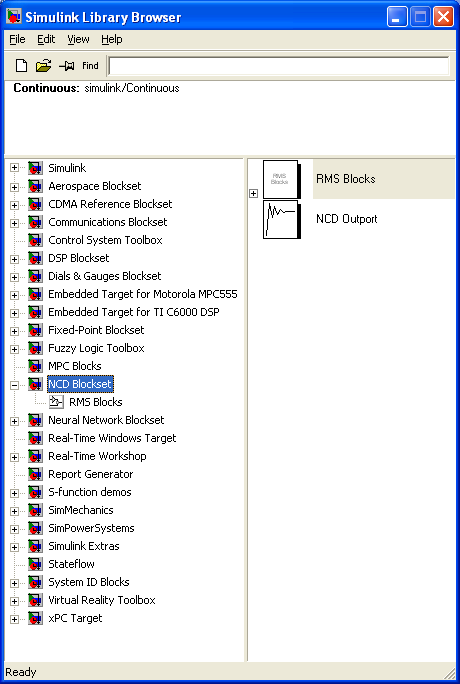

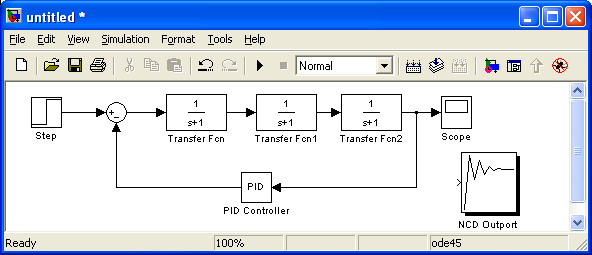
5 Підєднати вихід моделі до входу блоку
6 У вікні Optimization Parameters, в полі Tunable Variables ввести ідентифікатори коефіцієнтів регулятора.
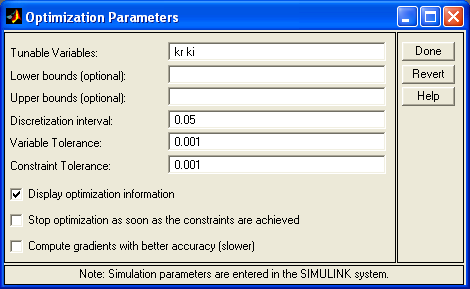
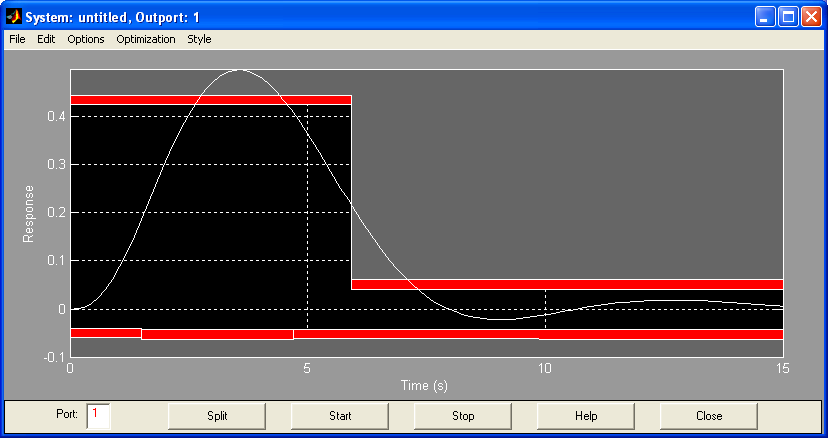
7 Відкрити вікно блоку NCD та виконати команду Options\ Initial response (Ctrl+I).

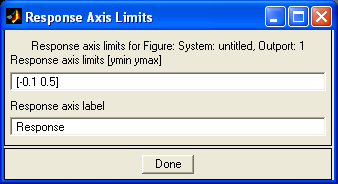
8 За отриманим графіком перехідного процесу мишкою зредагувати допустимі межі перехідного процесу та змінити масштаб по вихідній величині Options\Y-Axis
9 Запустити на виконання процедуру оптимізації Optimization\ Start (Ctrl+S)
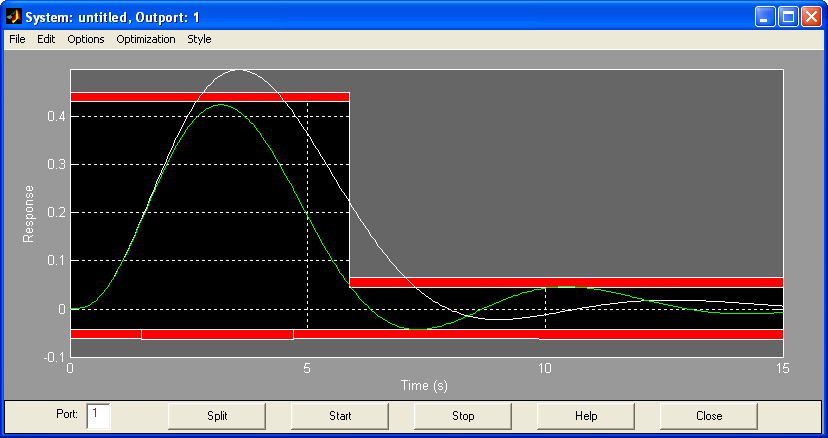
10 У вікні Matlab зчитати параметри оптимізації, які забезпечують задану якість перехідного процесу
>> kr
kr = 1.5707
>> ki
ki = 0.6986
ВАРІАНТИ ЗАВДАНЬ
1 Задано експериментальні значення кривої розгону лінійного об’єкту керування третього порядку з функцією передачі
![]()
на вхідний сигнал U= 1:
Коефіцієнт передачі К=2 відомий з точністю 10 %
t = [0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 40 42 44 46 48 50]
y(t) = [0 0.53 1.76 2.45 2.4 2.1 1.88 1.89 1.98 2.0 2.03 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0]
Виконати параметричну ідентифікацію об’єкту в середовищі Matlab-Simulink із застосуванням блоку NCD
2 Задано експериментальні значення кривої розгону лінійного об”єкту керування порядку з функцією передачі
![]()
на вхідний сигнал U= 2:
t = [0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 40 42 44 46 48 50]
y(t) = [0 0.53 1.76 2.45 2.4 2.1 1.88 1.89 1.98 2.0 2.03 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0]
Виконати параметричну ідентифікацію об’єкту в середовищі Matlab-Simulink із застосуванням блоку NCD.
3 Задано експериментальні значення реакції лінійної системи керування на стрибкоподібне збурення:
t = 0 1.2 1.9 2.7 3.5 4.3 5.9 6.7 9.1 12.3 21.1 26.7 30.7 40.0 50.0
y(t)=0 0.6 1.1 1.6 1.9 1.9 1.7 1.5 1.0 0.65 0.23 0.12 0.07 0.02 0.0
Задані також параметри ПІ-регулятора та функція передачі об”єкту керування:
кр=3
кі=0.5
![]()
Виконати параметричну оптимізацію об”єкту керування в середовищі Matlab-Simulink із застосуванням блоку NCD (побудувати модель у вікні Simulink, задати параметри моделювання та параметри блоку NCD).
4 Задано експериментальні значення кривої розгону лінійного об”єкту керування третього порядку з функцією передачі
![]()
на вхідний сигнал U= 1:
t = [0 0.9 1.2509 1.7 2.8 3.5 4.5 5.4 6.0 7.0 10.4 15 20]
y(t) = [0 0.5 0.7672 1.1 1.6 1.8 2.0 2.1 2.2 2.2 2.1 2.0 2.0]
Поставити та розв'язати задачу безумовної параметричної оптимізації об”єкту для квадратичного інтегрального критерію на інтервалі 100 с (визначити параметри моделі – коефіцієнти функції передачі a1, a2, a3, b1).
Задачу розв'язати в середовищі Matlab із застосуванням функцій оптимізації бібліотеки Optimization Toolbox.
1 Задано об"єкт керування – послідовне з"єднання трьох аперіодичних ланок:
![]() ,
,
![]() ,
,
![]()
Синтезувати систему керування з ПІ – регулятором, переміщення регулюючого органу якої не повинно перевищувати 0.2.
Параметричну оптимізацію системи керування виконати в середовищі Matlab-Simulink із застосуванням блоку NCD (побудувати модель у вікні Simulink, задати параметри моделювання та параметри блоків NCD).
1 Задано об"єкт керування – послідовне з"єднання трьох аперіодичних ланок:
, ,
Синтезувати систему керування з ПІ – регулятором. Обмеження на параметри регулятора:
Ті > 0.5; Kp < 10
Параметричну оптимізацію системи керування виконати в середовищі Matlab-Simulink із застосуванням блоку NCD (побудувати модель у вікні Simulink, задати параметри моделювання та параметри блоку NCD).
1 Задано експериментальні значення кривої розгону трьох ємнісного аперіодичного лінійного об”єкту керування на вхідний сигнал U= 2:
t = [0 0.69 1.1 1.6 2.35 3.2 4.0 4.8 5.6 7.2 8.8 11.2 17.6 20.8 30.4 40 50]
y(t) = [0 0.02 0.06 0.15 0.35 0.6 0.9 1.3 1.6 2.2 2.6 3.1 3.7 3.9 4.0 4.0 4.0]
Поставити та розв'язати задачу безумовної параметричної оптимізації об”єкту (визначити параметри моделі – коефіцієнт підсилення та сталі часу аперіодичних ланок).
Задачу розв'язати в середовищі Matlab із застосуванням функцій оптимізації бібліотеки Optimization Toolbox.
1 Задано об"єкт керування – послідовне з"єднання трьох аперіодичних ланок:
, ,
Параметри функцій передачі відомі з точністю 20 %.
Визначити параметри настроювання ПІ – регулятора, які б задовільняли заданий перехідний процес.
Параметричну оптимізацію системи керування виконати в середовищі Matlab-Simulink із застосуванням блоку NCD (побудувати модель у вікні Simulink, задати параметри моделювання та параметри блоку NCD).
1 Задано експериментальні значення реакції лінійної системи керування на стрибкоподібне збурення:
t = 0 1.2 1.9 2.7 3.5 4.3 5.9 6.7 9.1 12.3 21.1 26.7 30.7 40.0 50.0
y(t)=0 0.6 1.1 1.6 1.9 1.9 1.7 1.5 1.0 0.65 0.23 0.12 0.07 0.02 0.0
Задані також параметри ПІ-регулятора та функція передачі об”єкту керування:
Кр=3
Кі=0.5
Параметр настроювання Кі відомий з точністю 20%.
Виконати параметричну оптимізацію об”єкту керування в середовищі Matlab-Simulink із застосуванням блоку NCD (побудувати модель у вікні Simulink, задати параметри моделювання та параметри блоку NCD).
1 Задано експериментальні значення кривої розгону лінійного об”єкту керування третього порядку з функцією передачі

на вхідний сигнал U= 1:
t = [0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 40 42 44 46 48 50]
y(t) = [0 0.53 1.76 2.45 2.4 2.1 1.88 1.89 1.98 2.0 2.03 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0]
Поставити та розв'язати задачу безумовної параметричної оптимізації об”єкту (визначити параметри моделі – коефіцієнти функції передачі a1, a2, a3 , b1).
Задачу розв'язати в середовищі Matlab із застосуванням функцій оптимізації бібліотеки Optimization Toolbox
1 Задано експериментальні значення кривої розгону лінійного об”єкту керування порядку з функцією передачі

на вхідний сигнал U= 2:
t = [0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 40 42 44 46 48 50]
y(t) = [0 0.53 1.76 2.45 2.4 2.1 1.88 1.89 1.98 2.0 2.03 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0]
Виконати параметричну оптимізацію об”єкту в середовищі Matlab-Simulink із застосуванням блоку NCD (побудувати модель у вікні Simulink, задати параметри моделювання та параметри блоку NCD).
1 Задано об"єкт керування – послідовне з"єднання трьох аперіодичних ланок:
, ,
Синтезувати систему керування з ПІ – регулятором, переміщення регулюючого органу якої не повинно перевищувати 0.2.
Параметричну оптимізацію системи керування виконати в середовищі Matlab-Simulink із застосуванням блоку NCD (побудувати модель у вікні Simulink, задати параметри моделювання та параметри блоків NCD).
1 Задано експериментальні значення реакції лінійної системи керування на стрибкоподібне збурення:
t = 0 1.2 1.9 2.7 3.5 4.3 5.9 6.7 9.1 12.3 21.1 26.7 30.7 40.0 50.0
y(t)=0 0.6 1.1 1.6 1.9 1.9 1.7 1.5 1.0 0.65 0.23 0.12 0.07 0.02 0.0
Задані також параметри ПІ-регулятора та функція передачі об”єкту керування:
Кр=3
Кі=0.5
Параметр настроювання Кі відомий з точністю 20%.
Виконати параметричну оптимізацію об”єкту керування в середовищі Matlab-Simulink із застосуванням блоку NCD (побудувати модель у вікні Simulink, задати параметри моделювання та параметри блоку NCD).
1 Задано експериментальні значення реакції лінійної системи керування на стрибкоподібне збурення:
t = 0 1.2 1.9 2.7 3.5 4.3 5.9 6.7 9.1 12.3 21.1 26.7 30.7 40.0 50.0
y(t)=0 0.6 1.1 1.6 1.9 1.9 1.7 1.5 1.0 0.65 0.23 0.12 0.07 0.02 0.0
Задані також параметри ПІ-регулятора та функція передачі об”єкту керування:
Кр=3
Кі=0.5
Параметр настроювання Кі відомий з точністю 20%.
Виконати параметричну оптимізацію об”єкту керування в середовищі Matlab-Simulink із застосуванням блоку NCD (побудувати модель у вікні Simulink, задати параметри моделювання та параметри блоку NCD).
1 Задано експериментальні значення кривої розгону лінійного об”єкту керування третього порядку з функцією передачі
на вхідний сигнал U= 1:
t = [0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 40 42 44 46 48 50]
y(t) = [0 0.53 1.76 2.45 2.4 2.1 1.88 1.89 1.98 2.0 2.03 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0]
Поставити та розв'язати задачу безумовної параметричної оптимізації об”єкту (визначити параметри моделі – коефіцієнти функції передачі a1, a2, a3 , b1).
Задачу розв'язати в середовищі Matlab із застосуванням функцій оптимізації бібліотеки Optimization Toolbox.
