Как изменяется вид функции распределения Ферми-Дирака при нагреве кристалла от абсолютного нуля до некоторой температуры т.
Вид
функции Ферми-Дирака для двух различных
температур показан схематически на
рис. 3.13. Изменение характера распределения
электронов по состояниям связано с
тепловым возбуждением электронов. При
этом часть электронов переходит в
состояния с энергиями, большей энергии
Ферми. Соответственно часть состояний
ниже уровня Ферми оказывается свободной.
В результате функция f(E) "размыта"
вблизи энергии Ферми. Тепловому
возбуждению подвергается незначительная
часть электронов, находящихся вблизи
уровня Ферми. Функция Ферми-Дирака
заметно отличается от вида, который она
имела при абсолютном нуле, лишь при
.
Величина "размытия" пропорциональна
температуре (рис. 3.13). Чем выше температура,
тем более существенному изменению
подвергается функция распределения.
Выразите темературные зависимости концентрации электронов в зоне проводимости и дырок в валентной зоне собственного полупроводника.
Для
собственного полупроводника концетрации
электронов и дырок имеют вид
(3.8а)
.
Где Nc называют эффективной плотностью состояний в зоне проводимости, а Nv - эффективная плотность состояний в валентной зоне.
Выразите темературные зависимости концентрации электронов в зоне проводимости и дырок в валентной зоне примесного полупроводника.
Для примесного полупроводника n-типа проводимости она выражается соотношением
,
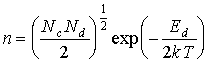(3.6а)
где
NC
=
.
Концентрация дырок
,
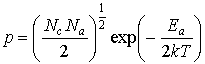(3.7а)
где эффективная плотность состояний в валентной зоне
NV
=
.
Опишите понятие законп действующих масс.
Для полупроводников справедливо еще одно интересное соотношение
(3.9а)
Это соотношение (3.9а) называется законом действующих масс. При выводе этого закона использовано предположение о том, что степень заполнения энергетических уровней носителями заряда много меньше единицы. Такой газ носителей называется невырожденным, а полупроводники – невырожденными.
Другими словами, закон действующих масс выполняется для любого невырожденного полу-проводника независимо от роли примесей, т.е. в любом невырожденном полупроводнике увеличение концентрации носителей одного знака приводит к уменьшению концентрации носителей противоположного знака. Следует отметить также, что произведение электронной и дырочной концентраций не зависит от положения уровня Ферми.
Опишите положение уровня Ферми в собственном полупроводнике.
. (3.11)
Если
эффективные массы электронов и дырок
равны, т.е.
уровень Ферми собственного полупроводника
при любой температуре располагается
посередине запрещенной зоны.
Опишите положение уровня Ферми в примесном полупроводнике р-типа.
Расчеты показывают, что при низких температурах, когда электроны в зоне проводимости появляются в основном за счет переходов с примесных уровней, а концентрация дырок близка к нулю, температурная зависимость энергии Ферми имеет вид
(3.13а)
(3.13б)
Из уравнений (3.13) следует, что при абсолютном нуле температуры энергия Ферми донорного полупроводника находится строго посередине между дном зоны проводимости и донорными уровнями Температурная зависимость положения уровня Ферми определя-ется третьим членом в уравнений (3.13), который меняет знак с изменением температуры. Поэтому уровень Ферми у донорного полупроводника с повышением темпера-туры сначала смещается к зоне проводимости, а затем - к валентной зоне (рис. 3.15а). У акцепторного полупроводника все наоборот (рис. 3.15б).
Рис.
3.15.
Температурные зависмости уровня Ферми
для полупроводника электронного (а) и
дырочного (б) типа проводимости.
Опишите положение уровня Ферми в собственном полупроводнике n-типа.
См.предыдущий вопрос.
Запишите и объясните соотношение для проводимости металлического кристалла.
Построим мысленно в объеме проводника цилиндр с основанием, равным единице площади, и образующей, равной скорости дрейфа vдр и направленной вдоль дрейфа (рис. 3.16). Все электроны, заключенные в этом цилиндре, в течение 1 с пройдут через его основание и образуют ток с плотностью
,
(3.14)
где n - концентрация электронов проводимости.
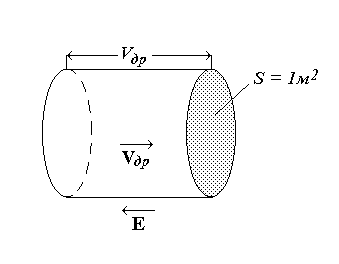
Рис. 3.16. К расчету удельной электропроводности металла
Выражение (3.14) имеет форму закона Ома, где электропроводность электронного газа есть коэффициент пропорциональности между плотностью тока j и напряженностью электрического поля Е, т.е. j =nЕ. Здесь удельная проводимость электронного проводника можно выразить следующим образом:
.
Чтот такое подвижность носителей заряда?
Подвижностью называют величину, равную отношению скорости дрейфа носителя к напряженности электрического поля. Для электронов подвижность
,
(3.16)
для дырок
,
(3.17)
где p
и
-
время релаксации и эффективная масса
дырки соответственно. Таким образом,
подвижность - это дрейфовая скорость,
приобретенная носителями заряда в
электрическом поле единичной напряженности.
Опишите качественно поведение температурной зависимости удельного соспротивления металлов. Правило Матиссена.
Электросопротивление большинства металлов обусловлено рассеянием электронов на различных видах нарушений регулярной кристаллической структуры решетки - тепловых колебаниях ионов кристаллической решетки (фононов) и статических дефектов кристаллической решетки.
В соответствии с этим и электросопротивление реального металла, в котором в той или иной степени присутствуют все виды рассеяния электронов проводимости, приближенно представляют в виде двух слагаемых
,
(3.18)
здесь о - часть удельного электросопротивления, обусловленная рассеянием электронов на статических дефектах, (T) - часть удельного электросопротивления, обусловленная рассеянием на фононах.
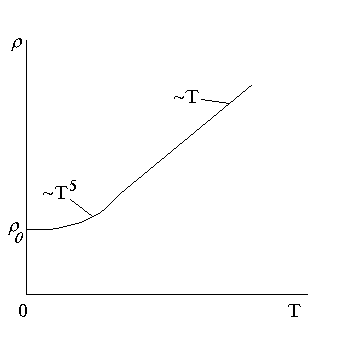
Рис. 3.17. Зависимость удельного электросопротивления металла от температуры
При очень низких температурах, когда влиянием тепловых колебаний на рассеяние электронов можно пренебречь, сопротивление металлов практически перестает зависеть от температуры (рис. 3.17). Предельное значение о, к которому стремится сопротивление металлов по мере понижения температуры к абсолютному нулю, называется остаточным сопротивлением.