Как возникают и как называются носители заряда, определяющие электропроводность в собственных (бездефектных) полупроводниковых кристаллах. Изобразите схему генерации таких носителей.
Для того чтобы по собственному (бездефектному) кристаллу пошел электрический ток (то есть кристалл обладал бы проводимостью), необходимо «освободить» хотя бы часть электронов, то есть «вырвать» их из связей. Уход электрона из связи оставляет на его месте «электронную вакансию» или дырку. Таким образом, в кристалле возникают два типа носителей – отрицательные электроны и положительные дырки.
Как видно из рис. 3.9, разрыв связи в полупроводнике означает переброс электрона из валентной зоны (EV) в зону проводимости (EC) с одновременным перебросом дырки в валентную зону. Этот процесс называется генерацией носителей заряда.
Рис. 3.9. Зонная схема образования электронов и дырок в бездефектном полупроводнике
Поскольку бездефектный полупроводник принято называть собственным, то и генерируемые электронно-дырочные пары называются собственными носителями.
Опишите схематически энергетический спектр носителей заряда в полупроводнике электронного типа. При каком типе примесей такой полупроводник формируется?
При замене в узле кристаллической решетке атома Si на атом примеси с большей валентностью, называемый донорной примесью (например, на элемент V группы - P, As, Sb), в кристалле появляется лишний, не спаренный электрон и положительно заряженный примесный атом. Это означает, что на зонной схеме полупроводника в запрещенной зоне вблизи края С-зоны появляется донорный уровень Ed (рис. 3.10б), расстояние которого от края С-зоны называется энергией ионизации донора. Образовавшийся таким образом не спаренный электрон очень слабо связан с ионом примеси и легко может от него оторваться, или другими словами, каждый электрон уйдет с примесного уровня в С-зону
Опишите схематически энергетический спектр ностелей заряда в полупроводнике дырочного типа. При каком типе примесей такой полупроводник формируется?
При замене в узле кристаллической решетке атома Si на атом с меньшей валентностью, называемый акцепторной примесью (например, на элемент III группы - B, Al, Ga), в кристалле появляется отрицательно заряженный примесный ион и слабо связанная с ним электронная вакансия (дырка) - рис. 3.11а. Это означает, что на зонной схеме полупроводника в запрещенной зоне вблизи края V-зоны появляется акцепторный уровень Eа (рис. 3.11б), расстояние которого от края V-зоны называется энергией ионизации акцептора. В результате такой полупроводник называется полупроводником p-типа проводимости (с дырочной проводимостью).
Покажите графически и объясните вид функции распределения Ферми-Дирака при абсолютном нуле и при нагреве кристалла.
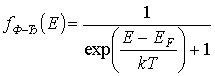
Как нетрудно видеть из формулы, для любой энергии частицы, большей энергии Ферми, экспонента в знаменателе стремится к бесконечности при Т 0 К, следовательно f(Е) стремится к нулю. Это значит, что все энергетические состояния с Е > EF совершенно свободны при абсолютном нуле. Если Е < EF при Т = 0 К, f(E) стремится к единице. Это значит, что все квантовые состояния с энергией, меньше энергии Ферми, полностью заняты электронами.
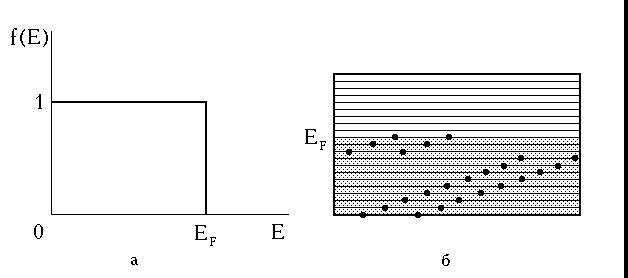
Если Т ≠ 0К, то при энергии частицы, равной энергии Ферми, функция распределения Ферми-Дирака равна 1/2. Это значит, что при любой температуре, отличающейся от абсо-лютного нуля, уровень Ферми заполнен наполовину
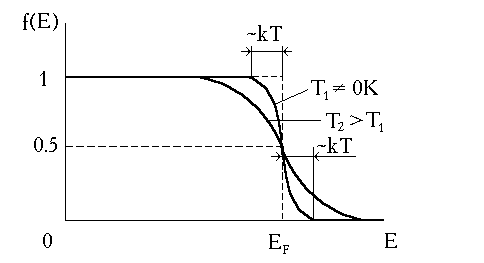
Рис. 3.13. Функция распределения Ферми-Дирака при Т > 0K