- •Ю.И. Самоходов, а.Ю. Абызгильдин, м.М. Абдуллин, п.А. Федоров проекции с числовыми отметками в инженерно-геологической графике
- •Часть II
- •Ю.И. Самоходов, а.Ю. Абызгильдин, м.М. Абдуллин, п.А. Федоров
- •Введение
- •Основные термины и определения
- •Дополнительные обозначения, используемые в проекциях с числовыми отметками
- •Топографические поверхности § 1.1 Элементы топографической поверхности
- •§ 1.2 Позиционные задачи на топографических поверхностях
- •§ 1.3 Линия наибольшего ската топографической поверхности
- •§ 1.4 Линия заданного уклона топографической поверхности
- •§ 1.5 Пересечение прямой линии с топографической поверхностью
- •§ 1.6 Пересечение наклонной плоскости с топографической поверхностью
- •§ 1.7 Взаимное пересечение двух топографических поверхностей
- •§ 1.8 Построение линии пересечения конической поверхности с топографической поверхностью
- •§ 1.9 Линия пересечения поверхности одинакового ската с топографической поверхностью
- •§ 1.10 Пересечение пространственной кривой к с отметками точек а10 и в11 с топографической поверхностью
- •§ 1.11 Построение аксонометрической проекции (изометрии) топографической поверхности координатным способом
- •§ 1.12 Построение аксонометрической проекции (изометрии) топографической поверхности путём перемещения изометрического плана по вертикальной линии
- •Определение элементов залегания пласта § 2.1 Определение элементов залегания пластов с помощью горного компаса, по данным бурения и по линии выхода пластов* на поверхность
- •§ 2.2 Определение элементов залегания нефтяного пласта по данным бурения, с использованием методов начертательной геометрии*
- •§ 2.3 Определение элементов залегания по выходу пласта на поверхность
- •§ 2.4 Определение элементов залегания пласта по двум видимым наклонам
- •§ 2.5 Определение истинной мощности пласта при наклонном залегании
- •§ 2.6 Использование методов начертательной геометрии для решения инженерно-геологических задач**
- •Пример графического определения контура продуктивного пласта и мощности его вскрытия наклонно-направленной скважиной § 3.1 Исходные данные к заданию
- •§ 3.2 Правила и последовательность выполнения задания
- •Построение положения скважины
- •Построение геологического профиля
- •Библиографический список
- •Приложение а (справочное) Оформление горно-геологических чертежей
- •Приложение б (справочное)
- •Приложение в (обязательное) Масштабы
- •Численный масштаб
- •Линейный масштаб
- •Поперечный масштаб
- •Приложение г (обязательное) Линии
- •Приложение д (справочное) Основные надписи
- •Приложение е (рекомендованное) Шрифты чертежные
- •План автомобильной дороги топографический
- •Обозначение графических материалов и горных пород в сечениях и правило их нанесения на чертежах
- •Специальные и прочие условные обозначения на геологических и топографических картах и горных чертежах
- •Оглавление
- •Часть II
- •450062, Г. Уфа, ул. Космонавтов, 1. Для заметок
§ 1.2 Позиционные задачи на топографических поверхностях
При решении различных задач на топографической поверхности считают, что прямая линия, соединяющая две точки смежных горизонталей (рисунок 1.5), например прямая АВ или CD, всеми своими точками расположена на поверхности. Чем меньше разность отметок горизонталей, тем меньше погрешность в этом допущении.
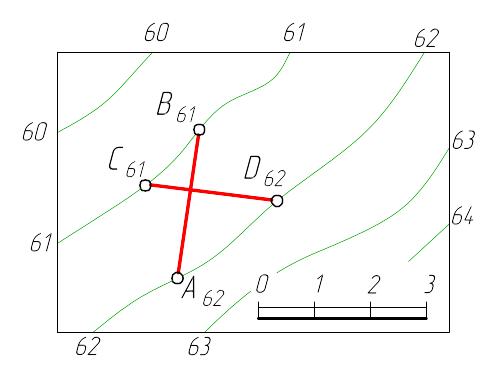
Рисунок 1.5
§ 1.3 Линия наибольшего ската топографической поверхности
Линия наибольшего ската топографической поверхности представляет собой линию, которая в данной точке поверхности имеет наибольший уклон. Это пространственная кривая линия, чаще всего - ломаная. Линия наибольшего ската строится таким образом: ножку циркуля установить в точку А (А принадлежит горизонтали 6-6), проводим дугу (рисунок 1.6), которая касается следующей горизонтали с меньшей отметкой. Затем из полученной точки повторяем построение к другим горизонталям и соединяем полученные точки.
Если рельеф местности сложный и горизонтали сильно отличаются по своему направлению, то необходимо на данном участке увеличить их количество.
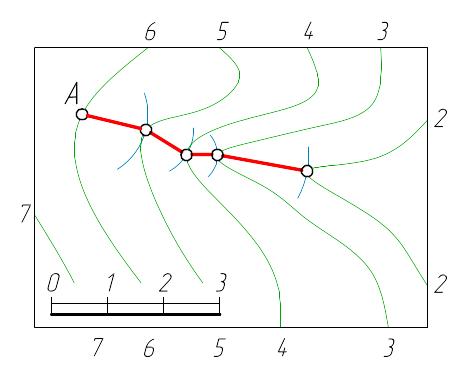
Рисунок 1.6
§ 1.4 Линия заданного уклона топографической поверхности
Линия заданного уклона поверхности представляет собой линию, принадлежащую поверхности и имеющую одинаковый уклон в любой точке на всем её протяжении. Интервалы такой линии одинаковы в любом её месте.
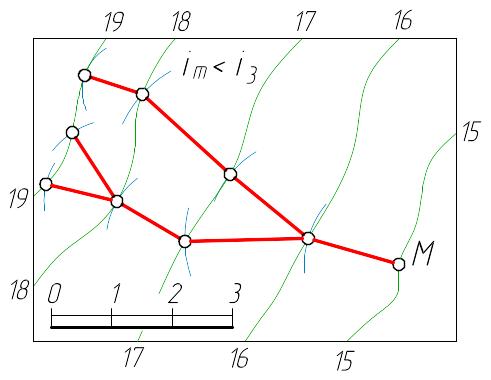
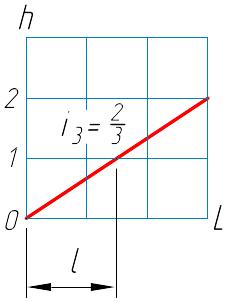
На рисунке 1.7 показано построение линии заданного уклона из точки М. Радиус дуги равен интервалу уклона i (или заданного угла ).
Задача имеет несколько решений. Для однозначного решения должны быть дополнительные условия. Допустим, линия должна идти в заданном направлении. Если дуга (интервал) заданного уклона не пересекает соседние горизонтали, значит, уклон местности im меньше i3.
|
|
а) |
б) |
Рисунок 1.7
§ 1.5 Пересечение прямой линии с топографической поверхностью
Построение точек пересечения прямой линии с топографической поверхностью в проекциях с числовыми отметками основано на использовании способа вспомогательных секущих плоскостей или же с помощью построения профиля поверхности.
Рассмотрим оба этих способа. Задана прямая АВ и топографическая поверхность своими горизонталями. Определить точку встречи прямой и поверхности.
Первый способ (рисунок 1.8): через прямую АВ проведём вспомогательную секущую плоскость общего положения. Для этого проградуируем прямую АВ, проведём через данные точки градуировки горизонтали, параллельные между собой в любом направлении, но таким образом, чтобы одноименные горизонтали плоскости и поверхности пересеклись в пределах чертежа. Строим линию пересечения поверхности со вспомогательной плоскостью. Для этого отметим точки пересечения С и D – пересечения горизонтали плоскости и поверхности, имеющие одинаковые отметки. Полученная плавная кривая линия является линией пересечения поверхности плоскостью.
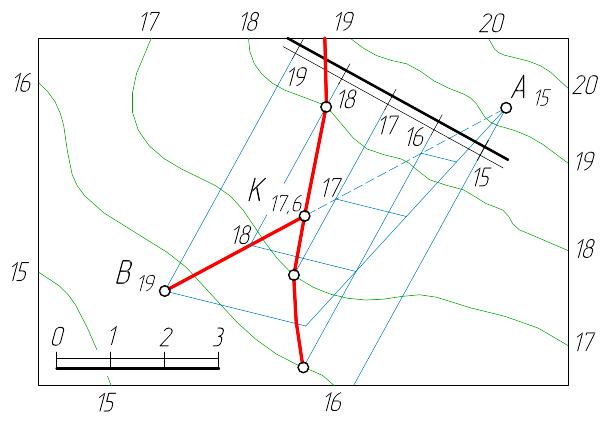
Рисунок 1.8
Точкой встречи прямой АВ с поверхностью будет точка К, полученная пересечением линии CD с прямой АВ (по свойству инцидентности).
Второй способ: через прямую АВ (рисунок 1.9, а, б) проводим проецирующую плоскость Qi и строим профиль топографической поверхности (направлением профилирования будет прямая АВ). Через точки пересечения проекции следа плоскости Qi с горизонталями поверхности на плане откладываем в масштабе чертежа по перпендикулярам к проекции прямой высотные отметки точек, равные отметкам горизонталей. Соединив полученные точки плавной кривой, получим профиль поверхности. Таким же образом строим прямую АВ. Точка пересечения прямой линии АВ с линией профиля является искомой точкой К пересечения прямой с топографической поверхностью.
При построении профиля в свободном месте чертежа точки можно построить путём наложения полоски бумаги на план. Отметив их, затем перенести точки на линию условного горизонта. Наиболее часто эти задачи встречаются при проектировании дорог, трубопроводов и других сооружений.
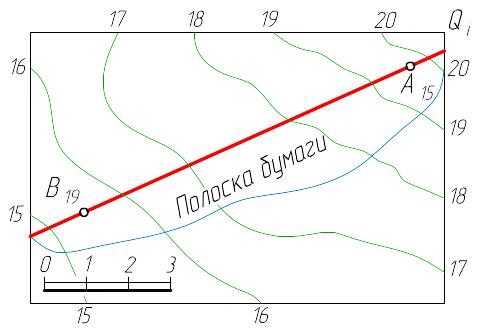
а)
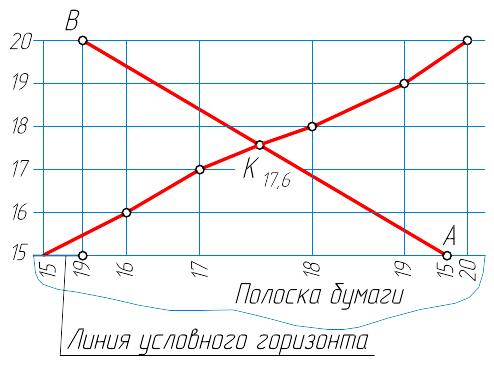
б)
Рисунок 1.9