1.9 Позиционные задачи на поверхностях в проекциях с числовыми отметками

Изображение геометрических тел с помощью горизонталей значительно упрощает построение сечений, так как любая линия сечения может быть выполнена как геометрическое место точек пересечения горизонталей с одинаковыми высотными отметками. На этом принципе выполнялось построение линии пересечения двух плоскостей. Поэтому, решая задачу пересечения гранных или кривых поверхностей плоскостью или прямой, необходимо вначале выполнить градуирование прямолинейных элементов этих поверхностей и построить горизонтали поверхности.

§1.10 Пересечение прямой линии с гранной поверхностью (призмой)

Через заданную прямую MN проводится вспомогательная секущая плоскость, которая определяется прямыми MN и NS и является плоскостью общего положения. Прямая NS параллельна боковым рёбрам призмы. Прямая MS представляет собой линию пересечения секущей плоскости и основания призмы. Боковые грани призмы вспомогательная плоскость пересекает по прямым, параллельным боковым рёбрам. Точки пересечения (С и D) этих прямых с заданной прямой MN будут искомыми (рисунок 1.34).

Рисунок 1.34

§1.11 Пересечение прямой линии с кривыми поверхностями

Через заданную прямую АВ проводится вспомогательная плоскость, которая должна быть общего положения, а не проецирующей. Затем строят пересечение поверхности (прямого кругового конуса) со вспомогательной плоскостью. Необходимо предварительно проградуировать плоскость и поверхность.

Линия пересечения определяется путём построения точек встречи одноименных горизонталей, данной поверхности и вспомогательной плоскости (рисунок 1.35).

Промежуточная точка (N) линии пересечения определяется вспомогательным сечением вертикальной плоскости∑_i, проведённой таким образом, чтобы она рассекала поверхность конуса и плоскость по линии ската. При совмещении сечений точка N' определяется как пересечение гипотенуз прямоугольных треугольников. Опуская перпендикуляр из точки N' на катет, находят промежуточную точку N. На пересечении заданной прямой с полученной линией сечения поверхности находятся искомые точки встречиК_о и К (см.рисунок 1.35).

Рисунок 1.35

§ 1.12 Пересечение гранной поверхности с плоскостью

На рисунке 1.36 показано определение линии пересечения гранной поверхности с плоскостью. Для решения этой задачи градуируют ребра и проводят горизонтали многогранника. Потом две горизонтали каждой грани пересекаются с одноименными горизонталями плоскости, и строятся линии пересечения секущей плоскости с гранями многогранника. Так, на рисунке 1.36 линия пересечения грани ACD плоскостью _i выполнена с помощью горизонталей с высотными отметками 4 и 6, а грань BCD соответственно с горизонталями 5 и 7.

Рисунок 1.36

Другой способ определения линии пересечения с плоскостью (рисунок 1.37): через вершину пирамиды проводим горизонтальную плоскость (вспомогательную плоскость-посредник). Линии основания АВ и ВС, имеющие нулевые отметки, продолжим до горизонтального следа вспомогательной плоскости.

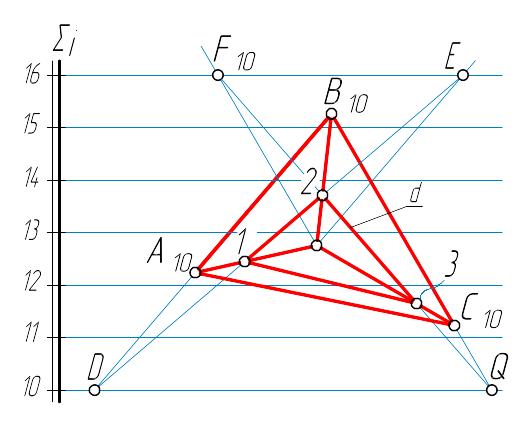
Рисунок 1.37

Соединив точки D иЕ, получаем точки пересечения 1 и 2, соединив точки F и Q - точки пересечения 2 и 3. Соединив точки 1, 2 и З, получим линию пересечения плоскости _i с пирамидой.