1.3 Способы градуированияпрямой в проекциях с числовыми отметками

Концы отрезка прямой часто задаются отметками, которые выражаются дробными числами. Для решения задач в проекциях с числовыми отметками надо знать положение точек с целыми отметками. Установление интервала прямой называется градуированием. Существуют несколько способов градуирования прямой. Все они представляют собой различные варианты решения задач деления в данном отношении. Рассмотрим наиболее распространённые способы решения этой задачи.

Способ совмещения прямой с плоскостью проекции П_о

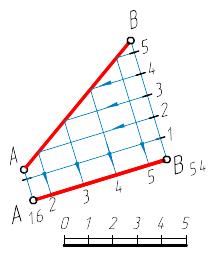
На рисунке 1.6,а показана градуировка отрезка прямой АВ, имеющая дробные отметки: A_l,6 и В_5,4. Для того, чтобы найти на этой прямой между A_l,6 и В_5,4 точки с целыми отметками, из точек A_l,6 и В_5,4 восстановим перпендикуляры к прямой A_l,6В_5,4и откладываем на них отрезки длиной 1,6 и 5,4 м (по линейному или числовому масштабу); соединив концы этих перпендикуляров, получим натуральную величину отрезка прямой АВ и угол наклона прямой к плоскости П_о.

Из точек с отметками 2, 3, 4, 5 на проецирующей прямой (перпендикуляре ВВ_5,4) проводим прямые (рисунок 1.6,б), параллельные прямой A_1,6B_5,4, которые при пересечении с прямой АВ выделят точки с целыми отметками 2', 3', 4', 5', и уже после этого проецируем эти точки на прямую A_l,6 В_5,4.. Когда отметки концов отрезка велики, что усложняет построение, то от точки с большей отметкой откладывают разность отметок градуируемого отрезка (рисунок 1.6,в).

а)	б)	в)

Рисунок 1.6

Способ пропорционального деления отрезка

Теорема (Фалеса): Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

По условию теоремы можно взять любые две прямые. Рассмотрим это на примере. Для этого (рисунок 1.7) из любого конца проекции отрезка проводится прямая под произвольным углом (). На этой прямой в произвольном масштабе откладываются последовательно равные (произвольной длины –с) отрезки. Соединив крайние точки отрезков прямой, проводим через точки деления параллельные ей прямые, которые и определяют положение точек градуирования.

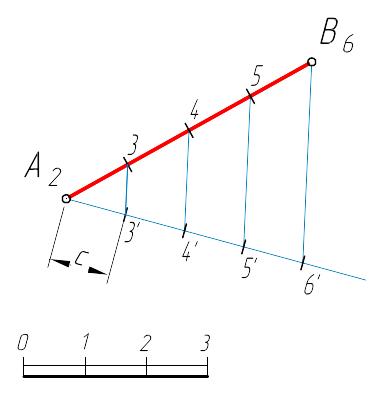
Рисунок 1.7

Аналитический способ градуирования прямой

Величину интервалов и положение точек деления отрезка можно получить вычислением. Зная длину проекции прямой (заложение) L, легко определить величину интервала из отношения

=L/h,

(1.3)

где h – единица превышения.

Рассмотрим на примере (рисунок 1.8) градуирование отрезка прямой аналитическим способом.

Рисунок 1.8

Градуировка с помощью вспомогательного графика

Градуировка с помощью вспомогательного графика выполняется в масштабе чертежа при известном угле наклона  прямой к плоскости (или при заданном уклоне i). При этом величину интервала устанавливают по единичному превышению, согласно которому градуируется отрезок прямой (рисунок 1.9, а и б).

а)	б)

Рисунок 1.9

Градуировка с помощью палетки

Палетка – трафарет, выполненный на прозрачном материале, в виде ряда параллельных линий, расположенных на одинаковом расстоянии.

При градуировании (рисунок 1.10) палетка накладывается на план чертежа, чтобы одна линия палетки прошла через конечную точку проекции отрезка, и путём вращения палетки совмещается второй конец проекции отрезка с (n+1)-й прямой палетки, где n– разность высотных отметок конечных точек градуированной прямой. Для прямой А₄Е₇(n=7-4=3) искомые точки лежат на пересечении проекций отрезка с линиями палетки.

Данный способ градуирования положен в основу пользования «палеткой», применяемой при наводке горизонталей рельефа местности на планах (картах), при измерении площади на планах (что часто используется в инженерной геодезии).

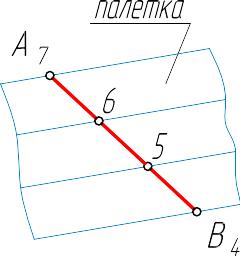
Рисунок 1.10