
- •Ю.И. Самоходов, а.Ю. Абызгильдин, м.М. Абдуллин, п.А. Федоров проекции с числовыми отметками в инженерно-геологической графике
- •Часть I
- •Ю.И. Самоходов, а.Ю. Абызгильдин, м.М. Абдуллин,
- •Введение
- •Проекции с числовыми отметками
- •§1.1 Сущность метода. Точки в проекциях с числовыми отметками
- •§1.2 Параметры прямой в проекциях с числовыми отметками
- •1.3 Способы градуированияпрямой в проекциях с числовыми отметками
- •Аналитический способ градуирования прямой
- •1.4 Взаимное расположение прямых в проекциях с числовыми отметками
- •§ 1.5 Задание плоскости в проекциях с числовыми отметками
- •1.6 Взаимное положение плоскостей в проекциях с числовыми отметками
- •1.7 Прямая и плоскость в проекциях с числовыми отметками
- •1.8 Поверхности в проекциях с числовыми отметками
- •1.9 Позиционные задачи на поверхностях в проекциях с числовыми отметками
- •§1.10 Пересечение прямой линии с гранной поверхностью (призмой)
- •§1.11 Пересечение прямой линии с кривыми поверхностями
- •§ 1.12 Пересечение гранной поверхности с плоскостью
- •§1.13 Пересечение плоскости с прямыми круговыми наклонными конусами
- •Основы компьютерной графики §2.1 Основные команды системы AutoCad
- •§2.2 Подготовительные операции
- •§2.3 Основные операции вычерчивания объектов
- •§ 2.4 Выполнение надписей
- •Нанесение однострочного текста
- •Пример выполнения задания «проекции с числовыми отметками» §3.1 Последовательность выполнения задания по теме «Проекции с числовыми отметками»
- •§3.2 Последовательность выполнения задания в системе AutoCad
- •Библиографический список
- •Приложение а (справочное)
- •Приложение б (справочное) Форматы
- •Приложение в (обязательное) Масштабы
- •Численный масштаб
- •Линейный масштаб
- •Поперечный масштаб
- •Приложение г (обязательное) Линии
- •Приложение д (справочное) Основные надписи
- •Приложение е (рекомендованное) Шрифты чертёжные
- •Профиль топографической поверхности а б в г д е ё ж з и к л м н о п р с т у ф х ц ч ш щ ь ы ъ э ю я
- •Оглавление
- •Часть I
- •450062, Г. Уфа, ул. Космонавтов, 1. Для заметок
Проекции с числовыми отметками
Проекциями с числовыми отметками называют прямоугольные проекции точек на горизонтальную плоскость проекций (можно на любую плоскость) с указанием высоты проекции.
Проекции с числовыми отметками наиболее удобны и рациональны при выполнении чертежей поверхностей сложных криволинейных форм, у которых вертикальные (высотные) размеры незначительны в сравнении с преобладанием горизонтальных размеров.
Проекции с числовыми отметками служат основой для топографических карт и планов. Для выполнения таких чертежей инженерных сооружений, как полотно железных и шоссейных дорог, плотин, дамб, изображений форм залегания пластов в горной и нефтяной промышленности, более рационально применять метод проекций с числовыми отметками
§1.1 Сущность метода. Точки в проекциях с числовыми отметками
Положение в пространстве любой точки, изображаемой в проекциях с числовыми отметками, определяется её прямоугольной проекцией на горизонтальную плоскость По (плоскость нулевого уровня) и указывается в виде индекса в обозначении проекции точки её отметкой. Под отметкой понимают число единиц длины, указывающее расстояние точки до плоскости нулевого уровня. За единицу измерения обычно берут 1 метр. При проецировании земной поверхности за абсолютный нулевой уровень в России принимают постоянный уровень Финского залива (около Кронштадта). При этом все точки, расположенные выше По (принятый за условный нулевой уровень), имеют положительные отметки (рисунок 1.1, точка А) и обозначаются со знаком «+» (плюс), как правило, их не наносят. Точки, расположенные ниже плоскости По, имеют отрицательные отметки (рисунок 1.1, точка В) и обозначаются со знаком «–» (минус). Точки, лежащие в плоскости По, имеют отметки, равные нулю (рисунок 1.1, точка С).
Проекции точек обозначают буквами с соответствующими числами (индексами), их можно обозначать только числовыми отметками, без буквенных обозначений, если это не затрудняет понимание чертежа (рисунок 1.2,б).

Рисунок 1.1
Чертёж, выполненный в проекциях с числовыми отметками, называют планом (картой), обводят рамкой и сопровождают линейным или численным масштабом (приложение Б).
|
|
а) |
б) |
Рисунок 1.2
Прямая в проекциях с числовыми отметками Задание прямой в проекциях с числовыми отметками
Прямую линию в проекциях с числовыми отметками можно задать:
– проекциями двух принадлежащих ей точек с указанием их отметок (рисунок 1.3,а). Разность между отметками концов отрезка определяет положение прямой;
– одной точкой и углом наклона прямой к плоскости По с указанием направления спуска. Прямая в этом случае обозначается одной буквой. Положение прямой может быть задано её уклоном (рисунок 1.3,б);
– одной её точкой, азимутом прямой (Р) и уклоном (i) (рисунок 1.3,в).
|
|
|
а) |
б) |
в) |
Рисунок 1.3
§1.2 Параметры прямой в проекциях с числовыми отметками
Введём некоторые параметры прямой, необходимые для дальнейшего её рассмотрения в проекциях с числовыми отметками (рисунок 1.4) и использования их в решении задач.

Рисунок 1.4
Длина проекции отрезка прямой называется заложением и обозначается буквой L*.
Уклон (i) отрезка прямой равен тангенсу угла наклона прямой к плоскости По:
i=H/L=tg a.
(1.1)
Заложение, приходящееся на единицу превышения (h=l), называется интервалом и обозначается буквой ().Отсюда следует, что уклон и интервал прямой - величины, обратные друг другу, и характеризуют крутизну прямой, и определяются по формуле 1.2
i= l/. |
(1.2) |
Большему интервалу соответствует менее крутая прямая, и наоборот (рисунок 1.5). Интервал т прямой m меньше интервала п прямой n (т<п) при одинаковом превышении (hm=hn).
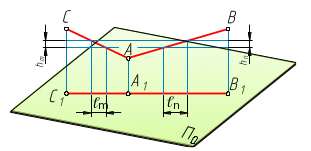
Рисунок 1.5
4 Азимутом () прямой называется угол, отсчитываемый по часовой стрелке от северного направления меридиана до направления уклона прямой.
5 Зенитный угол () –угол отклонения ствола скважины от вертикального положения.





