- •Методические указания по выполнению курсовой работы
- •«Метрологическое обеспечение продукции, процессов и услуг»
- •Аннотация
- •Задание 1 Нахождение показателей точности цилиндрических зубчатых колес и оформление чертежей
- •Задание 2 Статистический анализ точности технологического процесса посредством больших выборок
- •Задание 3 Корреляционно-регрессионный анализ зависимости между двумя переменными
- •Задание 4 Расчет прямолинейного уравнения регрессии и коэффициента корреляции при ограниченном числе опытов
- •Задание 5 Криволинейная корреляционная связь
- •Задание 6 Множественная корреляция
- •Задание 7 Исследование точности измерения линейного размера
Задание 4 Расчет прямолинейного уравнения регрессии и коэффициента корреляции при ограниченном числе опытов
Таблица 1
№ детали |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
7 |
|
|
|
|
|
8 |
|
|
|
|
|
9 |
|
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
Используя данные, полученные в таблице 1, определим значение коэффициента корреляции по следующей зависимости:

Для вывода уравнения регрессии рассчитаем математическое ожидание значений и и СКО соответствующих величин:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Полученные данные подставим в уравнение регрессии:
![]() .
.
Задание 5 Криволинейная корреляционная связь
Если коэффициент корреляции очень мал и прямолинейная связь с отсутствует, то возможна криволинейная связь. Для криволинейных корреляционных связей мерой силы связи является корреляционное отношение, которое определяется зависимостями:
– для связи с
 ,
,
– для связи с
 .
.
Если
с
связаны однозначной связью, то
![]() .
Если связи нет, то
.
Если связи нет, то
![]() .
Аналогичные свойства относятся и к
.
Аналогичные свойства относятся и к
![]() .
Корреляционная связь между
и
будет тем теснее, чем ближе
к 1, и тем слабее, чем
ближе к нулю.
.
Корреляционная связь между
и
будет тем теснее, чем ближе
к 1, и тем слабее, чем
ближе к нулю.
Наиболее
часто наблюдающейся в различных
технических исследованиях криволинейной
корреляционной связью является
параболическая связь, которая выражается
параболой
-го
порядка. Рассмотрим случай, когда
уравнение регрессии
![]() имеет вид второго порядка:
имеет вид второго порядка:
![]() ,
,
где
![]() – постоянные коэффициенты,
– постоянные коэффициенты,
![]() – частное
среднее значение
,
соответствующее различным заданным
значениям
.
– частное
среднее значение
,
соответствующее различным заданным
значениям
.
Для
определения коэффициентов
![]() составляются три уравнения:
составляются три уравнения:
![]() (1)
(1)
где – общее число наблюдений,
![]() – частота
каждого значения
.
– частота
каждого значения
.
Решение этих трех уравнений дает значения коэффициентов .
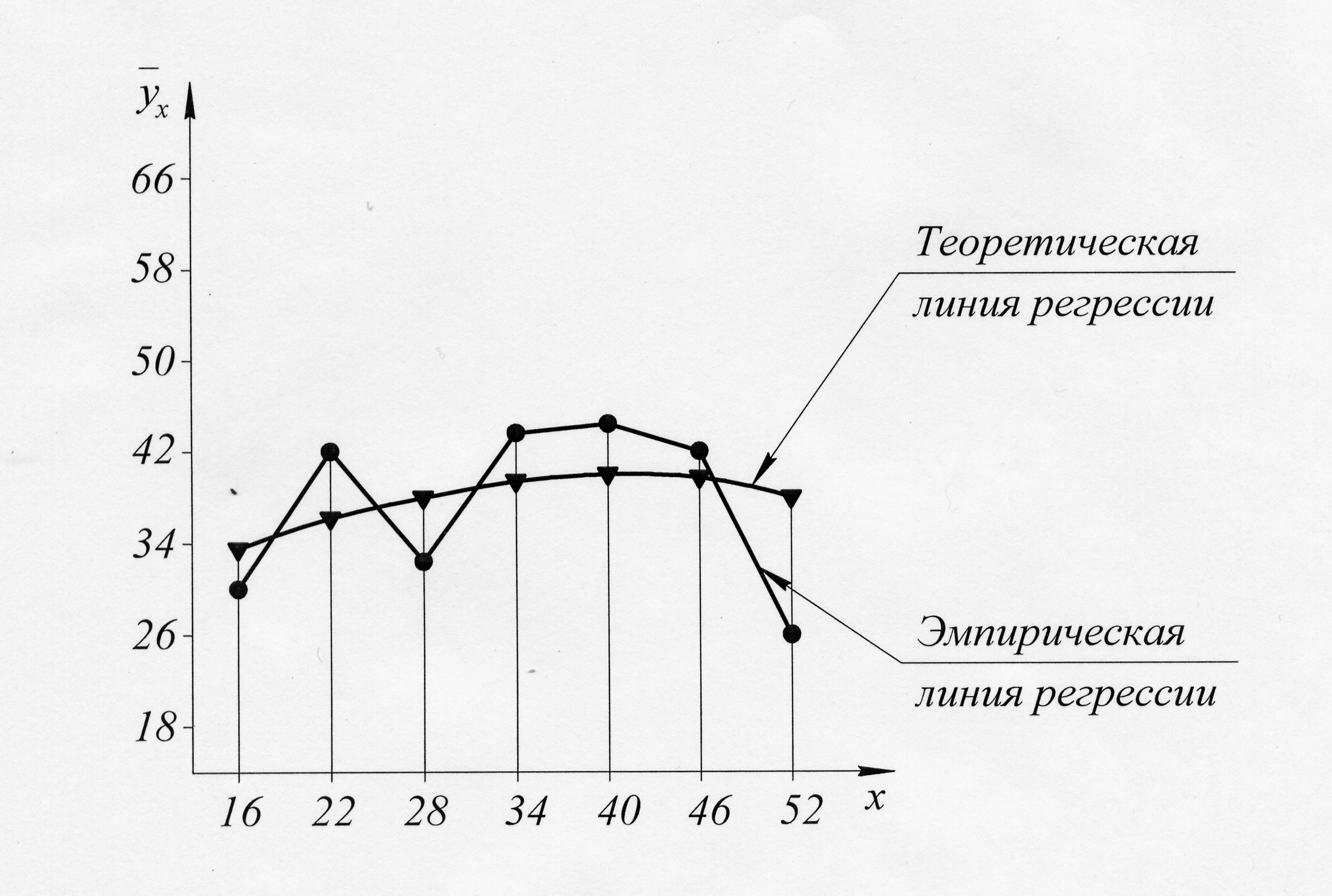
Задание. Вычислить параболическую регрессию для данных, сведенных в корреляционную таблицу.
Таблица 1
Значения |
Значения |
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
- |
|
|
|
Подставим полученные данные в систему уравнений (1).
В
каждом из уравнений разделим числовые
коэффициенты на коэффициент при
![]() .
.
Вычтем из второго уравнения первое, а из третьего уравнения – второе.
Разделим
каждое из этих уравнений на соответствующий
коэффициент при
![]() .
.
![]() Вычтем
из второго уравнения первое.
Вычтем
из второго уравнения первое.
Подставим
![]() в уравнение, получим
.
в уравнение, получим
.
Подставим найденные значения и в уравнение, получим .
Таким образом, уравнение регрессии будет иметь вид
.
Подставив в
полученное уравнение значения
![]() ,
получим теоретические значения частных
средних:
,
получим теоретические значения частных
средних:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|