Лекция 6.4. Работа силового поля. Криволинейный интеграл 2-го рода. Циркуляция и вихрь векторного поля, их вычисления и свойства
6.4.1. Работа силового поля, криволинейный интеграл второго рода
Рассмотрим силовое поле на плоскости
.
Под
действием силы
от точки А
до точки В
по кривой L
движется точка. Требуется вычислить
работу, совершаемую силой
на пути L
(рис. 6.4.1).
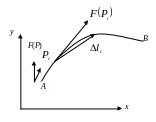
Рис. 6.4.1. Криволинейное движение точки на плоскости xoy под действием переменной силы F
Рис. 6.4.2. Прямолинейное движение точки под действием постоянной силы
Для
прямолинейного
движения и постоянной
силы (
=const)
работа, совершаемая на отрезке
(рис. 6.4.1), равна скалярному произведению
векторов
и l:
где l – направленный отрезок, длина которого равна пройденному пути.
Чтобы
найти работу переменной силы
(x,y)
на криволинейном участке пути L
от А
до В,
очевидно, этот путь нужно разбить на k
маленьких частей так, чтобы каждый
участок пути можно было заменить
направленным отрезком
,
а силу на нем считать постоянной и равной
(Рi)=const
(рис. 6.4.2).
Тогда
работа, совершаемая силовым полем на
i-ом
элементарном участке длиной
приближенно
будет равна скалярному произведению
векторов
Аi ( (Рi)) .
Вся работа на пути L равна сумме элементарных работ
Переходя
к пределу при max
0,
получим точное значение работы,
совершаемой силовым полем на пути L:
Предел, если он существует, называют криволинейным интегралом второго рода, обозначают
,
где
– предельное значение элементарного
направленного отрезка
.
Очевидно, направление
будет совпадать с направлением касательной
к кривой L,
а его модуль равен дифференциалу длины
дуги –
.
Обозначим единичный вектор касательной
–
,
тогда
.
Определение 1. Работа силового поля на криволинейном пути L равна криволинейному интегралу по кривой L от скалярного произведения вектора поля и – элемента касательной к кривой.
,
) (6.4.1)
Выражение
,
)
– называют векторной
формой
криволинейного интеграла второго
рода или
линейным интегралом вектора
.
Скалярное произведение двух векторов {P(x,y), Q(x,y)} и {dx, dy} можно выразить через их координаты:
(6.4.2)
Правая часть равенства (6.4.2) представляет собой координатную форму криволинейного интеграла второго рода. Для пространственной кривой она имеет вид:
(6.4.3)
Следует особо подчеркнуть разницу между физическим смыслом интеграла
– вектора
(второго
рода) и интеграла первого рода
по длине
дуги, который был рассмотрен ранее.
В последнем суммируются значения скалярной функции f(x,y,z), например, плотности массы или заряда, умноженные на – меры элементарных частей кривой L (дифференциалы длины дуги), на которые она дробится. Поэтому, криволинейный интеграл первого рода не зависит от того, в каком направлении проходится кривая L.
Под знаком криволинейного интеграла второго рода
стоит
скалярное произведение двух векторов,
вектора поля
и элемента касательной
,
при этом направление касательной должно
совпадать с выбранным направлением
обхода кривой
L.
Таким образом, в линейном интеграле
вектора
суммируются значения проекций векторной
величины на касательную к кривой в
различных ее точках. Поскольку скалярное
произведение
зависит от угла между векторами
и
знак интеграла
будет зависеть от выбранного обхода
линии L.
Криволинейный интеграл вектора
вычисляют
так же, как криволинейный интеграл
первого рода, т.е. путем сведения к
линейному (определенному) интегралу.
Для этого должно быть задано уравнение
линии L
и направление
ее обхода (либо
координаты начальной и конечной точек).
Если плоская линия L задана в декартовой системе координат уравнением у=у(х), то при сведении интеграла
к линейному, переменную у и dy заменяют их выражением через х из уравнения линии L:
y = y(x),
dy
=
dx.
При параметрическом задании линии L: x=x(t); y=y(t), замену переменных, приводящую к линейному интегралу, осуществляют по формулам:
х=x(t);
dx=
dt;
y=y(t);
dy=
dt.
Пример 1. Вычислить работу силового поля
{cosy, siny}
на отрезке прямой, соединяющей точки А(2; –2), В(–2, 2).
Решение. Работа силового поля равна интегралу
Уравнение линии L, проходящей через точки А(2; –2), В(–2; 2), имеет вид y = – x (рис. 6.4.3).
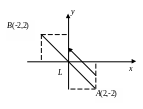
Рис. 6.4.3. Прямолинейный путь в силовом поле (иллюстрация к примеру)
Дифференциал на этой линии dy=–dx. Переменная х меняется от 2 до – 2.
Подставляя в криволинейный интеграл вместо у – уравнение линии, и заменяя dy на – dx получим
,
,
А = – 2sin(2рад) = – 2sin1140 = – 1,827.
В данном случае работа отрицательна. Она совершается в направлении, обратном вектору поля.
Пример 2. Вычислить криволинейный интеграл
,
где
L
– верхняя часть эллипса
,
обход которого проводится по часовой
стрелке (рис. 6.4.4).
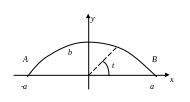
Рис. 6.4.4. Криволинейный путь в плоском силовом поле (иллюстрация к примеру)
Решение. Уравнение эллипса лучше взять в параметрической форме
L: x=acost; y=bsint.
В этом случае вычисления будут значительно проще. Найдем значения параметра в точках начала и конца обхода: в точке А(– а; 0) t1 = , в точке В(а; 0) t2 = 0.
Выразим дифференциалы dx и dy на данной линии через параметр t:
dx=–asintdt; dy=bcostdt.
Заменяя в криволинейном интеграле переменные х и у параметрическим уравнением эллипса и дифференциалы dx и dy, найденными для них значениями на эллипсе, получим:
=
,
,
.
Таким
образом, при обходе верхней части эллипса
под действием силового поля
,
совершается положительная работа.
Пример 3. Вычислить криволинейный интеграл
,
где L – дуга параболы от точки А(0;0) до точки В(2;4).
Решение.
Векторное поле параллельно оси ox:
.
Преобразуем криволинейный интеграл в
линейный, т.е. переменную y
заменим уравнением параболы
и расставим пределы изменения х
при движении от точки А
до точки В:
.
Вычисляя данный интеграл, получим:
.
Работа, совершаемая силовым полем на данном отрезке параболы, отрицательна.
Пример 4. Вычислить криволинейный интеграл
где L – дуга параболы у=х2 от точки А(0;0) до точки В(1;1).
Решение.
Координаты вектора силового поля:
.
Уравнение линии L: у=х2. Дифференциал на этой линии dy=2xdx. Пределы изменения переменной х: 0; 1. Перейдем к линейному интегралу:
.
Вычисляя линейный интеграл, получим:
.
Данное поле на отрезке параболы совершает положительную работу.