6.3.4. Дивергенция векторного поля
Важной характеристикой векторного поля является его дивергенция (или расхождение), которая определяется в каждой точке области, где задано поле.
Пусть дано векторное поле в некоторой области D:
.
Возьмем
произвольную точку
и окружим ее замкнутой поверхностью
(рис. 6.3.7).
В качестве положительной нормали к
поверхности будем считать внешнюю
нормаль.
Поток в направлении внешней нормали называют потоком изнутри поверхности.
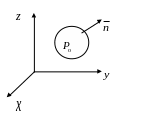
Рис. 6.3.7. Замкнутая поверхность в произвольном векторном поле
Рис. 6.3.8. Замкнутая поверхность в потоке жидкости
Пример 4. Представим мысленно, что замкнутая поверхность расположена в равномерном потоке текущей жидкости и жидкость свободно проникает через ее стенки (рис. 6.3.8).
Поток изнутри поверхности будет равен нулю, так как сколько втекает жидкости в данную поверхность, столько и вытекает.
Вернемся
к произвольному векторному полю,
заданному в области
.
Найдем количество векторных линий этого
поля, которые возникают в единицу времени
в единице объема
,
заключенного внутри поверхности
.
Очевидно, что оно равно величине потока
изнутри поверхности, деленной на объем,
т.е.
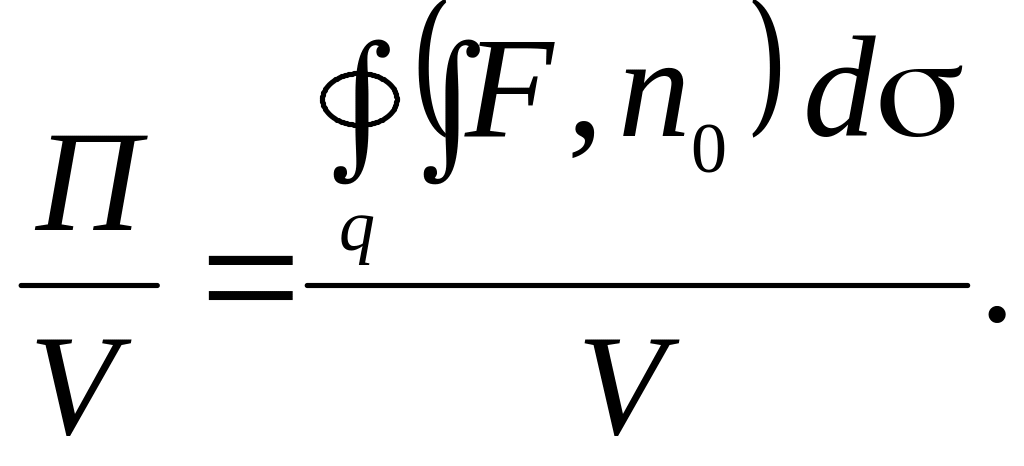
Данное отношение, определяющее количество возникающих векторных линий в единице объема, характеризует среднюю объемную мощность источника, или мощность стока (для отрицательных потоков изнутри поверхности ).
Чтобы
найти, сколько образуется векторных
линий в единицу времени в точке
,
нужно перейти к пределу при
,
т.е. при стягивании объема в точку
.
Предел, если он существует, называют дивергенцией, или расхождением векторного поля в точке и обозначают
div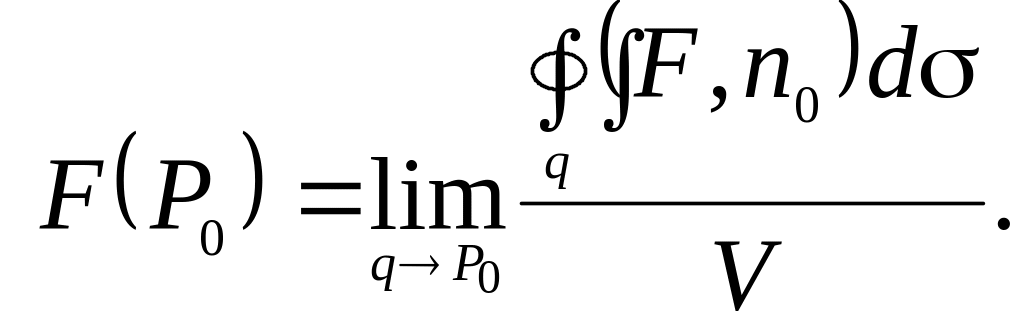
Определение 4. Дивергенция (или расходимость) – это скалярная величина, характеризующая мощность источников или стоков векторного поля в каждой его точке. Она равна пределу потока векторного поля через замкнутую поверхность, отнесенного к объему, заключенному внутри поверхности, при стягивании поверхности в точку.
Если векторное поле в области задано тремя скалярными функциями – проекциями вектора поля на координатные оси
,
то дивергенцию поля в произвольной точке находят по формуле
div
(6.3.5)
при
этом предполагается, что функции
,
,
во всех точках области имеют непрерывные
частные производные.
Замечание 1. В формуле (6.3.5) не пишут индекс , так как эта формула справедлива в любой точке поля.
Замечание 2. Для плоского поля в правой части формулы (6.3.5) отсутствует третье слагаемое.
Отметим некоторые свойства дивергенции.
1.
Если
– постоянный вектор, то div
2.
div
div
+
div
,
где
и
– произвольные постоянные.
3.
Если
– скалярная функция,
– вектор, то
div
div
+
gradU.
Доказательство:
div
gradU+U
div
.
Пример
5. Найти
дивергенцию однородного поля
const.
Решение. Проекции вектора поля на координатные оси
const,
const,
const
имеют вид
div
Однородное поле не имеет источников.
Пример 6. Найти дивергенцию радиус-вектора.
Решение.
Координаты радиус-вектора
.
div
Каждая точка поля радиус-вектора является источником мощности 3.
Пример
7. Доказать
равенство div
grad
f
div
.
Решение.
Пусть
.
Тогда
и
div
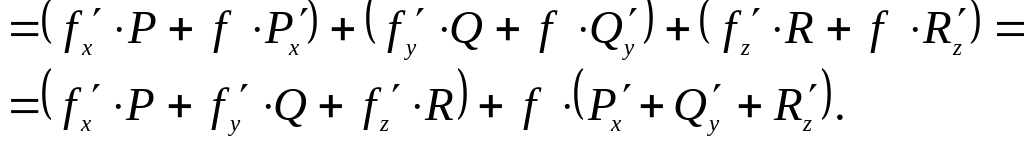
В первой скобке стоит скалярное произведение градиента скалярного поля f на вектор F, а во второй – дивергенция векторного поля F. Таким образом, div grad f div .
Дивергенция – это локальная характеристика векторного поля. Она характеризует свойства поля в точках и бесконечно малых окрестностях, прилегающих к этим точкам.