Лекция 6.3. Поток векторного поля и его вычисление. Дивергенция векторного поля, вычисление, свойства. Теорема остроградского-гаусса

6.3.1. Поток векторного поля

Во многих физических и технических задачах приходится находить потоки векторных полей через различные поверхности, например, поток жидкости через определенное поперечное сечение, поток воздуха и т. д. Это привело к необходимости различать двусторонние и односторонние поверхности.

6.3.1.1. Односторонние и двусторонние поверхности

Определение 1. Поверхность называют двусторонней, если нормаль к поверхности при обходе по любому замкнутому контуру, лежащему на этой поверхности и не имеющему общих точек с ее границей, возвращается в первоначальное положение.

Проще говоря, поверхность называют двусторонней, если у нее можно различить две стороны. У таких поверхностей с одной стороны на другую можно перейти только через край (рис. 6.3.1).

Однако существуют поверхности, у которых нельзя различить две стороны. Они получили название односторонних. Примером односторонней поверхности является лист Мебиуса. Модель его легко сделать из полоски бумаги, если склеить края этой полоски предварительно перекрутив ее.

Выйдя из какой-нибудь точки лиса Мебиуса с определенным направлением нормали, можно, двигаясь непрерывно и нигде не пересекая границы листа, прийти в ту же точку с противоположным направлением нормали. Это значит, что при закрашивании одной поверхности листа Мебиуса мы закрасим его целиком, не оставив места для другого цвета.

В дальнейшем мы будем рассматривать только двусторонние поверхности.

Определение 2. Гладкая поверхность в трехмерном пространстве называется двусторонней, если нормаль к поверхности при обходе по любому замкнутому контуру, лежащему на поверхности и не имеющему общих точек с ее границей, возвращается в первоначальное положение.

Двусторонняя поверхность считается ориентированной, если на ней задано (в зависимости от условий физической задачи) положительное направление единичного вектора нормали или выбрана положительная сторона поверхности.

Рис.6.3.1. Двусторонняя поверхность, – нормаль к поверхности

Итак, пусть векторное поле образовано вектором. Для наглядности будем считать вектором скорости некоторого потока жидкости, движущейся стационарно. Представим, что некоторая поверхность находится в этом потоке и пропускает жидкость. Подсчитаем, какое количество жидкости протекает через поверхность .

Выберем определенную сторону поверхности . Пусть

–

единичный вектор нормали к рассматриваемой стороне поверхности . Разобьем поверхность на элементарные площадки . Выберем в каждой площадке точку и вычислим значения вектора скорости в каждой точке .

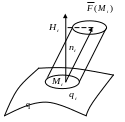
Рис. 6.3.2. Иллюстрация к вычислению потока векторного поля

Будем приближенно считать каждую площадку плоской, а вектор постоянным по модулю и одинаково направленным в каждой точке площадки. Тогда за единицу времени через протекает количество жидкости, приближенно равное П , где – площадь -й площадки, – высота -го цилиндра с образующей . Но является проекцией вектора на нормаль : Пр , где – единичный вектор нормали к поверхности в точке . Следовательно, общее количество жидкости, протекающее через всю поверхность за единицу времени, найдем, вычислив сумму

П

Точное значение искомого количества жидкости получим, взяв предел найденной суммы при неограниченном увеличении числа элементарных площадок и стремлении к нулю их размеров (диаметров площадок):

П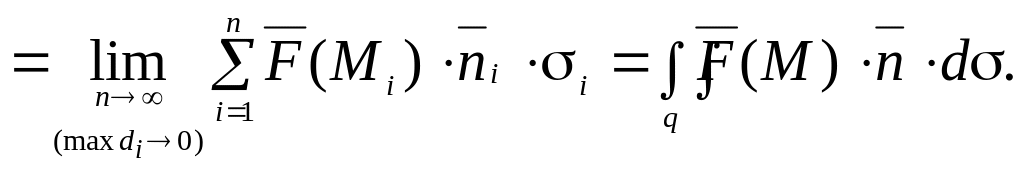

Независимо от физического смысла поля полученный интеграл называют потоком векторного поля.

Определение 3. Поверхностный интеграл второго рода от скалярного произведения вектора поля на единичный вектор нормали к поверхности

П (6.3.1)

называется потоком векторного поля через поверхность .

Рассмотрим различные формы записи потока вектора. Так как

Пр Пр ,

то

П ,

где – проекция вектора на направление нормали , – дифференциал площади поверхности.

Иногда формулу (6.3.1) записывают в виде

П ,

где вектор направлен по нормали к поверхности, причем (т.е. элементарную часть поверхности , снабженную единичной нормалью , обозначают вектором, длина которого равна ее площади ).

Так как

, ,

где , , – проекции вектора на соответствующие координатные оси, то поток (6.3.1) вектора , можно записать в виде

П

Используя взаимосвязь поверхностных интегралов 1-го и 2-го рода, поток вектора можно записать как

П (6.3.2)

Заметим, что под знаком поверхностного интеграла второго рода стоит скалярное произведение двух векторов, величина которого зависит от угла между вектором поля и нормалью к поверхности. Следовательно, для выбранного направления нормали поверхностный интеграл второго рода зависит от того, по какой стороне поверхности он вычисляется.

Если угол между нормалью и вектором поля в каждой точке поверхности острый, то поток векторного поля через такую поверхность положителен, если этот угол во всех точках поверхности тупой, то поток отрицателен.

Отметим, что поток вектора есть скалярная величина. Величина П равна объему жидкости, которая протекает через поверхность за единицу времени. В этом состоит физический смысл потока (независимо от физического смысла поля).

Особый интерес представляет случай, когда поверхность замкнута и ограничивает некоторый объем . Тогда поток вектора записывается в виде

П .

В этом случае за направление вектора обычно берут направление внешней нормали и говорят о потоке изнутри поверхности q.

Если векторное поле есть поле скоростей текущей жидкости, то величина потока П через замкнутую поверхность дает разность между количеством жидкости, вытекающей из области и втекающей в нее за единицу времени.

Из физических соображений ясно, что если П , то из области вытекает больше жидкости, чем втекает. Это означает, что внутри области имеются дополнительные источники.

Если П , то внутри области имеются стоки, поглощающие избыток жидкости.

Можно сказать, что источники – точки, откуда векторные линии начинаются, а стоки – точки, где векторные линии заканчиваются. Так, в электростатическом поле источником является положительный заряд, стоком – отрицательный заряд магнита.

Если П , то из области вытекает столько же жидкости, сколько в нее втекает в единицу времени; внутри области либо нет ни источников, ни стоков, либо они таковы, что их действие взаимно компенсируется.