
- •Раздел 6. Элементы теории поля 557
- •Раздел 6. Элементы теории поля лекция 6.1. Скалярное поле. Понятие линий и поверхностей уровня. Производная по направлению. Градиент
- •6.1.1 Основные понятия
- •6.1.2 Скалярное поле
- •6.1.3. Характеристики скалярного поля
- •6.1.3.1. Поверхности и линии уровня
- •6.1.3.2. Производная по направлению
- •6.1.3.3. Градиент скалярного поля и его свойства
- •Свойства градиента
- •Лекция 6.2. Векторное поле. Векторные линии векторного поля
- •6.2.1. Векторное поле
- •6.2.2. Векторные линии
- •Лекция 6.3. Поток векторного поля и его вычисление. Дивергенция векторного поля, вычисление, свойства. Теорема остроградского-гаусса
- •6.3.1. Поток векторного поля
- •6.3.1.1. Односторонние и двусторонние поверхности
- •6.3.2. Вычисление потока векторного поля путем сведения к трем двойным интегралам
- •6.3.3. Вычисление потока векторного поля путем сведения к одному двойному интегралу
- •6.3.4. Дивергенция векторного поля
- •6.3.5. Теорема Остроградского-Гаусса
- •Лекция 6.4. Работа силового поля. Криволинейный интеграл 2-го рода. Циркуляция и вихрь векторного поля, их вычисления и свойства
- •6.4.1. Работа силового поля, криволинейный интеграл второго рода
- •6.4.2. Циркуляция и ротор векторного поля
- •Лекция 6.5. Формулы стокса и грина
- •6.5.1. Формулы Грина и Стокса
- •Лекция 6.6. Векторные дифференциальные операции первого и второго порядка. Специальные виды векторных полей и их свойства
- •6.6.1. Векторные дифференциальные операции первого порядка
- •6.6.2. Векторные дифференциальные операции второго порядка
- •6.6.3. Простейшие векторные поля
- •6.6.3.1. Потенциальное поле
- •6.6.3.2. Соленоидальное поле
- •6.6.3.3. Гармоническое поле
- •Контрольные вопросы и заданая для самопроверки
- •15. Гармоническое поле
Свойства градиента
1.
Проекция градиента поля
в точке
![]() на какое-либо направление
равна скорости изменения
в данном направлении.
на какое-либо направление
равна скорости изменения
в данном направлении.
2. Если в точке градиент отличен от нуля, то он перпендикулярен линии или поверхности уровня, проходящей через эту точку, и направлен в сторону возрастания значений поля , так как направление градиента – это направление наибыстрейшего возрастания значений функции .
3.
Если
и
![]() – скалярные поля, определенные в одной
и той же области
,
то в любой точке этой области справедливы
соотношения, вытекающие из правил
нахождения производных:
– скалярные поля, определенные в одной
и той же области
,
то в любой точке этой области справедливы
соотношения, вытекающие из правил
нахождения производных:
а)
grad![]() grad
+grad
grad
+grad![]() ,
,
б)
grad![]() grad
,
c=const,
grad
,
c=const,
в)
grad![]() vgrad
+
grad
,
vgrad
+
grad
,
д)
grad![]() ,
,
е)
grad![]() grad
.
grad
.
Пример
4. Найти
градиент скалярного поля
![]() в точке
в точке
![]() .
.
Решение. Проекции градиента на координатные оси равны значениям частных производных поля в точке :
![]() ;
;
![]() ;
;
![]() .
.
Следовательно,
grad![]() .
.
Пример
5. Найти
направление градиента и наибольшую
скорость возрастания функции
![]() в точке
в точке
![]() .
.
Решение. Найдем сначала проекции градиента на координатные оси в точке . Имеем:
grad![]() ,
,
grad![]() .
.
Наибольшая скорость возрастания скалярного поля равна модулю градиента в точке :
|grad
|![]() .
.
Направление вектора градиента определяется его направляющими косинусами:
![]() ,
,
![]() ,
,
![]() .
.
Вывод: мы ввели понятие поля и скалярного поля, рассмотрели примеры скалярных полей и его характеристики – поверхности уровня (геометрическая характеристика), производная по направлению (числовая характеристика) и вектор градиент.
Лекция 6.2. Векторное поле. Векторные линии векторного поля
6.2.1. Векторное поле
Рассмотрим частные случаи векторных полей.
Однородное
векторное поле.
Если в каждой точке области, где задано
поле, вектор
имеет одинаковое направление и одну и
ту же длину, т.е.
![]() –
постоянные величины, то векторное поле
называют однородным. Примером однородного
поля является поле сил тяжести в случаях
небольшой высоты над землей (рис. 6.2.1).
–
постоянные величины, то векторное поле
называют однородным. Примером однородного
поля является поле сил тяжести в случаях
небольшой высоты над землей (рис. 6.2.1).
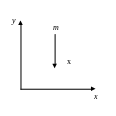
Рис. 6.2.1. Схематическое изображение поля сил тяжести
Плоско-параллельное
поле.
В тех случаях, когда в выбранной системе
координат проекции вектора не зависят
от одной из переменных, например,
![]()
![]()
![]() то поле называют плоско-параллельным.
Такое поле изображено на рис. 6.2.2.
то поле называют плоско-параллельным.
Такое поле изображено на рис. 6.2.2.
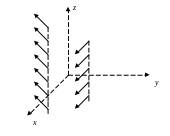
Рис.6.2.2. Плоско-параллельное поле
Вдоль
прямых, параллельных оси
,
величина и направление вектора
не изменяются. При изучении такого поля
можно рассматривать его разрез плоскостью,
параллельной плоскости
![]() .
Во всех других параллельных плоскостях
картина будет та же самая. Если при этом
проекция вектора
на ось
во всех точках плоскости
будет равна нулю, то поле называют
плоским. Плоские поля очень часто
встречаются при изучении поля скоростей
в потоке жидкости.
.
Во всех других параллельных плоскостях
картина будет та же самая. Если при этом
проекция вектора
на ось
во всех точках плоскости
будет равна нулю, то поле называют
плоским. Плоские поля очень часто
встречаются при изучении поля скоростей
в потоке жидкости.
6.2.2. Векторные линии
Рассмотрим
векторное поле, задаваемое вектором
![]() .
Изучение поля удобно начинать с понятия
векторных линий, они являются простейшими
геометрическими характеристиками поля.
.
Изучение поля удобно начинать с понятия
векторных линий, они являются простейшими
геометрическими характеристиками поля.
Определение 1. Векторной линией поля называется линия, в каждой точке которой вектор поля направлен по касательной к этой кривой.
Это понятие для конкретных полей имеет ясный физический смысл. Например, в поле скоростей текущей жидкости векторными линиями будут линии, по которым движутся частицы жидкости, для магнитного поля векторными линиями будут линии, выходящие из северного полюса и оканчивающиеся в южном.
В поле точечного электрического заряда векторные линии совпадают с силовыми линиями и являются лучами, выходящими из заряда (рис. 6.2.3).
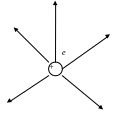
Рис.6.2.3.
Векторные линии электростатического
поля
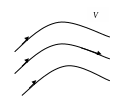
Рис.6.2.4. Векторные линии в поле скоростей текущей жидкости
Если мы имеем поле скоростей текущей жидкости (рис. 6.2.4), то векторные линии такого поля являются траекториями движения частиц или линиями тока жидкости.
Определение 2. Векторной трубкой называют поверхность, образованную векторными линиями, проходящими через точки некоторой замкнутой кривой, расположенной в данном поле и не совпадающей ни с одной из векторных линий.
В любой точке поверхности векторной трубки вектор поля направлен по касательной к поверхности (рис. 6.2.5).

Рис. 6.2.5. Векторная трубка
Рис.6.2.6. Схематическое изображение векторной линии
Выведем дифференциальное уравнение для семейства векторных линий в декартовой системе координат. Пусть силовое поле задано тремя скалярными функциями
.
Одна из векторных линий этого поля изображена на рис. 6.2.6. Вектор касательной к этой линии имеет координаты
![]() .
.
По
определению, вектор поля
в каждой точке векторной линии совпадает
с направлением касательной, т.е.
![]() .
.
Условие коллинеарности двух векторов дает систему дифференциальных уравнений первого порядка:
![]() .
.
Решая эту систему, можно найти уравнение линий в пространстве или как пересечение двух поверхностей, или в параметрической форме.
Пример
1. Найти
векторные линии поля
![]() .
.
Решение. Система дифференциальных уравнений векторных линий имеет вид:
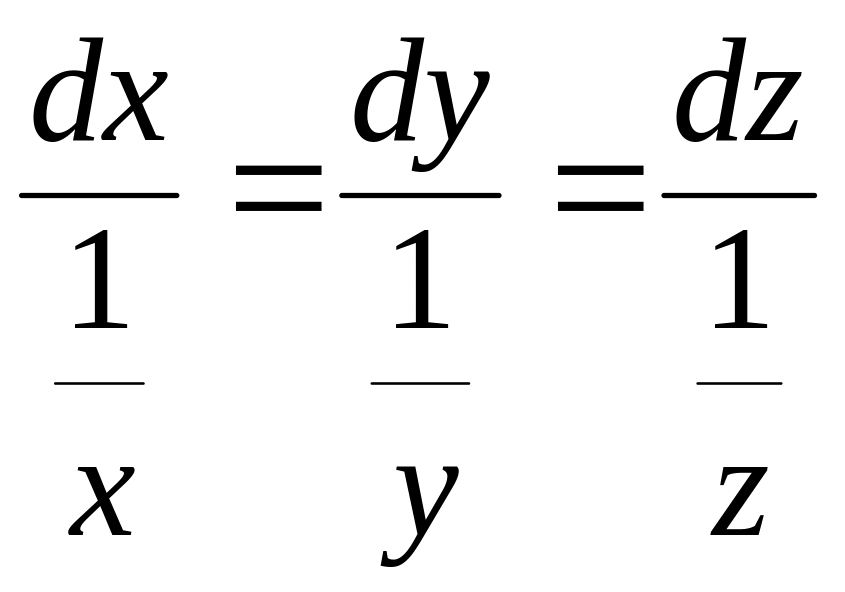
или
![]() ,
,
интегрируя левую и правую части последних равенств, получим общее решение системы в виде
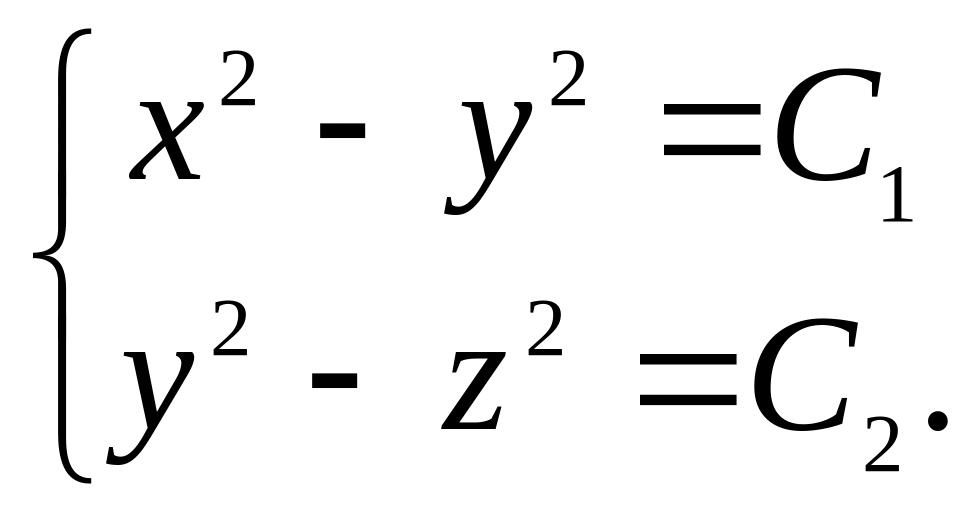
Уравнение
![]() представляет собой семейство
гиперболических цилиндров с образующими,
параллельными оси
.
Второе уравнение дает семейство
цилиндрических поверхностей, с
образующими, параллельными оси
.
Таким образом, векторные линии задаются
пересечением гиперболических цилиндров.
представляет собой семейство
гиперболических цилиндров с образующими,
параллельными оси
.
Второе уравнение дает семейство
цилиндрических поверхностей, с
образующими, параллельными оси
.
Таким образом, векторные линии задаются
пересечением гиперболических цилиндров.
Пример
2. Дано
однородное векторное поле, т.е.
![]() const,
или
const,
или
![]() ,
,
![]() ,
,
![]() ,
,
,
![]() и
и
![]() – постоянные. Найти уравнение векторных
линий.
– постоянные. Найти уравнение векторных
линий.
Решение. Запишем систему дифференциальных уравнений в виде
![]()
где
![]() – параметр. Откуда следует
– параметр. Откуда следует
![]() ;
;
![]() ;
;
![]() .
.
Интегрируя обе части последних равенств, получим общее решение системы:
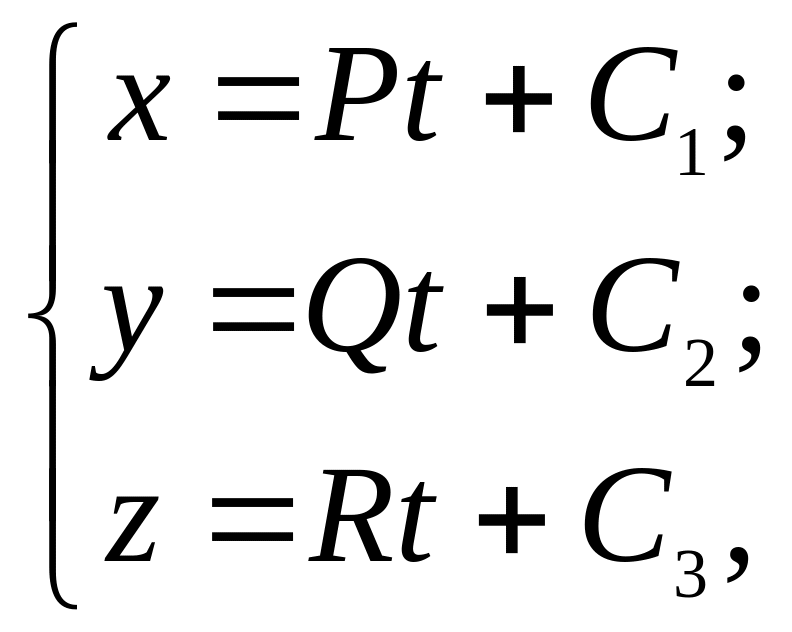
где
![]() ,
,
![]() ,
,
![]() – произвольные постоянные.
– произвольные постоянные.
Нетрудно
заметить, что общее решение является
параметрическим уравнением семейства
прямых в
пространстве, проходящих через точки
с координатами (
,
,
),
и имеющих одинаковый направляющий
вектор
![]() .
Таким образом, векторные линии однородного
векторного поля – это семейство прямых,
параллельных
вектору поля
.
Таким образом, векторные линии однородного
векторного поля – это семейство прямых,
параллельных
вектору поля
![]() .
.
Пример
3. Найти
векторные линии поля
![]() .
.
Решение. Составим систему дифференциальных уравнений для данного векторного поля
![]() .
.
Интегрирование
уравнения
![]() дает семейство круговых цилиндров,
параллельных оси
,
с радиусами
дает семейство круговых цилиндров,
параллельных оси
,
с радиусами
![]() :
:
![]() ,
где
,
где
![]() .
.
Чтобы решить второе дифференциальное уравнение
![]() ,
,
введем параметр . Семейство найденных цилиндров в параметрической форме:
![]() ,
,
![]() .
.
Подставим
и
![]() ,
выраженные через параметр
,
во второе дифференциальное уравнение
,
выраженные через параметр
,
во второе дифференциальное уравнение
![]() ,
или
,
или
![]() .
.
Интегрируя последнее равенство, получим
![]() .
.
Векторные линии задаются параметрически следующей системой уравнений:
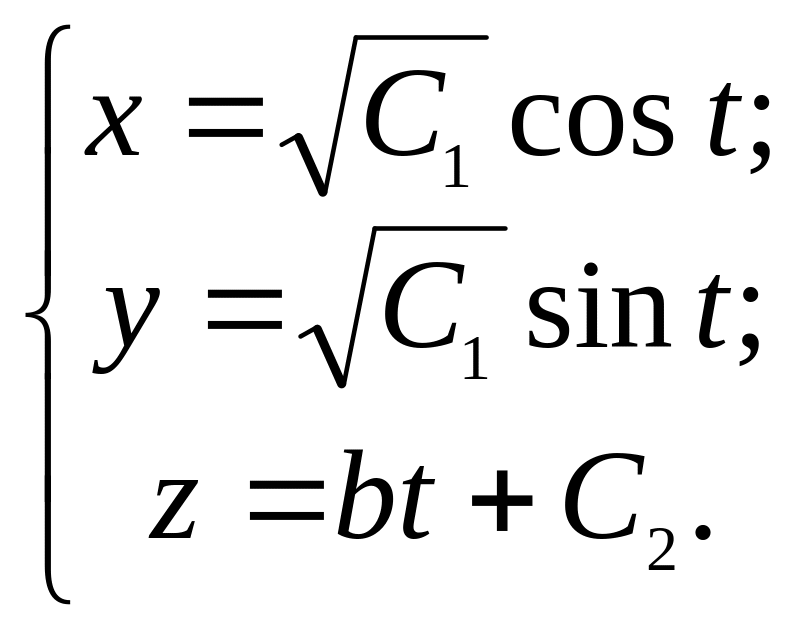
Они представляют собой семейство винтовых линий.
Вывод: мы ввели определение векторного поля, привели примеры векторных полей и ввели геометрическую характеристику векторного поля – векторные линии.
