6.1.3.2. Производная по направлению

Числовой характеристикой скалярного поля является производная по направлению.

Известно, что скорость изменения значений функции в точке в направлении координатных осей равна частным производным по соответствующим переменным. Следовательно, чтобы найти скорость изменения поля в точке в направлении , нужно взять производную от функции в этой точке по данному направлению.

Определение 5. Производная скалярного поля по направлению , заданному вектором , вычисляется по формуле

, (6.1.1)

где , , – направляющие косинусы вектора , – модуль вектора .

В случае плоского поля имеем:

, ,

и формула (6.1.1) принимает вид

.

Замечание. Понятие производной по направлению является обобщением понятия частных производных , , . Их можно рассматривать как производные от функции по направлению координатных осей , и . Так, если направление совпадает с положительным направлением оси , то, положив в формуле (6.1.1) , , , получим .

Производная по направлению характеризует скорость изменения функции в точке в заданном направлении. Если , то функция возрастает в направлении , если то функция в направлении убывает. Кроме того, величина представляет собой мгновенную скорость изменения функции в направлении : чем больше , тем быстрее изменяется функция .

Пример 3. Найти скорость изменения скалярного поля, заданного функцией

,

в точке в направлении вектора , если .

Решение. Найдем координаты вектора :

, направляющие косинусы данного вектора будут равны:

, , .

Вычислим значение частных производных в точке :

,

,

.

Скорость изменения значений функции в точке найдем по формуле

.

Таким образом, значения скалярной величины в точке в направлении убывают со скоростью .

Итак, чтобы найти скорость изменения скалярного поля в некоторой точке в данном направлении, нужно вычислить частные производные в этой точке и умножить их на соответствующие направляющие косинусы вектора, в направлении которого находится скорость.

6.1.3.3. Градиент скалярного поля и его свойства

Векторной характеристикой скалярного поля является вектор градиент.

Рассмотрим скорость изменения поля в точке в произвольном направлении . Она задается формулой

,

где , , – направляющие косинусы вектора или проекции на координатные оси его единичного вектора:

, .

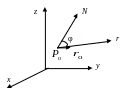
Рис. 6.1.3. Иллюстрация к понятию вектора градиента

Из векторной алгебры известно, что если даны два вектора своими разложениями по ортам , , , т.е.

, ,

то их скалярное произведение

.

Сравнивая эту формулу со скоростью изменения поля в точке в направлении , легко заметить, что является скалярным произведением двух векторов:

, .

Пусть угол между этими векторами равен , тогда можно записать так:

.

Таким образом, скорость изменения поля в точке в произвольном направлении равна проекции некоторого вектора на это направление. Вектор называют градиентом скалярного поля в точке .

Определение 6. Градиентом скалярного поля в точке называют вектор, длина которого равна максимальной скорости изменения поля в этой точке. Обозначается

grad (6.1.2)

Поставим вопрос: по какому направлению производная самая большая? Согласно формуле

Пр (grad grad ,

этот вопрос сводится к следующему: на какое направление проекция вектора grad самая большая? Очевидно, что любой вектор при проектировании на различные направления дает самую большую проекцию, равную его модулю, при проектировании на его собственное направление. Таким образом, вектор grad в точке указывает в сторону самого быстрого возрастания поля , причем эта наибольшая скорость в расчете на единицу длины равна |grad |. На рис. 6.1.4 показаны векторы градиента температуры в отдельных точках теплопроводящей среды, подогреваемой изнутри, из затемненной зоны, и охлаждаемой снаружи. Градиент температуры направлен к «печке».

Полученный физический смысл градиента показывает также, что градиент инвариантно связан с рассматриваемым полем, т.е. остается неизменным (инвариантным) при замене декартовых осей. (Этого не было видно из определения градиента (6.1.2), данного в «неинвариантной» форме, «привязанной» к какой-то одной системе координат.) Более того, если задано поле , то в каждой точке пространства можно найти направление и скорость наибыстрейшего возрастания поля ; так, можно найти вектор grad , не прибегая к координатам. Итак, градиент скалярного поля образует вполне определенное векторное поле.

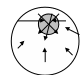
Рис. 6.1.4. Пример вектора градиента температуры в теплопроводящей среде