
Яблонский Вариант 11 / С-6 вар 11 / C6(11)
.PDF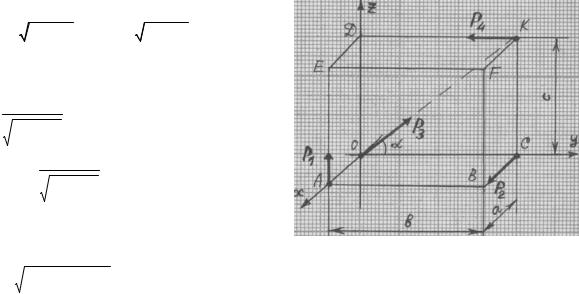
C6(11)
Определить главный вектор |
RG * |
и главный момент |
|
M O |
системы сил относительно центра |
||||||||||||||||
О и установить, к какому простейшему виду приводится эта система. |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Размеры |
|
|
|
|
|
Силы системы |
|
|
|
|
|
||||||||
|
прямоугольного |
|
|
|
|
|
|
|
|
|
|||||||||||
|
параллелепипеда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
P1 |
|
|
P2 |
|
|
|
|
P3 |
|
|
P4 |
|
|
||||||
|
|
|
см |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a |
|
b |
|
c |
модуль, Н |
точка приложения |
направление |
модуль, Н |
точка приложения |
|
направление |
|
модуль, Н |
|
точка приложения |
направление |
модуль, Н |
точка приложения |
направление |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
40 |
|
30 |
8 |
A |
AE |
12 |
C |
|
CB |
|
20 |
|
O |
OK |
16 |
K |
KD |
|
Решение
1. Определение модуля и направления главного вектора заданной системы сил по его проекциям на координатные оси.
Проекции главного вектора на оси координат (рис. 1):
cosα = |
b |
|
|
, sin α = |
|
c |
|
||||||||
b2 +c2 |
|
b2 +c2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
X = P2 = 12 |
|
|
H |
|
|
|
|
|
|
||||||
Y = |
|
b |
|
|
P3 − P4 = 0 |
||||||||||
|
|
b2 + c2 |
|
|
|
|
|
|
|
|
|
||||
Z = |
P1 + |
|
|
c |
|
|
|
P3 = 20 |
H |
||||||
|
|
|
|
b2 + c2 |
|
|
|
|
|
|
|||||
Модуль главного вектора |
|
|
|
||||||||||||
R* = |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1. |
|
|
X2 + Y2 + Z2 = 23.32 H |
||||||||||||||
Направляющие косинусы |
|
|
|
||||||||||||
|
G |
* |
G |
|
|
X |
|
|
|
12 |
|
= 0.515 |
|||
cos(R |
|
, i ) |
= |
|
|
= |
|
|
|
||||||
|
|
R* |
23.32 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
G |
* |
G |
|
|
Y |
|
|
|
|
0 |
|
= 0 |
|
|
cos(R |
|
, j ) |
= |
|
|
|
= |
23.32 |
|
|
|||||
|
|
R* |
|
||||||||||||
|
G |
* |
G |
|
|
Z |
|
|
|
20 |
|
|
|
|
|
cos(R |
|
, k ) |
= |
|
|
|
= |
|
|
|
= 0.858 |
||||
|
|
R* |
|
23.32 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||

2.Определение главного момента заданной системы сил относительно центра О.
Главные моменты заданной системы сил относительно координатных осей:
MX = |
c P4 = 480 |
|
Н·см |
|
|
|
|
|||||
МY = −a P1 = −80 Н·см |
|
|||||||||||
MZ = |
−b P2 = −480 |
|
|
Н·см |
|
|||||||
M = |
M 2 |
+ M 2 + M 2 |
= 683.5 |
Н·см |
||||||||
O |
x |
y |
|
|
|
|
z |
|
|
|
|
|
Направляющие косинусы: |
|
|
|
|
|
|
|
|||||
|
G |
G |
M |
|
|
|
|
480 |
|
= 0.702 |
||
|
cos(MO |
, i ) = |
|
|
X |
= |
|
|
|
|||
|
|
|
683.5 |
|
||||||||
|
|
MO |
|
|||||||||
|
G |
G |
|
|
|
|
|
|||||
|
M |
|
|
|
|
|
−80 |
= −0.117 |
||||
|
cos(MO |
, j ) = |
|
Y |
|
= |
|
|
|
|||
|
MO |
|
683.5 |
|
||||||||
|
G |
G |
|
|
|
|
|
|||||
|
M |
Z |
|
|
|
|
−480 |
|
||||
|
cos(MO |
, k ) = |
|
|
= |
|
|
|
= −0.702 |
|||
|
MO |
|
|
683.5 |
|
|||||||
|
|
|
|
|
|
|
|
|
||||
3. Вычисление наименьшего главного момента заданной системы сил.
M * = |
X M X +Y M Y + Z M Z |
= −164.6 |
Н·см |
|
|||
|
R* |
|
|
4. Так как R* ≠ 0, M * ≠ 0 , то заданная система сил приводится к динаме (силовому винту) рис. 2.
Уравнение центральной оси:
M X −( y Z −z Y ) |
= |
M Y −(z X −x Z ) |
= |
M Z −(x Y − y X ) |
= |
M * |
. |
|
X |
Y |
Z |
R* |
|||||
|
|
|
|
Подставляя в это уравнение найденные числовые значения величин, находим:
(1)564.7 − 20 y = 0
(2)−80 − 12 z + 20 x = 0
Координаты точек пересечения центральной осью координатных плоскостей определяем при помощи уравнений центральной оси (1) и (2) . Полученные значения помещены в таблице 2.
|
|
|
|
Таблица 2 |
|
|
|
|
|
|
|
Точки |
|
Координаты, см |
|||
x |
|
y |
|
z |
|
|
|
|
|||
А1 |
0,0 |
|
28,2 |
|
-6,7 |
А2 |
- |
|
- |
|
- |
А3 |
4,0 |
|
28,2 |
|
0,0 |
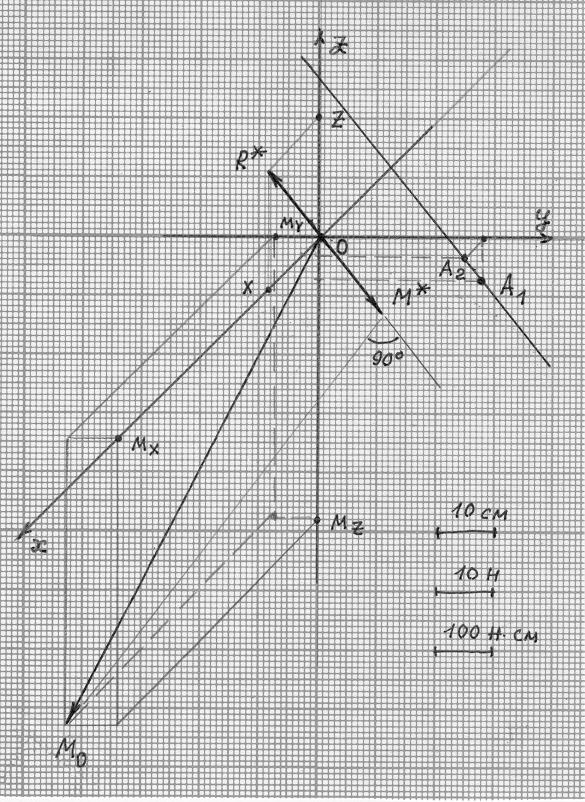
Рис. 2.
