
- •Введение
- •2.1.2. Основная программа анализатора
- •2.1.3. Вспомогательные процедуры
- •2.1.4. Распознающие процедуры
- •2.2. Умножение многочленов
- •2.2.1. Постановка задачи
- •2.2.2. Умножение и вывод
- •2.2.3. Транслятор многочленов
- •2.2.4. Обработка ошибок при трансляции
- •2.3. Табличный ll(1) – анализатор
- •2.4. Табличный транслятор многочленов
- •2.5. Реализация стека
- •2.6. Ll(1) – драйвер
- •3. Порядок выполнения работы
- •Варианты заданий
- •4. Контрольные вопросы
- •Список литературы
- •450000, Уфа - центр, ул. К. Маркса, 12
2.1.4. Распознающие процедуры
Для каждого нетерминала грамматики многочленов, т.е. для каждой синтаксической диаграммы (рис.1-3) запишем одну распознающую процедуру. Синтаксическая диаграмма для нетерминала «Многочлен» неудобна для программирования – она содержит цикл с выходом из середины. Заменим диаграмму эквивалентной, содержащей цикл с предусловием.
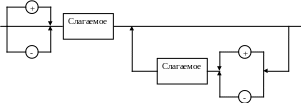
Рис.4. Преобразованная диаграмма «Многочлен»
Теперь можно записать распознающую процедуру. На диаграмме три последовательных участка – в процедуре три оператора, выполняемых один за другим: if, вызов процедуры Addend, цикл while.
procedure Polynom;
begin
if Ch in [‘+’, ‘-‘] then
NextCh;
Addend; {Слагаемое}
while Ch in [‘+’, ‘-‘] do begin
NextCh;
Addend;
end;
end;
Следующий нетерминал – «Слагаемое». Однако диаграмма, показанная на рис. 2, не разделяется на типовые фрагменты, что затрудняет программирование распознавателя. Неструктурированность обусловлена фрагментом, который помечен на рисунке знаком «?». Преобразуем диаграмму в эквивалентную, но состоящую только из совокупности типовых структур (рис.5). Для этого изобразим отдельно две ветви: одна соответствует слагаемому, начинающемуся с числа, другая – с буквы x. Фрагмент, выделенный на исходной диаграмме пунктирной рамкой, преобразуем в нетерминал «Степень».
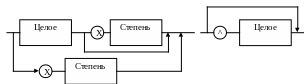
Рис. 5. Синтаксические диаграммы «Слагаемое» и «Степень»
Программирование распознающих процедур Addend (слагаемое) и Power (степень) теперь легко выполнить: диаграммы служат схемами алгоритма.
procedure Addend;
begin
if Ch = ‘x’ then begin
NextCh;
Power;
end
else begin
Number; {Целое}
if Ch = ‘x’ then begin
NextCh;
Power;
end;
end;
end;
procedure Power;
begin
if Ch = ‘^’ then begin
NextCh;
Number;
end;
end;
Последняя распознающая процедура – для «Целого». Ее также можно преобразовать, отделив блок, соответствующий первой цифре (обязательной), от остальных блоков.

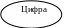
Рис.6. Синтаксическая диаграмма «Целое»
procedure Number;
begin
if Ch in [‘0’.. ‘9‘] then
NextCh
else
Error(‘Число начинается не с цифры’);
while Ch in [‘0’.. ‘9‘] do
NextCh;
end;
Распознаватель готов. Осталось только расположить процедуры в правильном порядке.
2.2. Умножение многочленов
2.2.1. Постановка задачи
Составим программу, вводящую в символьной форме два многочлена и выводящую их произведение в символьной форме в порядке убывания степеней.
Пример работы программы:
1-й многочлен:
3x^2+3x-5
2-й многочлен:
x^3-2x
Произведение:
3x^5+3x^4-11x^3-6x^2+10x
Приступим к решению поставленной задачи. Сформулируем общий план:
Напечатать заголовок.
Вывести текст первого многочлена, проанализировать его запись и преобразовать в удобную для дальнейших вычислений форму. Для выполнения действий с многочленами удобно хранить их в программе в виде массива коэффициентов, количество которых соответствует степени многочленов, а индекс каждого коэффициента равен степени соответствующего слагаемого.
Ввести текст второго многочлена, проанализировать его запись и преобразовать в удобную для дальнейших вычислений форму.
Перемножить многочлены.
Напечатать результат.
Запишем начало программы, в котором определим необходимые константы, типы данных и переменные.
program PolyMult;
const
nmax = 255; {Максимальная степень}
type
tPoly = record {Тип многочленов}
n: integer; {Степень}
a: array [0..nmax] of integer; {Коэффициенты}
end;
var
P1, P2, Q: tPoly; {Сомножители и произведение}
Теперь, пользуясь предварительно составленным планом, запишем основную программу.
begin
WriteLn (‘Перемножение многочленов’);
WriteLn;
WriteLn(‘Первый многочлен’);
GetPoly(P1);
WriteLn(‘Второй многочлен’);
GetPoly(P2);
MultPoly(P1, P2, Q); {Перемножение}
WriteLn;
WriteLn(“Произведение’);
WritePoly (Q); {Печать результатов}
WriteLn;
end.
