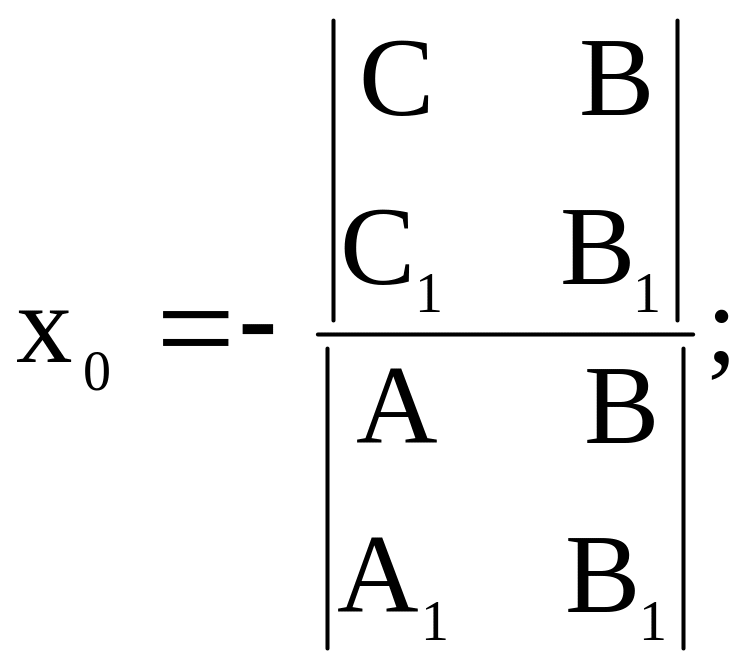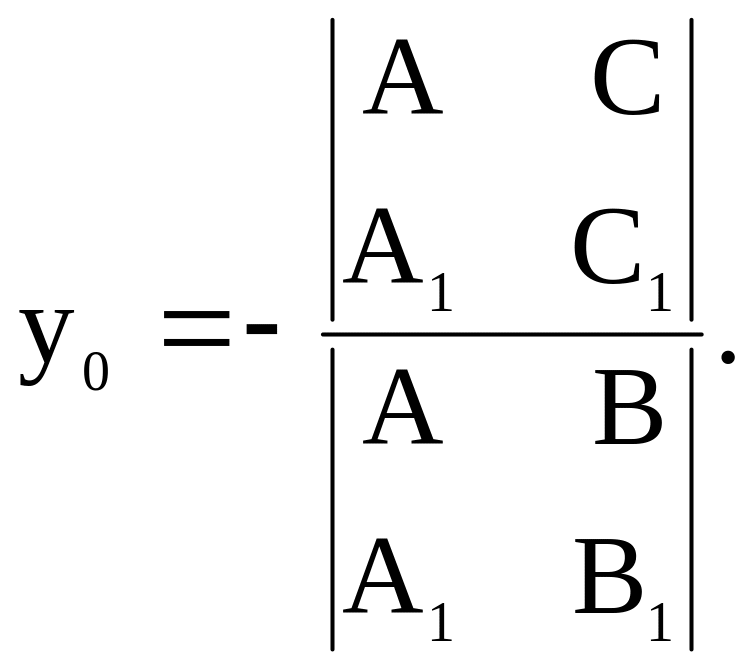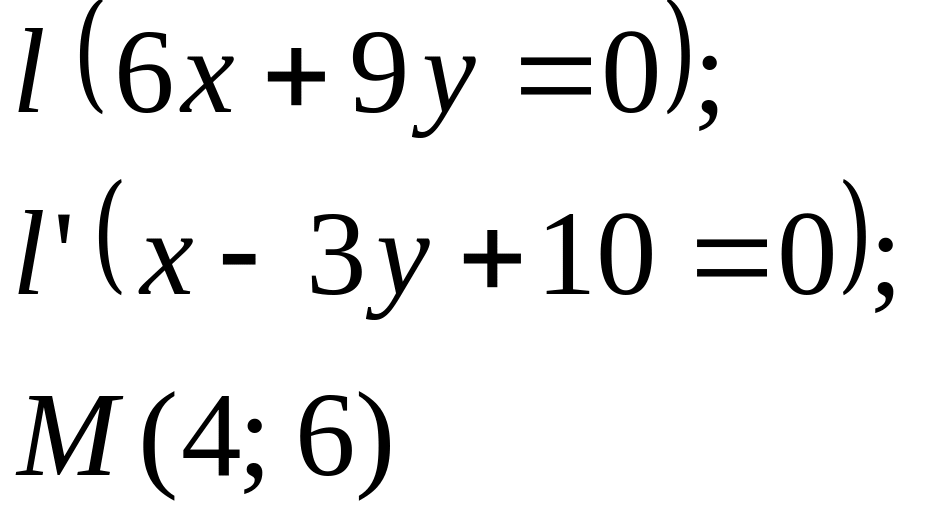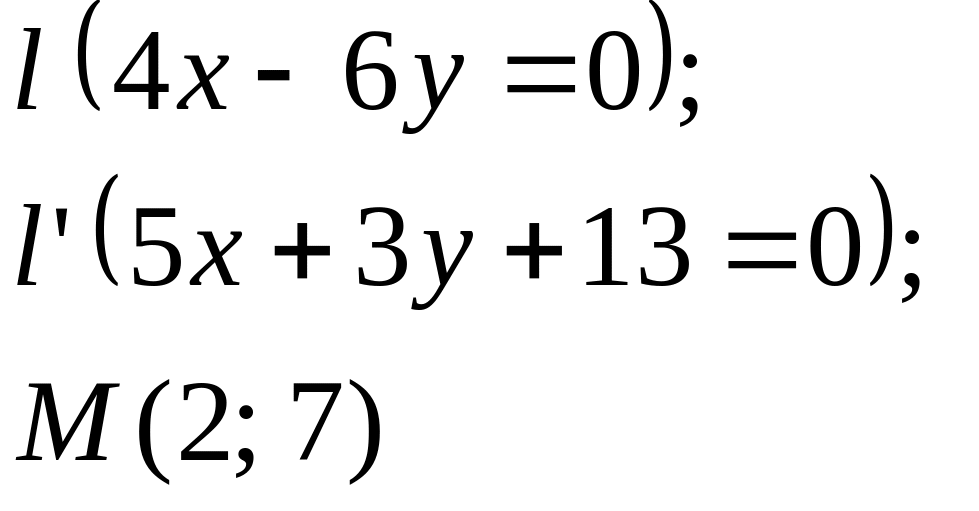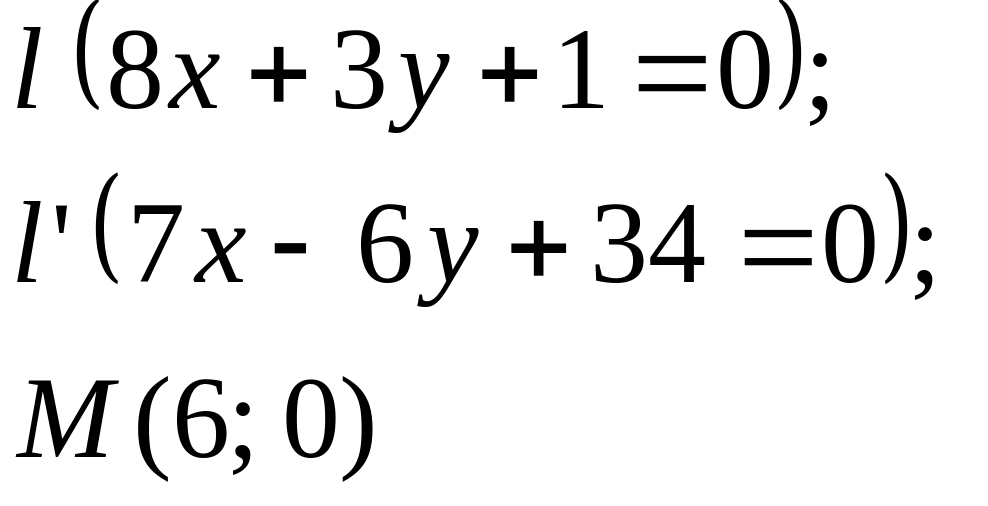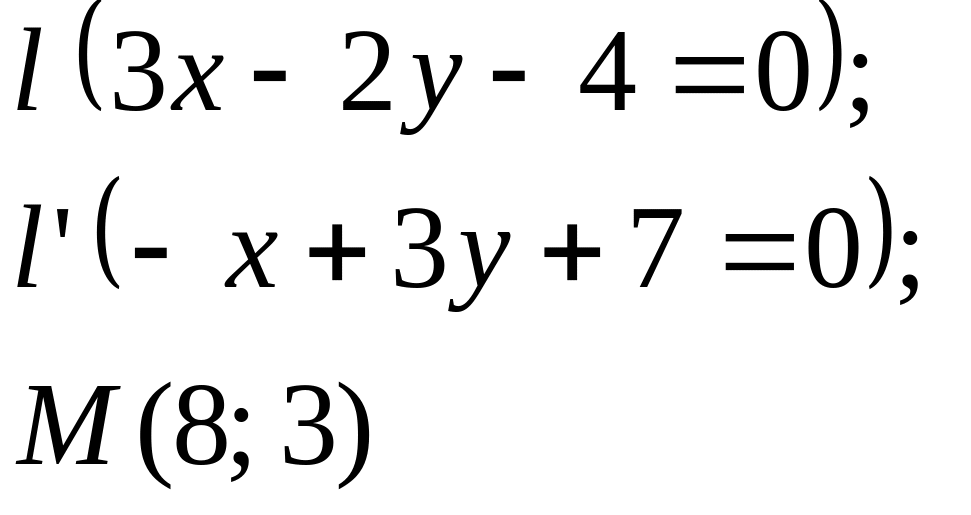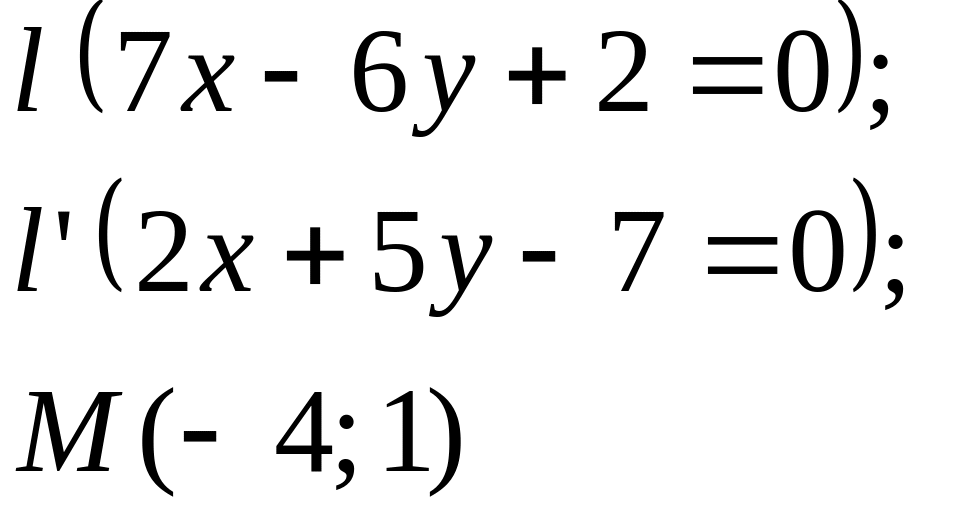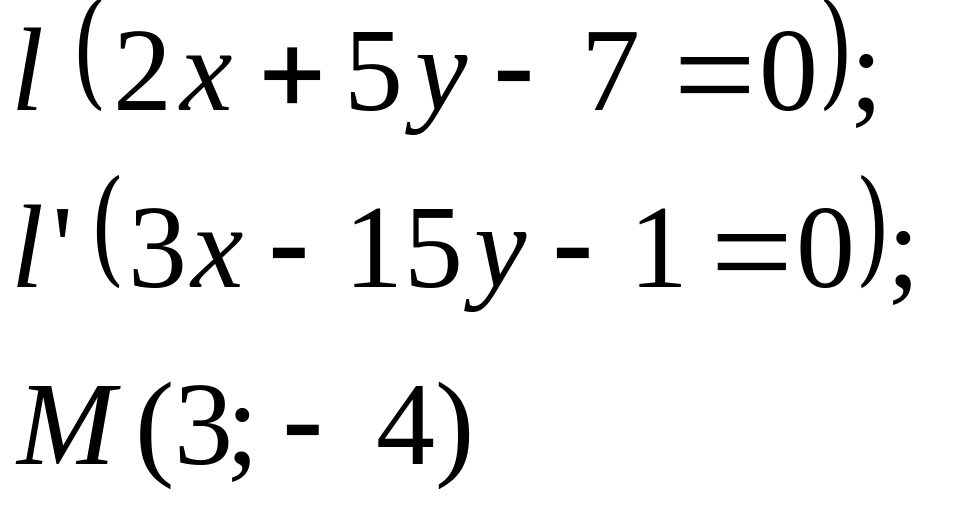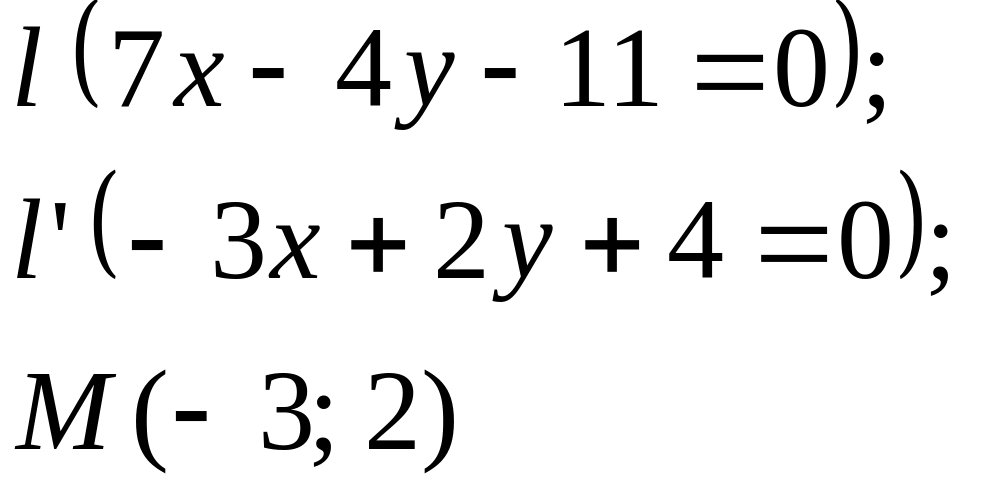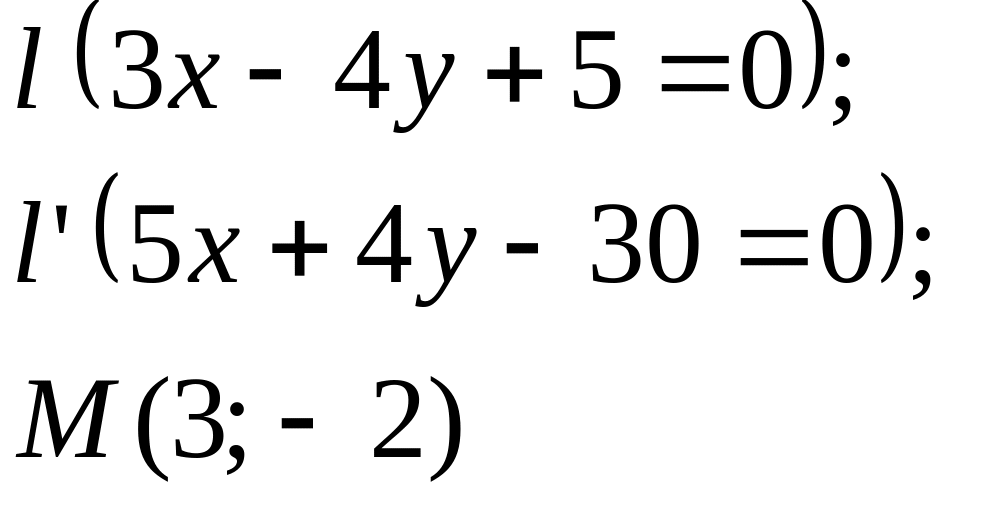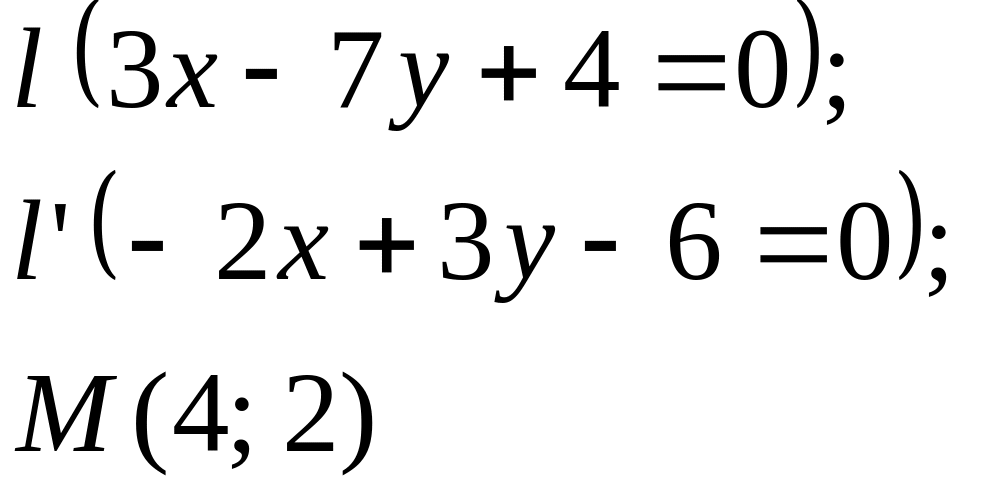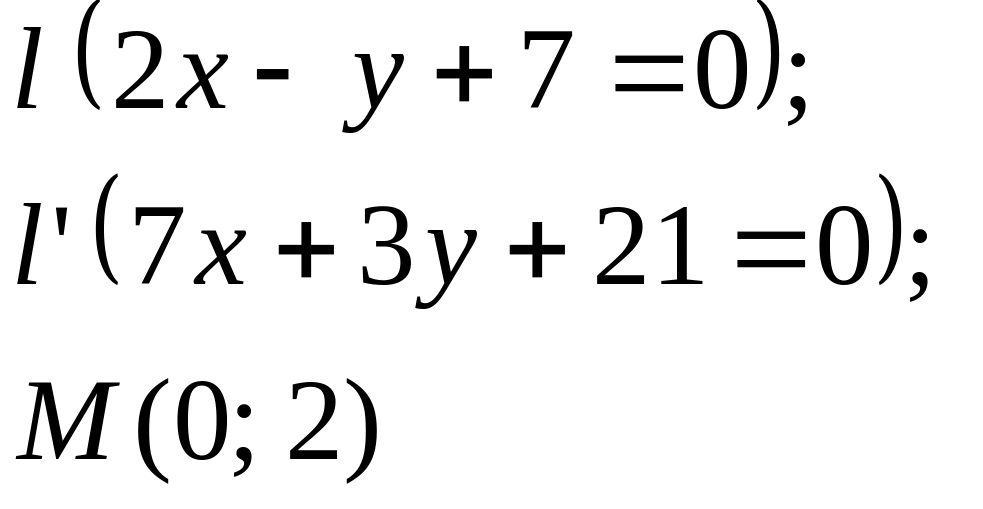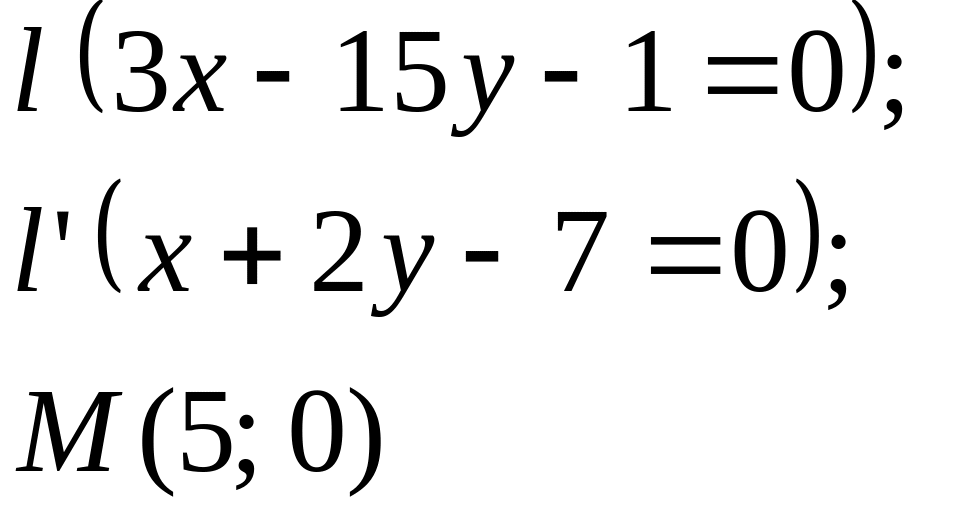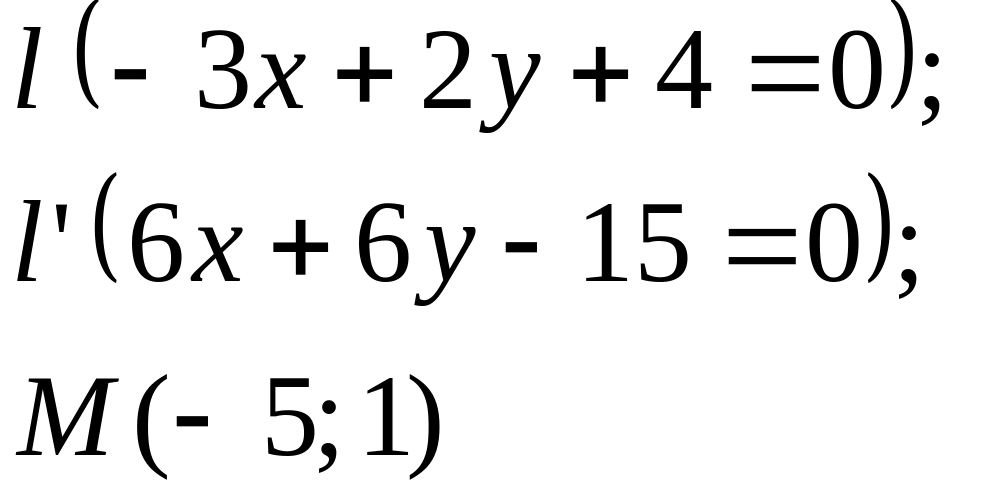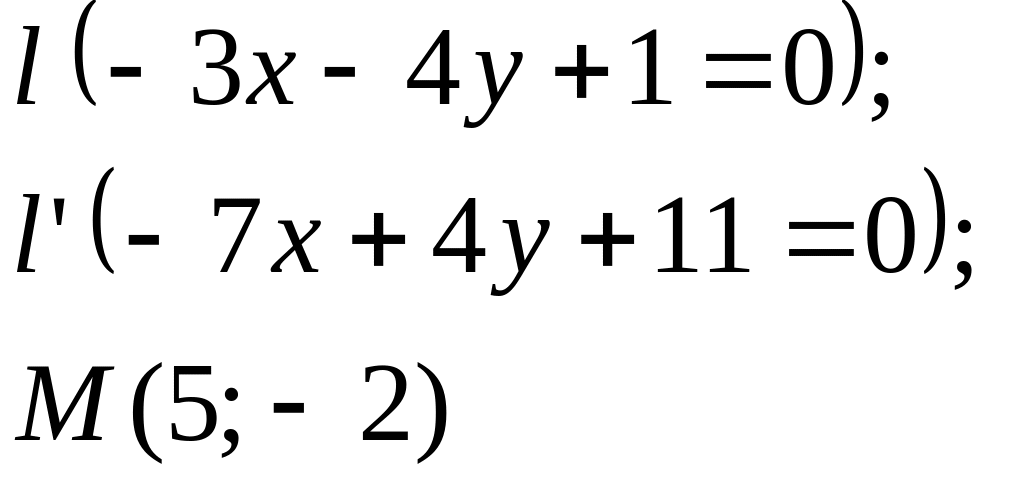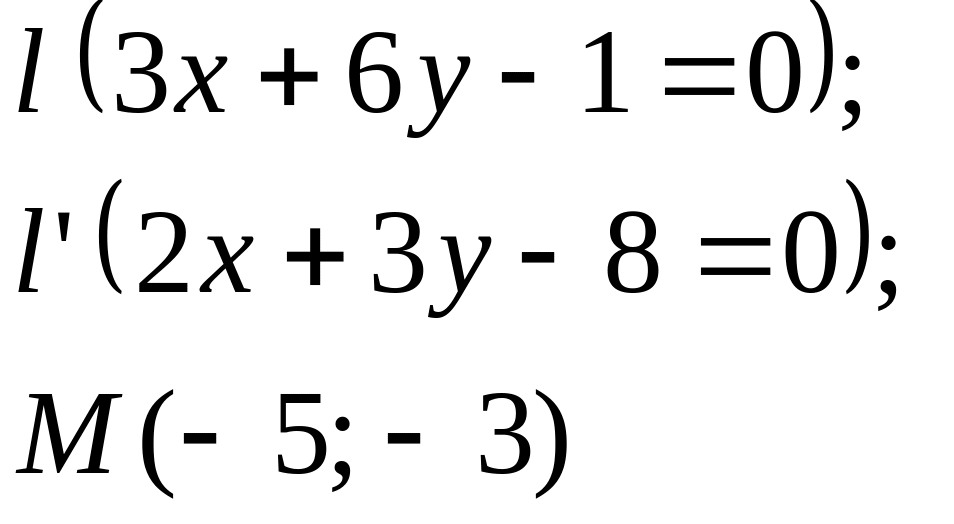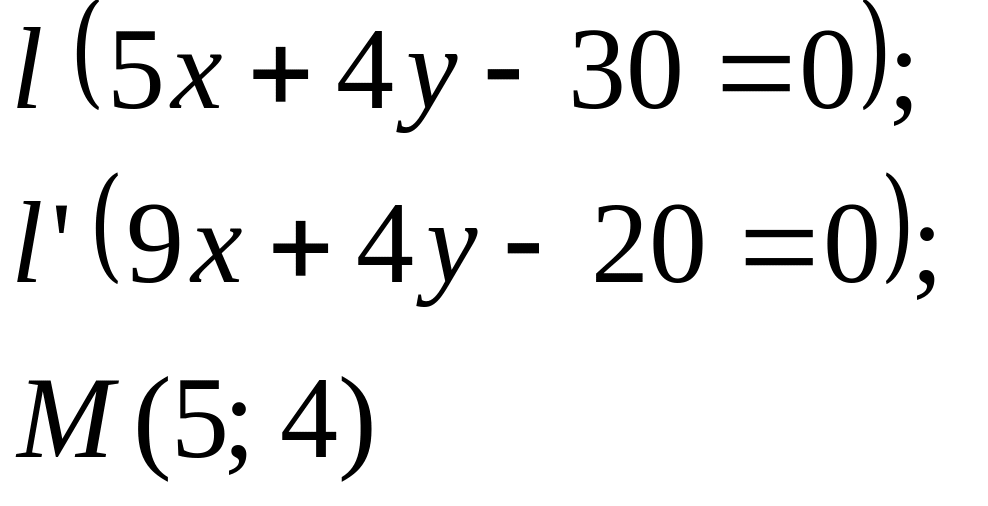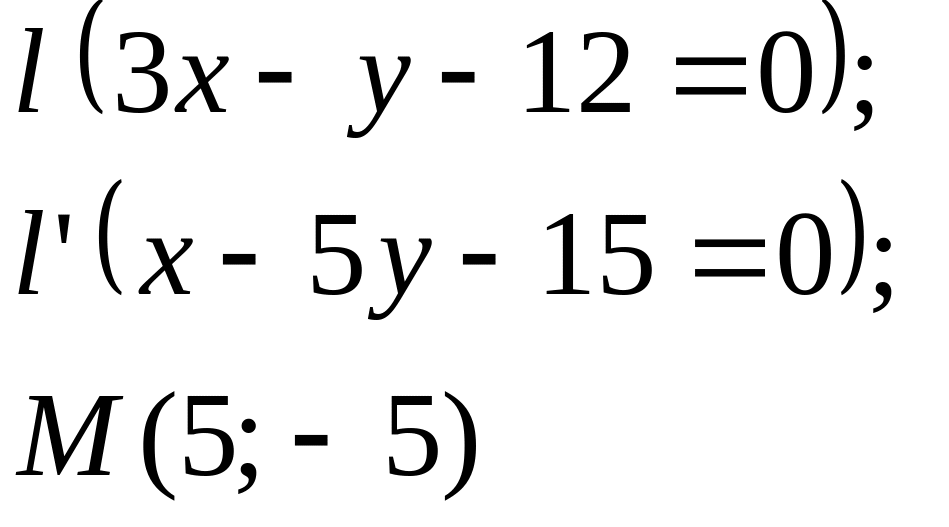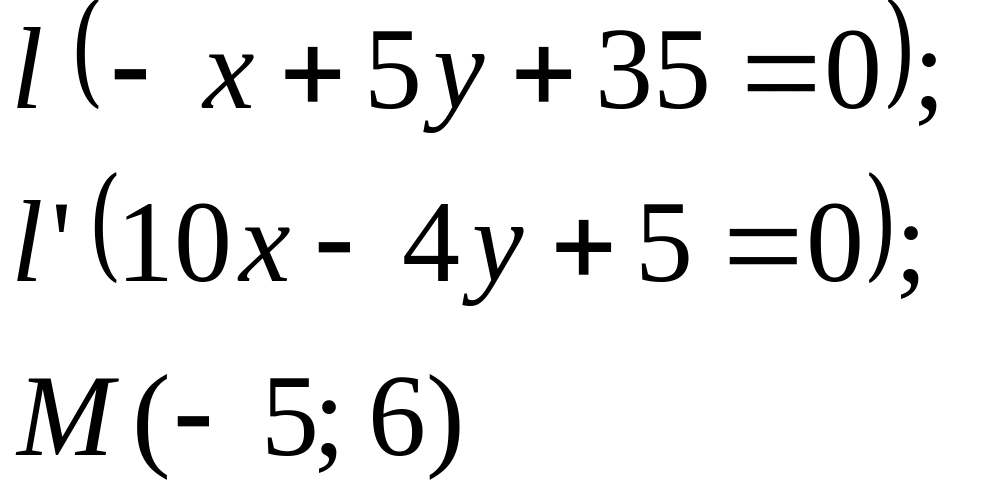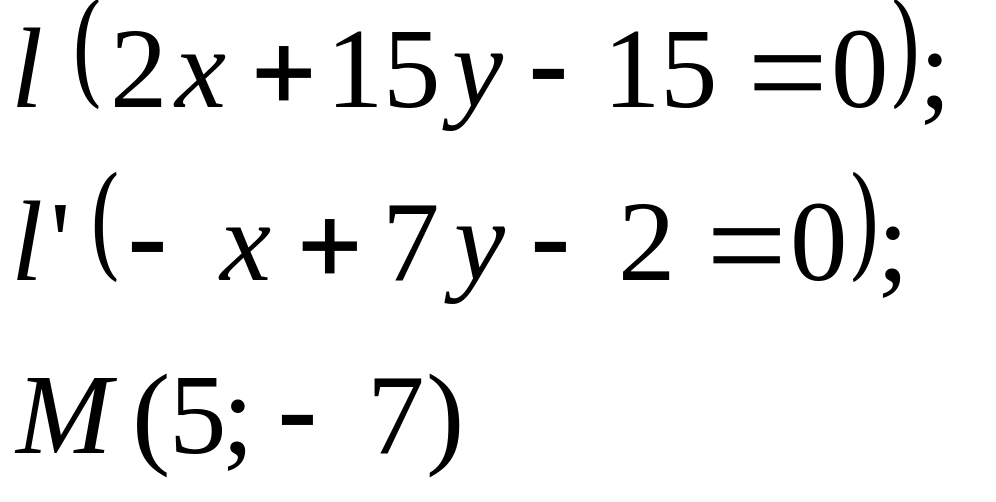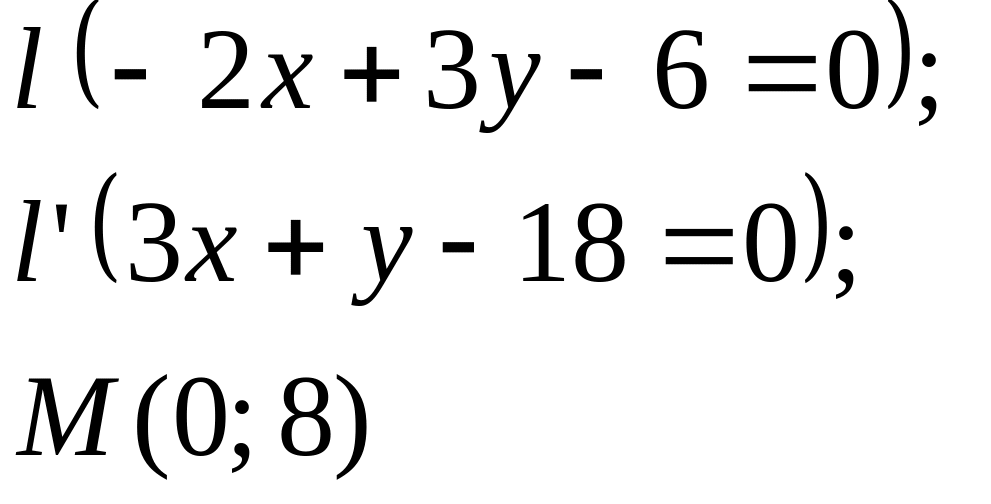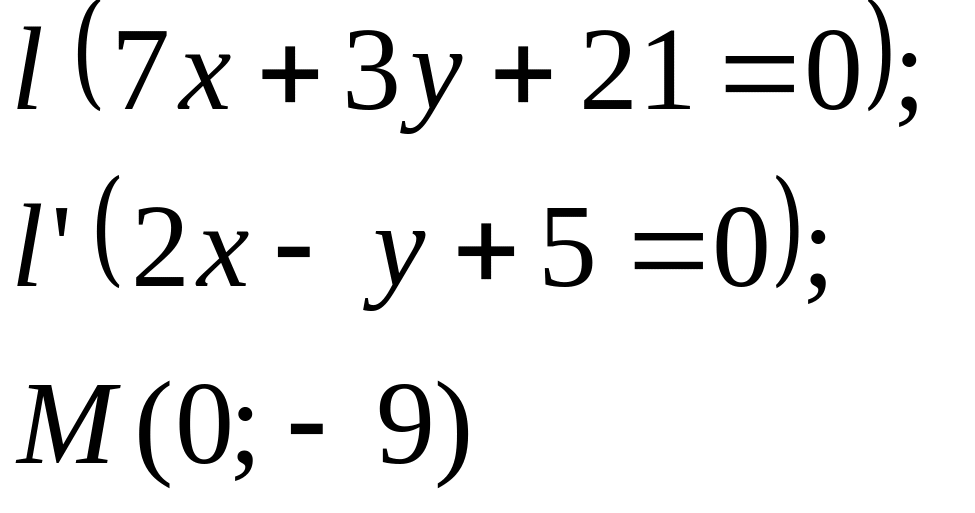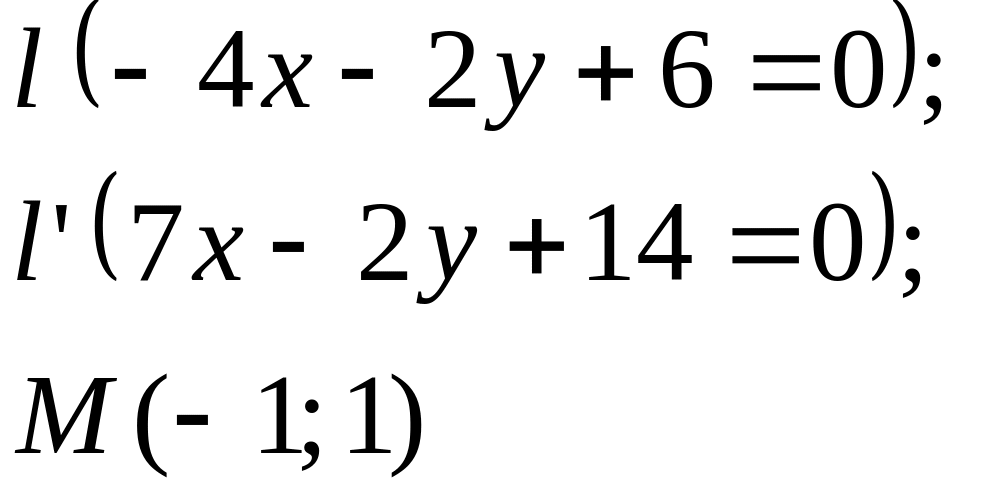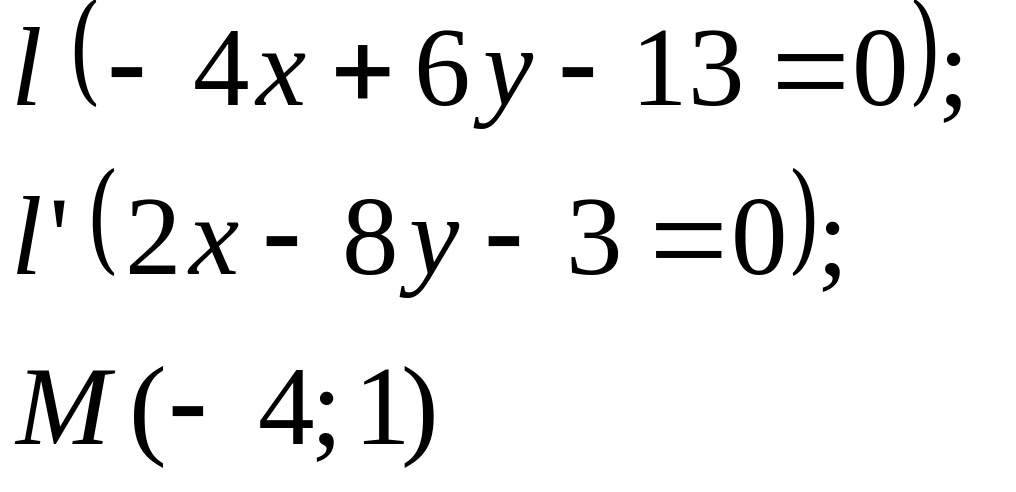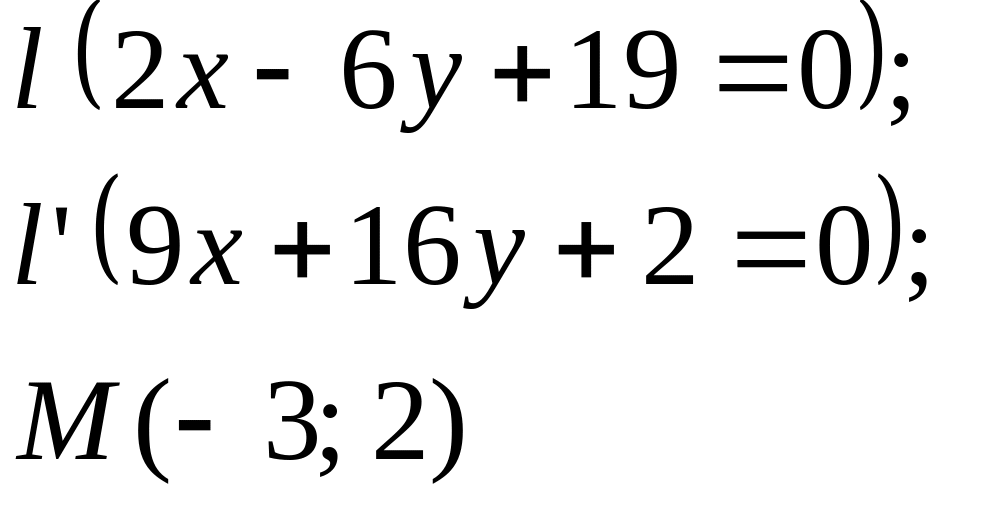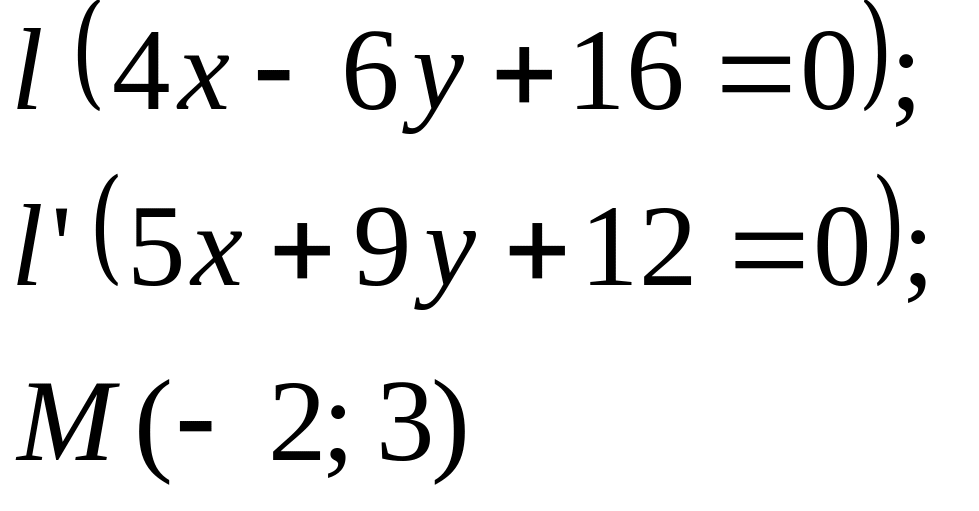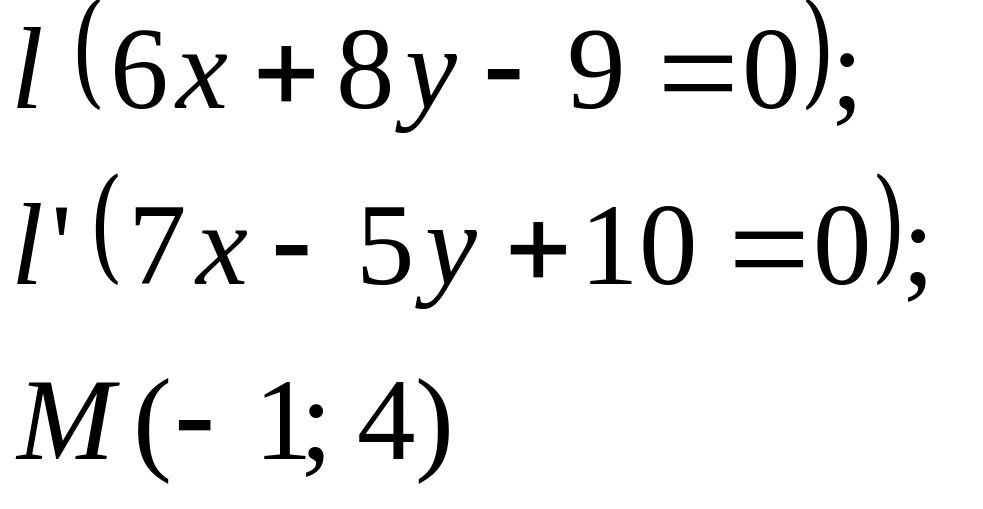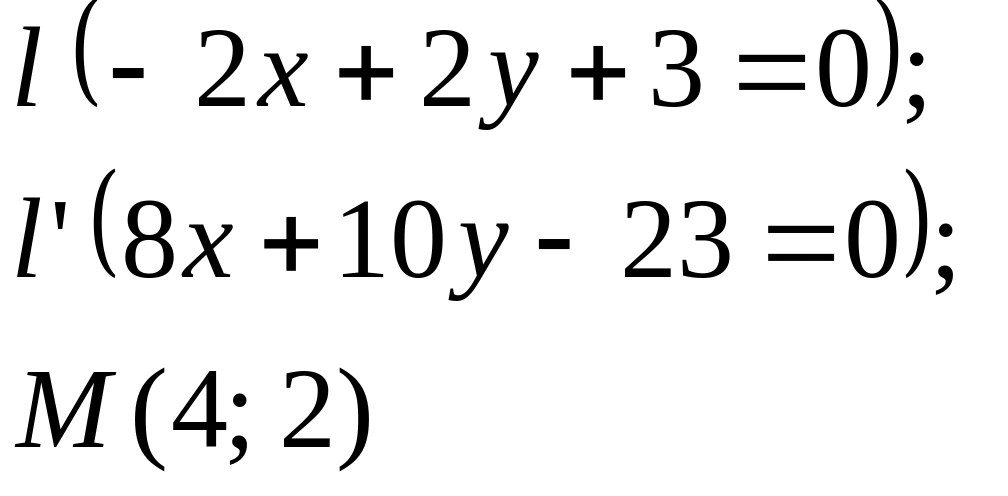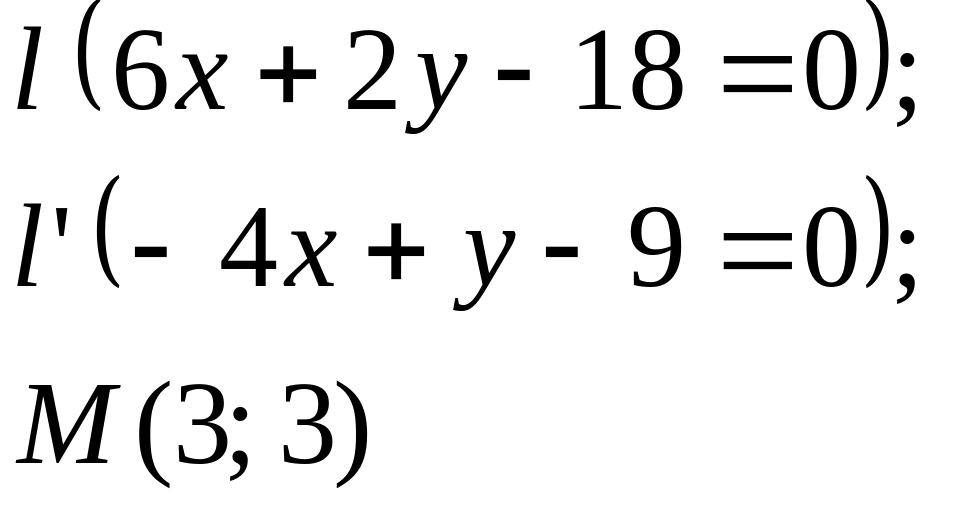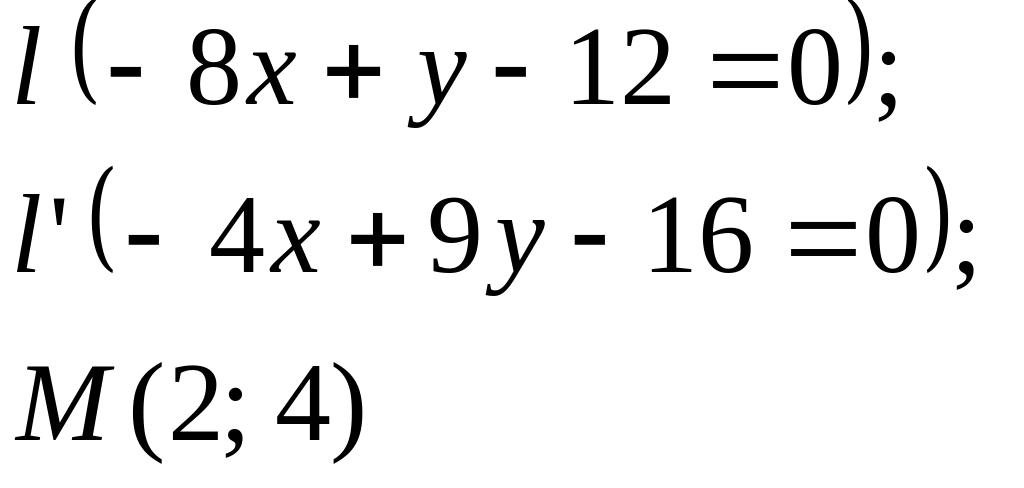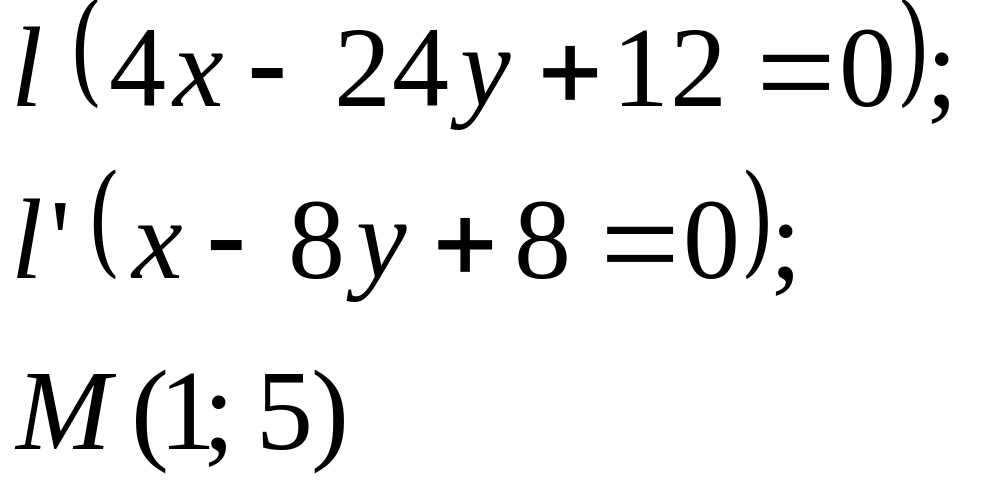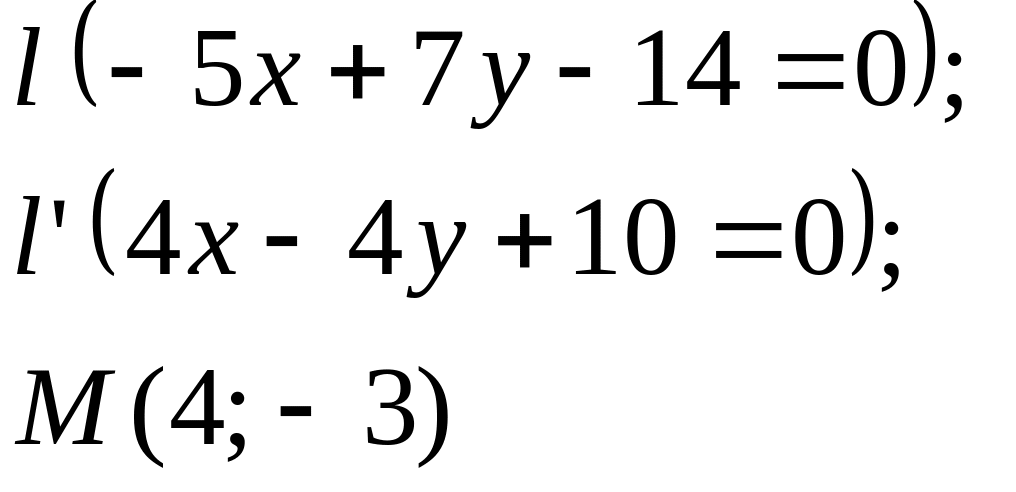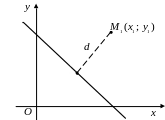
2.3. Расстояние от точки до прямой
Рис. 5 |
Расстояние d
от точки
|
до прямой Ax
+ By
+ C
= 0 (рис. 5)
вычисляется по формуле:
.
(16)
2.4. Пучок прямых
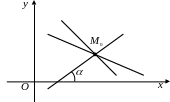
Через одну фиксированную точку (рис. 6) на плоскости можно провести бесконечное множество прямых. Это множество называется цент-ральным пучком (пучком) прямых, а точка называется центром пучка. Каждую из прямых пучка (кроме той, которая параллельна оси
ординат) можно представить уравнением:
|
(17) |
где tg – угловой коэффициент прямой (см. рис. 6).
Уравнение вида
(17) называется уравнением пучка
прямых
с центром в точке
|
Рис. 6 |
2.5. Угол между прямыми
Если пара прямых
на плоскости задана общими уравнениями:
(рис. 7, прямая f)
и
|
Рис. 7 |
(рис. 7, прямая g),
то косинус угла между этими прямыми
может быть вычислен по формуле:
|
(18) |
Если пара прямых
на плоскости задана уравнениями «с
угловым коэффициентом»:
и
,
то тангенс угла между этими прямыми
рассчитывается по уравнению:
tg |
(19) |
Если пара прямых
на плоскости задана своими каноническими
уравнениями:
и
то косинус угла между этими прямыми
определяется по формуле:
|
(20) |
2.6. Условия параллельности и перпендикулярности прямых
Прямые, заданные
общими уравнениями:
и
взаимно перпендикулярны тогда и только
тогда, когда
Данные прямые параллельны тогда и только
тогда, когда
Прямые на плоскости,
заданные в виде:
и
перпендикулярны только том случае,
когда
(при
).
Данные прямые параллельны тогда и только
тогда, когда их угловые коэффициенты
равны, т. е.
Прямые, заданные
своими каноническими уравнениями:
и
взаимно перпендикулярны тогда и только
тогда, когда
Данные прямые параллельны, если только
выполнено условие:
2.7. Точка пересечения непараллельных прямых
Если на плоскости
заданы две прямые:
и
,
то согласно утверждению 2 координаты
точки пересечения этих прямых можно
вычислить по формулам:
|
(21) |
|
(22) |
Задания для самостоятельной работы
3.1. Варианты типового расчета «Прямая на плоскости»
Задание 1. Указать особенности в расположении прямых на плоскости (прямая общего положения, проходящая или не проходящая через начало координат; прямая, параллельная оси Ох или Оу) и сделать чертеж. Уравнения заданных прямых по вариантам представлены в табл. 1.
Таблица 1
Данные к заданию 1
Вариант |
Данные прямые |
Вариант |
Данные прямые |
1 |
2 |
3 |
4 |
1 |
а)
в)
|
2 |
а)
в)
|
3 |
а)
в)
|
4 |
а)
в)
|
5 |
а)
в)
|
6 |
а)
в)
|
7 |
а)
в)
|
8 |
а)
в) |
9 |
а)
в)
|
10 |
а)
в)
|
11 |
а)
в)
|
12 |
а)
в)
|
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
Окончание табл. 1
1 |
2 |
3 |
4 |
13 |
а)
в)
|
14 |
а)
в)
|
15 |
а)
в)
|
16 |
а)
б)
в)
|
17 |
а)
в)
|
18 |
а)
в)
|
19 |
а)
в) |
20 |
а)
в)
|
21 |
а)
в)
|
22 |
а)
в)
|
23 |
а)
в)
|
24 |
а)
в)
|
25 |
а)
в)
|
26 |
а)
в)
|
27 |
а)
в)
|
28 |
а)
в)
|
29 |
а)
в)
|
30 |
а)
в)
|
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
Задание 2. Выбрать из имеющегося списка прямых на плоскости (табл. 2) пары: а) пересекающихся прямых; б) совпадающих прямых; в) прямых, не имеющих общих точек.
Таблица 2
Данные к заданию 2
Вариант |
Данные прямые |
Вариант |
Данные прямые |
1 |
2 |
3 |
4 |
1 |
4)
5)
|
2 |
4)
5)
|
3 |
1)
2)
3)
4)
5)
|
4 |
1)
2)
3)
4)
5)
|
5 |
1)
2)
3) 4)
5)
|
6 |
1)
2)
3)
4)
5)
|
7 |
1)
2)
3)
4)
5)
|
8 |
1)
2)
3)
4)
5)
|
9 |
1)
2) 3)
4)
5)
|
10 |
1)
2)
3)
4)
5)
|
3)
3)
Продолжение табл. 2
1 |
2 |
3 |
4 |
11 |
1) 2)
3)
4)
5)
|
12 |
1)
2)
3)
4)
5)
|
13 |
1)
2)
3)
4)
5)
|
14 |
1)
2)
3)
4)
5)
|
15 |
1)
2)
3)
4)
5)
|
16 |
1)
2)
3)
4)
5)
|
17 |
1)
2) 3)
4)
5)
|
18 |
1)
2)
3)
4)
5)
|
19 |
1)
2)
3)
4)
5)
|
20 |
1)
2)
3) 4)
5)
|
Окончание табл. 2
1 |
2 |
3 |
4 |
21 |
1)
2)
3)
4)
5)
|
22 |
1)
2)
3)
4)
5)
|
23 |
1)
2)
3)
4)
5)
|
24 |
1)
2)
3)
4)
5)
|
25 |
1)
2) 3)
4)
5)
|
26 |
1)
2)
3)
4)
5)
|
27 |
1)
2)
3)
4)
5)
|
28 |
1)
2)
3)
4)
5)
|
29 |
1)
2)
3)
4)
5)
|
30 |
1)
2)
3)
4)
5)
|
Задание
3.
Две точки
на плоскости заданы координатами:
и
,
– некоторый угол (табл. 3). Составить: 1)
уравнение прямой на плоскости, проходящей
через точки
и
найти ее направляющие косинусы; 2)
уравнение прямой, проходящей через
точку
и образующей с осью абсцисс угол
.
Таблица 3
Данные к заданию 3
Ва-риант |
Данные |
Ва-риант |
Данные |
1 |
2 |
3 |
4 |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
45º |
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
26 |
|
27 |
|
28 |
|
30º
60º
45º
90º
75º
120º
135º
150º
30º
60º
45º
90º
75º
120º
135º
150º
30º
60º
90º
75º
120º
135º
150º
30º
60º
45º
90º
Окончание табл. 3
1 |
2 |
3 |
4 |
29 |
|
30 |
|
75º
120ºЗадание 4. Дано общее уравнение прямой (табл. 4), записать для нее следующие виды уравнений:
1) каноническое
2) параметрические
3) «с угловым
коэффициентом»
4) «в отрезках»
5) нормальное
Построить заданную прямую в системе координат хОу.
Таблица 4
Данные к заданию 4
Ва-риант |
Данные |
Ва-риант |
Данные |
Ва-риант |
Данные |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
Окончание табл. 4
1 |
2 |
3 |
4 |
5 |
6 |
25 |
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
Задание
5. Даны
прямые
и точка М
(табл. 5).
Составить
уравнения прямых, проходящих: 1) через
точку М
параллельно
прямой l;
2) через точку М
перпендикулярно
прямой l.
Найти угол
между прямыми
и
и расстояние d
от точки М
до
прямой l.
Таблица 5
Данные к заданию 5
Ва-риант |
Данные |
Ва-риант |
Данные |
Ва-риант |
Данные |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
Продолжение табл. 5
1 |
2 |
3 |
4 |
5 |
6 |
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
Задание 6. Отметить на координатной плоскости область решения системы линейных неравенств (табл. 6).
Таблица 6
Данные к заданию 6
Ва-ри-ант |
Система неравенств |
Ва-ри-ант |
Система неравенств |
Ва-ри-ант |
Система неравенств |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
